短波紅外波段具備全天時、全天候成像的優(yōu)良潛力，借助焦平面探測陣列在現(xiàn)代社會發(fā)揮著日益重要的作用。為了解決短波紅外成像系統(tǒng)的離焦問題以提升平臺適用性，可將波前編碼技術引入短波紅外波段。

據(jù)麥姆斯咨詢報道，近期，中電科五十四所和桂林電子科技大學的聯(lián)合科研團隊在《激光與光電子學進展》期刊上發(fā)表了以“基于波前編碼的擴展景深短波紅外成像系統(tǒng)”為主題的文章。該文章第一作者和通訊作者為中電科五十四所王偉。

本文將波前編碼引入短波紅外波段，相比常規(guī)的單一性評價標準，采用綜合離焦一致性和圖像可恢復性的復合標準，解決離焦對成像質(zhì)量的影響，對提升載荷的平臺適應性和環(huán)境適應性具有一定的參考價值。

基于波前編碼技術的景深延拓原理

波前編碼的基本原理如圖1所示。與常規(guī)成像系統(tǒng)相比，波前編碼在光瞳位置放置特殊設計的相位板，利用波前光程差的變化改變相位，依據(jù)一定的評價函數(shù)得到對離焦去敏的、具備一定相似性的中間模糊圖像，最后利用計算機圖像處理算法復原圖像。

點擴散函數(shù)描述光學系統(tǒng)對點光源的輸出響應，理想的點擴散函數(shù)近似能量集中的小支持域脈沖函數(shù)。在經(jīng)典光學理論中，光學成像過程是物空間目標和點擴散函數(shù)的卷積。波前編碼系統(tǒng)犧牲能量集中度以擴大點擴散函數(shù)支持域，從而降低系統(tǒng)對離焦的敏感度。

光學傳遞函數(shù)取模運算即為調(diào)制傳遞函數(shù)，調(diào)制傳遞函數(shù)取平方即為點擴散函數(shù)，這兩個函數(shù)均與離焦參數(shù)Ψ無關，僅與相位板參數(shù)α有關，即波前編碼系統(tǒng)表現(xiàn)出良好的調(diào)制傳遞函數(shù)一致性或點擴散函數(shù)一致性。這是波前編碼的理論基礎，據(jù)此可以用同一圖像處理算法復原圖像，波前編碼系統(tǒng)的設計可簡化為對相位板參數(shù)的優(yōu)化。

短波紅外波前編碼系統(tǒng)設計與仿真

短波紅外光學系統(tǒng)優(yōu)化

為驗證波前編碼的有效性，對一臺輕小型大視場短波紅外相機進行優(yōu)化，采用25 μm像元尺寸InGaAs焦平面探測器，以空間頻率表示的極限分辨率（即單位長度能夠分辨的黑白線對數(shù)）約為20 lp/mm。光學系統(tǒng)指標參數(shù)如表1所示。

表1 光學系統(tǒng)指標參數(shù)

波前編碼相位板通常放置在系統(tǒng)光瞳位置，光學系統(tǒng)初始結構采用如圖2（a）所示的準對稱平場雙高斯物鏡，可以消除軸向像差。依據(jù)設計指標對初始結構進行調(diào)整，按照0.6的比例因子將初始結構縮放到指定焦距，更改初始系統(tǒng)的工作波長、通光孔徑、視場角。在保證像質(zhì)的前提下，綜合考慮玻璃材料的光學、熱力學等理化性質(zhì)，選擇透過率高和熱膨脹系數(shù)低的ZnSe和BaF?材料。

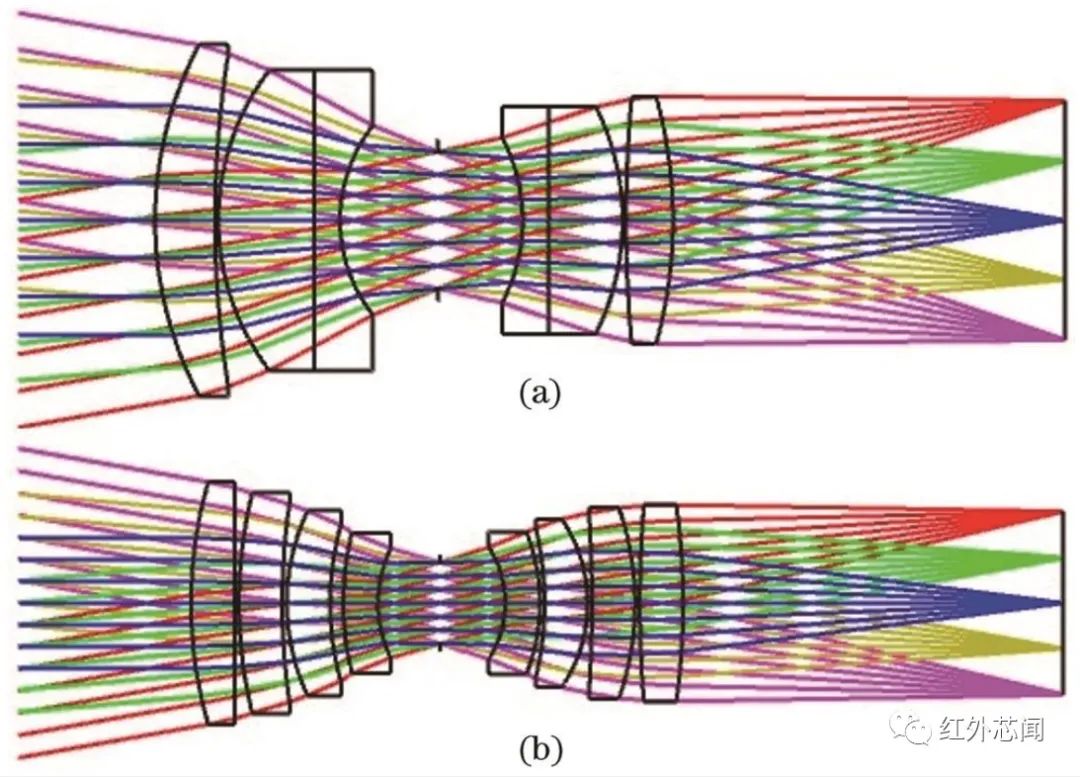
圖2 光學系統(tǒng)結構示意圖：（a）初始結構；（b）優(yōu)化后的結構

利用幾何光線追跡理論和阻尼最小二乘法對初始結構進行迭代優(yōu)化，優(yōu)化后的光學系統(tǒng)如圖2（b）所示，最佳焦面后截距為44.003 mm，光闌前后預留7.193 mm和7.523 mm用于安置相位板。分離膠合透鏡以增加光學設計自由度，提高對像差的控制能力，相較于雙膠合透鏡無需嚴格地匹配光焦度，適度增大空氣間隔以減小欠校正像差。適度增加前組中高折射率ZnSe透鏡光焦度，減輕低折射率BaF?透鏡光焦度負擔，避免曲率半徑過小。將前后組中的BaF?透鏡分裂為兩個透鏡以避免透鏡中心厚度過大。離軸視場光線沿徑向位置的焦點偏離焦平面產(chǎn)生場曲和像散，在焦面一側添加場鏡校正場曲和像散。

圖3為0°中心視場下光學系統(tǒng)在不同離焦參量下的調(diào)制傳遞函數(shù)曲線。其中，子午面和弧矢面函數(shù)值取平均。可以看出，在理想焦平面位置，在截止頻率范圍內(nèi)像質(zhì)良好，調(diào)制傳遞函數(shù)曲線接近衍射極限。隨著像面偏離理想焦平面，調(diào)制傳遞函數(shù)曲線迅速衰落，相同倍率下正向和負向離焦變化趨勢相同。在±5倍景深（±0.208 mm）離焦下，調(diào)制傳遞函數(shù)曲線迅速降低；在±10倍景深（±0.416 mm）離焦下，調(diào)制傳遞函數(shù)曲線出現(xiàn)零點，導致信息丟失和對比度反轉；在±15倍景深（±0.624 mm）和±20倍景深（±0.832 mm）離焦下，調(diào)制傳遞函數(shù)曲線零點依次增多。

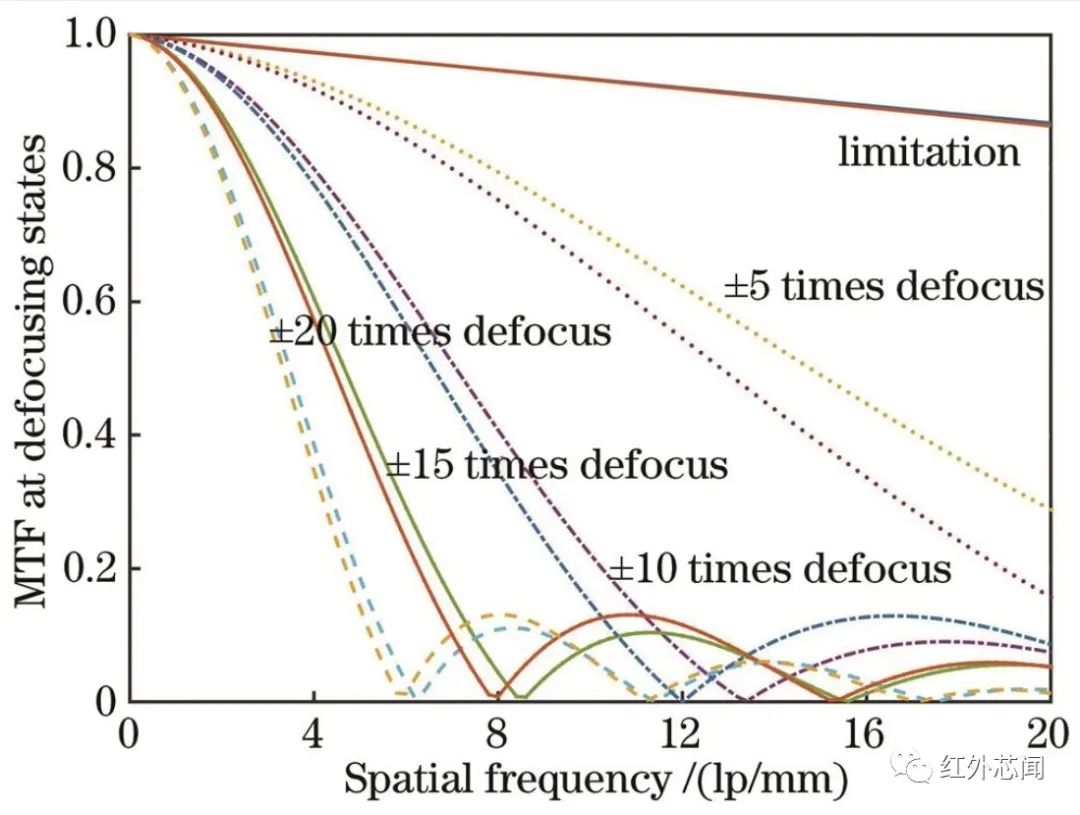
圖3 不同離焦狀態(tài)下的光學系統(tǒng)調(diào)制傳遞函數(shù)曲線

波前編碼系統(tǒng)優(yōu)化設計

在保持短波紅外光學系統(tǒng)不變的基礎上，在光闌位置插入特殊設計的三次方型相位板降低系統(tǒng)離焦敏感性。三次方型相位板采用2 mm厚度硅基玻璃材料制作，中心波長1.3 μm處折射率為1.598。采用擴展多項式面型模擬相位板前表面，相位板后表面采用標準平面，孔徑光闌置于后表面。

常規(guī)相位板參數(shù)優(yōu)化通常采用單一評價標準，缺乏對模糊圖像可恢復性的討論。依據(jù)前述卷積成像理論，成像過程是物空間目標與點擴散函數(shù)的卷積，圖像復原過程是低通濾波過程，點擴散函數(shù)的中心點能量決定了系統(tǒng)的信噪比，近似等于調(diào)制傳遞函數(shù)曲線與坐標軸包圍的面積。為了獲得足夠高的信噪比，需要對波前編碼系統(tǒng)點擴散函數(shù)的幅值加以約束。綜合考慮離焦一致性和圖像可恢復性，結合調(diào)制傳遞函數(shù)和點擴散函數(shù)關系，所采用的相位板參數(shù)優(yōu)化策略遵守以下兩條原則：1）截止頻率內(nèi)調(diào)制傳遞函數(shù)具備離焦一致性；2）全頻率內(nèi)點擴散函數(shù)幅值的能量相對集中。

光學設計軟件可以獲取不同離焦參量下離散空間頻率對應的調(diào)制傳遞函數(shù)值，圖4為不同徑向坐標系數(shù)下的波前編碼系統(tǒng)調(diào)制傳遞函數(shù)曲線變化趨勢圖，用以說明調(diào)制傳遞函數(shù)的離焦一致性，采用0°中心視場成像，依次對應±5、±10、±15、±20倍景深離焦。

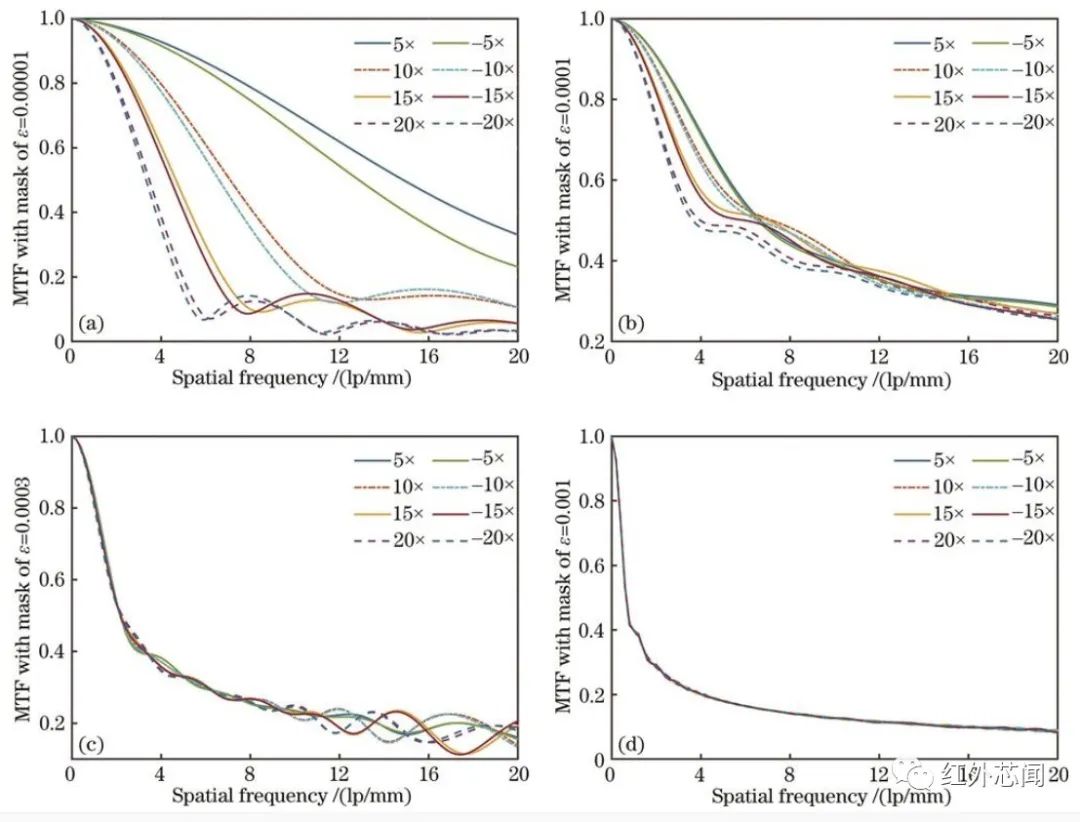
圖4 不同相位參數(shù)下波前編碼系統(tǒng)調(diào)制傳遞函數(shù)曲線

隨著徑向坐標系數(shù)的增加，調(diào)制傳遞函數(shù)的離焦一致性得到改善。在徑向坐標系數(shù)取極小值1×10??時，調(diào)制傳遞函數(shù)曲線出現(xiàn)不同程度的提升，函數(shù)零點導致的信息丟失和對比度反轉現(xiàn)象消失；在徑向坐標系數(shù)取1×10??時，調(diào)制傳遞函數(shù)曲線在0~10 lp/mm頻率范圍內(nèi)差異性顯著；這種差異性隨著徑向坐標系數(shù)的進一步增大向高頻方向轉移，徑向坐標系數(shù)取3×10??時，差異性主要集中在10~20 lp/mm頻率范圍內(nèi)；當徑向坐標系數(shù)高于1×10?3時，調(diào)制傳遞函數(shù)曲線趨向于一致，呈現(xiàn)出良好的離焦一致性。

為定量評價相位板參數(shù)，引入離散積分、歐氏距離、余弦相似性，分別用于表征調(diào)制傳遞函數(shù)的差異性和相似性。調(diào)制傳遞函數(shù)均為離散采樣點，利用矩形近似和極限原理計算定積分。離散積分準確性與采樣率相關，采樣間隔Δu取0.2 lp/mm。

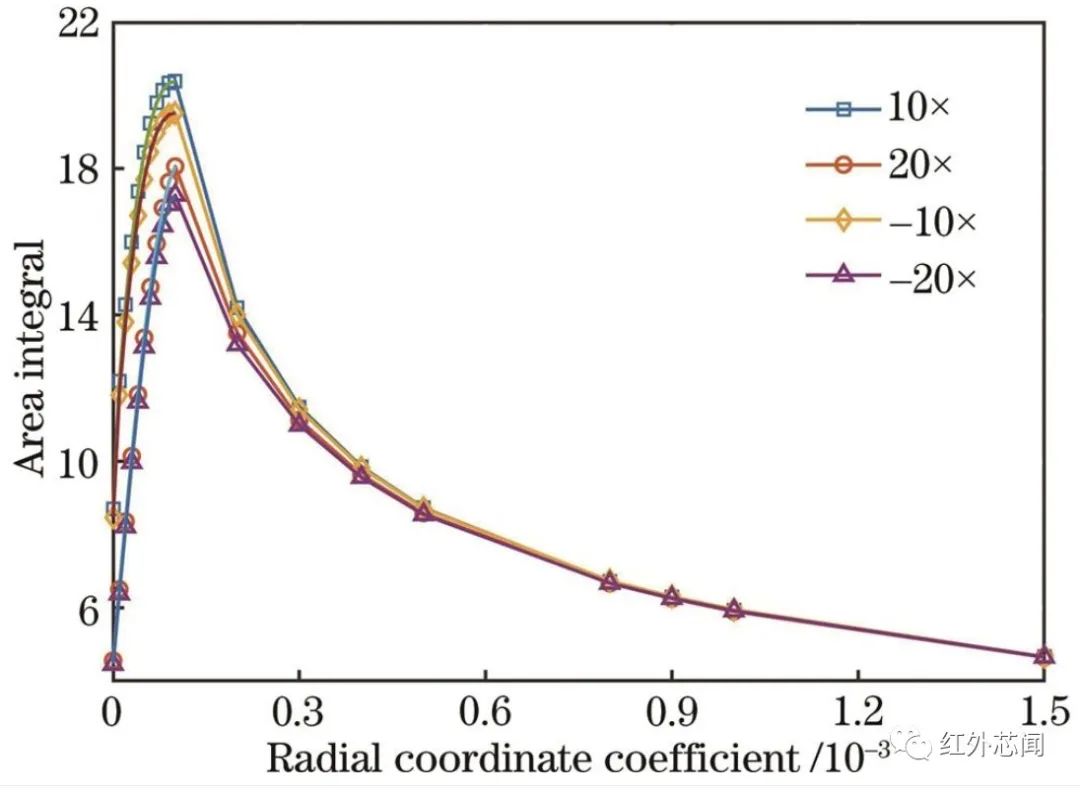
圖5 不同離焦狀態(tài)下的調(diào)制傳遞函數(shù)積分曲線

歐氏距離即歐幾里得度量，在一維空間中可以表征兩點之間的差異，與均方根誤差具有相似性和關聯(lián)性。

不同徑向坐標系數(shù)下，±10倍和±20倍景深離焦歐氏距離曲線如圖6所示，縱坐標取對數(shù)以直觀展示數(shù)據(jù)。理論上，差異顯著性與歐氏距離成反比，離焦一致性良好的調(diào)制傳遞函數(shù)具有相似的歐氏距離數(shù)值。隨著徑向坐標系數(shù)的增大，歐氏距離數(shù)值接近0，表明不同離焦參量下的調(diào)制傳遞具有良好的一致性。

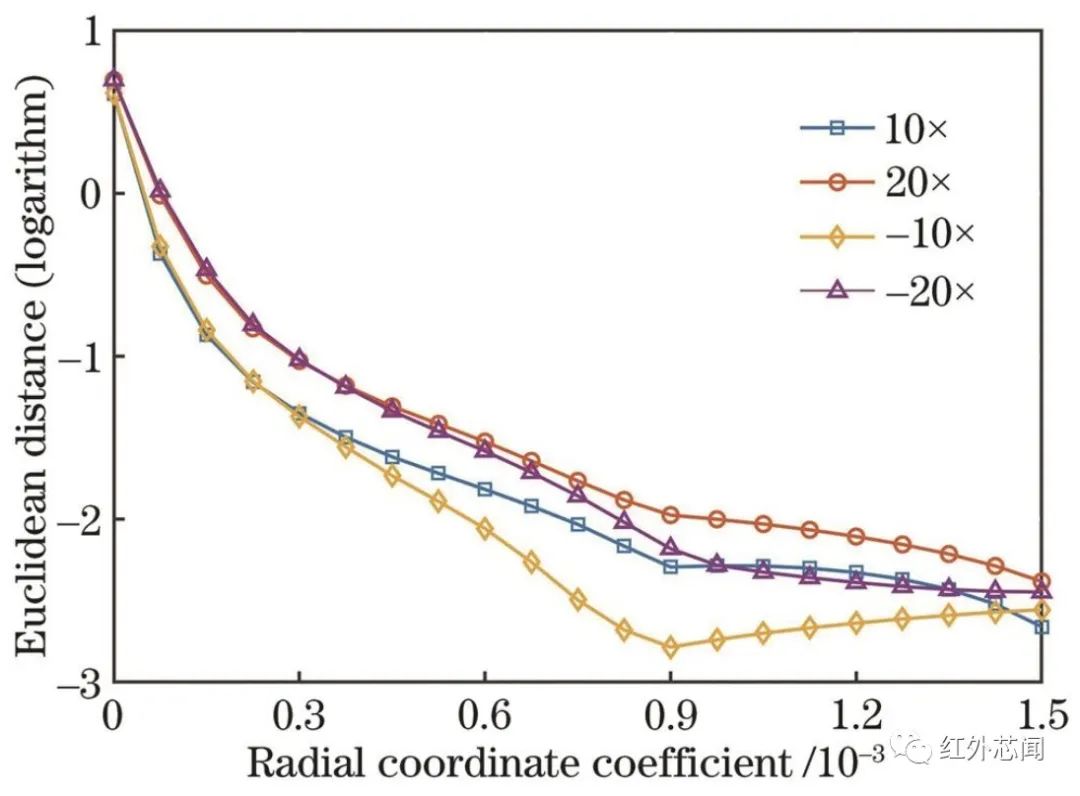
圖6 不同離焦狀態(tài)下的歐式距離曲線

余弦相似性通常用來表征二維空間中兩個向量之間夾角的余弦，余弦越接近于1，則向量的夾角越接近于0，即兩個向量越相似，該理論在多維空間中同樣適用。

不同徑向坐標系數(shù)下，±10倍和±20倍景深離焦下的余弦相似性曲線如圖7所示，為便于展示曲線細部差異，縱坐標采用差值處理。理論上離焦一致性良好的調(diào)制傳遞函數(shù)具有相似的夾角余弦數(shù)值，隨著徑向坐標系數(shù)的增大，夾角余弦逐漸變大，不同離焦參量下的夾角余弦差距逐漸縮小并接近1。

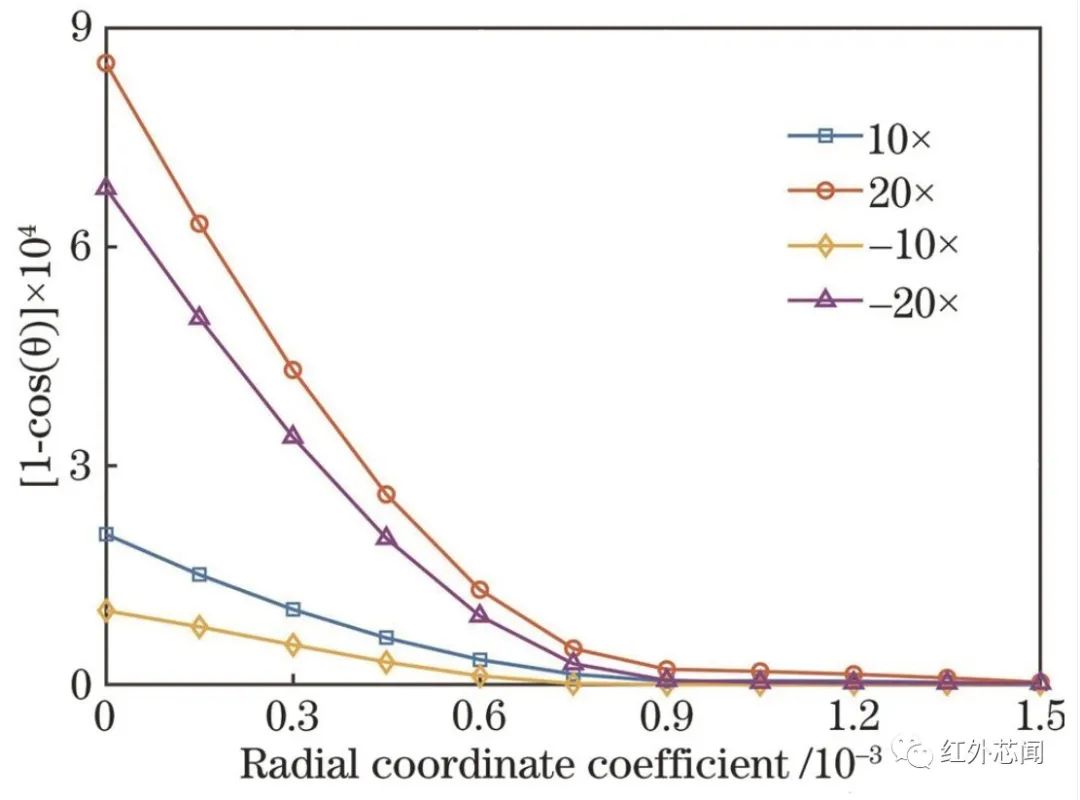
圖7 不同離焦狀態(tài)下的余弦相似性曲線

通過圖5~7的分析可知，點擴散函數(shù)中心能量取極值時，不同離焦倍率的調(diào)制傳遞函數(shù)差異顯著，因此徑向坐標系數(shù)的選擇應當在確保調(diào)制傳遞函數(shù)一致性的同時，盡可能保證點擴散函數(shù)中心能量的集中性。歐氏距離和余弦相似性分析表明，徑向坐標系數(shù)取1.5×10?3時，調(diào)制傳遞函數(shù)對離焦脫敏；離散積分分析表明，在此基礎上增大徑向坐標系數(shù)，調(diào)制傳遞函數(shù)包圍面積進一步減小。

優(yōu)化后的波前編碼系統(tǒng)0°視場角下的三維和二維笛卡兒坐標典型點擴散函數(shù)如圖8所示，縱坐標表征的點擴散函數(shù)強度歸一化到100。與脈沖型函數(shù)相比，波前編碼系統(tǒng)點擴散函數(shù)支持域變大，中心點能量相對較高，同時在第四象限集中了大部分能量。第四象限的能量呈三角形分布，以零點坐標為頂點，以水平坐標軸為直角邊，點擴散函數(shù)強度隨著與頂點距離的增加而變小，直角邊強度較象限內(nèi)強度高。考慮光學系統(tǒng)的視場，點擴散函數(shù)在邊緣視場約有3.5%~7.9%的能量損失。

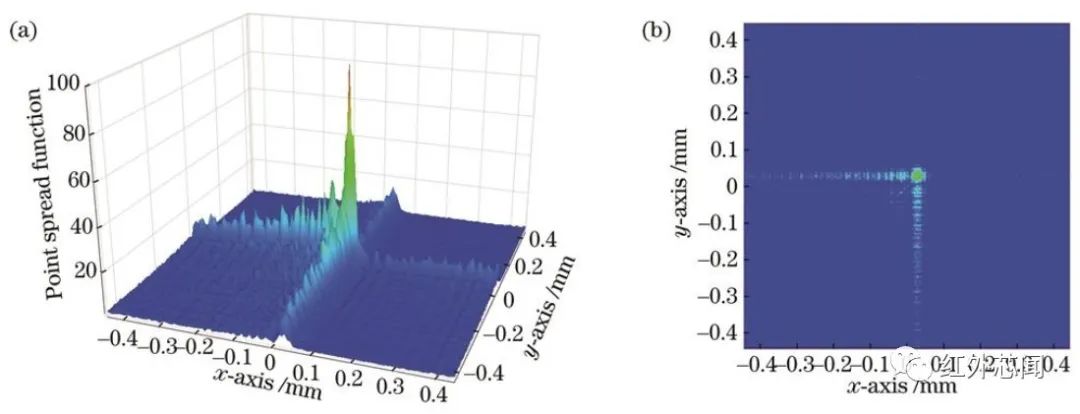
圖8 波前編碼系統(tǒng)點擴散函數(shù)

短波紅外波前編碼仿真

由于點擴散函數(shù)支持域的擴大化，波前編碼系統(tǒng)中間圖像是對離焦不敏感的模糊圖像。模糊圖像復原是波前編碼應用中的核心問題之一，通常采用低通濾波算法從模糊圖像中還原清晰圖像。

圖9為常規(guī)光學系統(tǒng)和波前編碼系統(tǒng)在不同離焦量下的成像效果對比圖。目標為北方地區(qū)冬季室外場景，圖像分辨率為640 pixel×512 pixel。由于正向離焦和反向離焦具有相似的成像效果，因此選擇0倍、10倍、20倍景深離焦。常規(guī)光學系統(tǒng)的成像質(zhì)量隨離焦的增加而惡化，大倍率離焦下調(diào)制傳遞函數(shù)零點丟失，導致信息無法還原。由于相位板對波前編碼系統(tǒng)光程差的改變，即使在理想焦面位置中間圖像仍然模糊，不同倍率離焦下系統(tǒng)具有相似的中間模糊圖像，中間模糊圖像灰度值差異在-0.071~0.082之間，均方根誤差為0.0132。

圖9 光學系統(tǒng)離焦效果示意圖：（a）（b）（c）常規(guī)光學系統(tǒng)；（d）（e）（f）波前編碼系統(tǒng)

在波前編碼低通濾波反卷積算法中，Lucy-Richardson算法是基于貝葉斯理論的空域圖像迭代復原算法，利用期望最大化實現(xiàn)復原圖像的最大似然性，適用于處理已知點擴散函數(shù)導致的圖像模糊。仿真實驗中從0倍離焦波前編碼系統(tǒng)的0°中心視場對應的圖像中選取點擴散函數(shù)卷積核，采用Lucy-Richardson經(jīng)典算法對圖像進行還原處理，波前編碼系統(tǒng)中間模糊圖像復原效果如圖10所示。0倍離焦、10倍離焦、20倍離焦復原圖像信噪比分別為6.57 dB、6.68 dB、6.66 dB，峰值信噪比分別為26.91 dB、38.50 dB、37.34 dB。統(tǒng)計結果與圖10相同，由于點擴散函數(shù)支持域的擴大化，點擴散函數(shù)中心點附近存在較強的能量起伏，復原圖像出現(xiàn)不同程度的振鈴現(xiàn)象，在0倍離焦下尤甚，表現(xiàn)為峰值信噪比的降低。

圖10 波前編碼系統(tǒng)復原圖像示意圖：（a）0倍離焦；（b）10倍離焦；（c）20倍離焦

結論

將波前編碼引入短波紅外波段，設計一款60 mm口徑、20°視場輕小型短波紅外相機，在系統(tǒng)光瞳處添加三次方型硅基相位板擴展景深。遵循調(diào)制傳遞函數(shù)一致性和點擴散函數(shù)中心點能量集中化兩大原則，擺脫常規(guī)的單一性評價指標，利用光學軟件優(yōu)化后的相位板參數(shù)為1.5×10?3。短波紅外圖像仿真結果表明，至少在±20倍景深范圍內(nèi)，波前編碼系統(tǒng)利用Lucy-Richardson經(jīng)典算法可以從中間模糊圖像中還原清晰圖像，峰值信噪比高達38.5038 dB。波前編碼僅對相位板參數(shù)進行優(yōu)化設計，保留了原始系統(tǒng)的功能完整性，對由離焦引起的成像質(zhì)量的惡化具有良好的校正作用，對提升載荷的平臺適應性和環(huán)境適應性具有一定的參考價值，后續(xù)可以在此基礎上探討波前編碼在初級像差校正和實際應用中的作用。

編輯：黃飛