這篇文章對(duì)轉(zhuǎn)置卷積(反卷積)有著很好的解釋?zhuān)@里將其翻譯為中文,以饗國(guó)人。
對(duì)于上采用的需求
當(dāng)我們用神經(jīng)網(wǎng)絡(luò)生成圖片的時(shí)候,經(jīng)常需要將一些低分辨率的圖片轉(zhuǎn)換為高分辨率的圖片。
對(duì)于這種上采樣(up-sampling)操作,目前有著一些插值方法進(jìn)行處理: 最近鄰插值(Nearest neighbor interpolation) 雙線(xiàn)性插值(Bi-Linear interpolation) 雙立方插值(Bi-Cubic interpolation) 以上的這些方法都是一些插值方法,需要我們?cè)跊Q定網(wǎng)絡(luò)結(jié)構(gòu)的時(shí)候進(jìn)行挑選。這些方法就像是人工特征工程一樣,并沒(méi)有給神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)的余地,神經(jīng)網(wǎng)絡(luò)不能自己學(xué)習(xí)如何更好地進(jìn)行插值,這個(gè)顯然是不夠理想的。
為什么是轉(zhuǎn)置卷積
轉(zhuǎn)置卷積(Transposed Convolution)常常在一些文獻(xiàn)中也稱(chēng)之為反卷積(Deconvolution)和部分跨越卷積(Fractionally-strided Convolution),因?yàn)榉Q(chēng)之為反卷積容易讓人以為和數(shù)字信號(hào)處理中反卷積混起來(lái),造成不必要的誤解,因此下文都將稱(chēng)為轉(zhuǎn)置卷積,并且建議各位不要采用反卷積這個(gè)稱(chēng)呼。 如果我們想要我們的網(wǎng)絡(luò)可以學(xué)習(xí)到最好地上采樣的方法,我們這個(gè)時(shí)候就可以采用轉(zhuǎn)置卷積。這個(gè)方法不會(huì)使用預(yù)先定義的插值方法,它具有可以學(xué)習(xí)的參數(shù)。理解轉(zhuǎn)置卷積這個(gè)概念是很重要的,因?yàn)樗谌舾芍匾奈墨I(xiàn)中都有所應(yīng)用,如: 1、在DCGAN中的生成器將會(huì)用隨機(jī)值轉(zhuǎn)變?yōu)橐粋€(gè)全尺寸(full-size)的圖片,這個(gè)時(shí)候就需要用到轉(zhuǎn)置卷積。 2、在語(yǔ)義分割中,會(huì)使用卷積層在編碼器中進(jìn)行特征提取,然后在解碼層中進(jìn)行恢復(fù)為原先的尺寸,這樣才可以對(duì)原來(lái)圖像的每個(gè)像素都進(jìn)行分類(lèi)。這個(gè)過(guò)程同樣需要用到轉(zhuǎn)置卷積。
卷積操作
讓我們回顧下卷積操作是怎么工作的,并且我們將會(huì)從一個(gè)小例子中直觀的感受卷積操作。假設(shè)我們有一個(gè)的矩陣,我們將在這個(gè)矩陣上應(yīng)用的卷積核,并且不添加任何填充(padding),步進(jìn)參數(shù)(stride)設(shè)置為1,就像下圖所示,輸出為一個(gè)的矩陣。
這個(gè)卷積操作在輸入矩陣和卷積核中,對(duì)每個(gè)元素的乘積進(jìn)行相加。因?yàn)槲覀儧](méi)有任何填充和使用1為步進(jìn),因此我們只能對(duì)這個(gè)操作進(jìn)行4次,因此我們的輸出矩陣尺寸為。
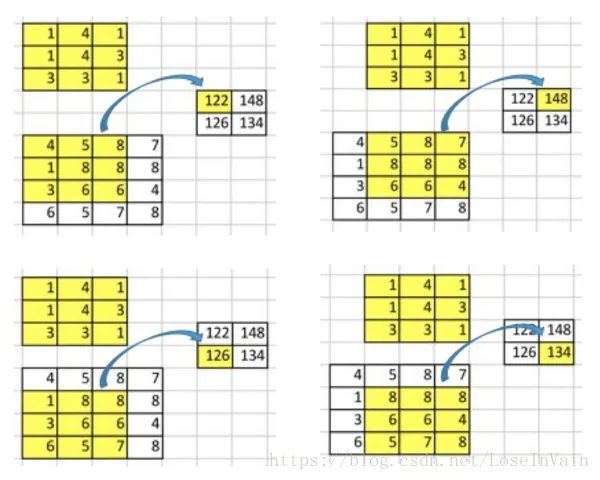
這種卷積操作使得輸入值和輸出值之間存在有位置上的連接關(guān)系,舉例來(lái)說(shuō),輸入矩陣左上方的值將會(huì)影響到輸出矩陣的左上方的值。更具體而言,的卷積核是用來(lái)連接輸入矩陣中的9個(gè)值,并且將其轉(zhuǎn)變?yōu)檩敵鼍仃嚨囊粋€(gè)值的。一個(gè)卷積操作是一個(gè)多對(duì)一(many-to-one)的映射關(guān)系。讓我們記住這個(gè),我們接下來(lái)將會(huì)用得著。
反過(guò)來(lái)操作吧
現(xiàn)在,假設(shè)我們想要反過(guò)來(lái)操作。我們想要將輸入矩陣中的一個(gè)值映射到輸出矩陣的9個(gè)值,這將是一個(gè)一對(duì)多(one-to-many)的映射關(guān)系。這個(gè)就像是卷積操作的反操作,其核心觀點(diǎn)就是用轉(zhuǎn)置卷積。舉個(gè)例子,我們對(duì)一個(gè)的矩陣進(jìn)行上采樣為的矩陣。這個(gè)操作將會(huì)維護(hù)一個(gè)1對(duì)應(yīng)9的映射關(guān)系。
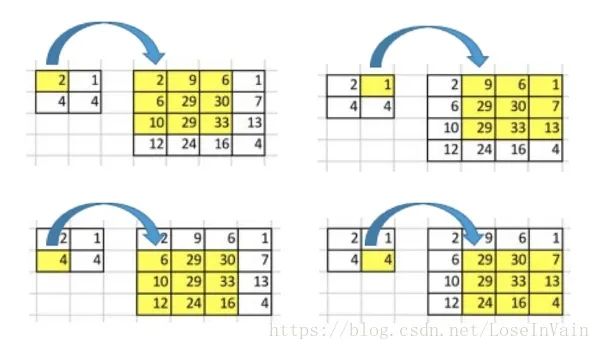
因此就結(jié)論而言,卷積操作是多對(duì)一,而轉(zhuǎn)置卷積操作是一對(duì)多,如下圖所示,每一個(gè)“對(duì)”而言,都需要維護(hù)一個(gè)權(quán)值。
但是我們將如何具體操作呢?為了接下來(lái)的討論,我們需要定義一個(gè)卷積矩陣(convolution matrix)和相應(yīng)的轉(zhuǎn)置卷積矩陣(transposed convolution matrix)。
卷積矩陣
我們可以將一個(gè)卷積操作用一個(gè)矩陣表示。這個(gè)表示很簡(jiǎn)單,無(wú)非就是將卷積核重新排列到我們可以用普通的矩陣乘法進(jìn)行矩陣卷積操作。如下圖就是原始的卷積核:

我們對(duì)這個(gè)的卷積核進(jìn)行重新排列,得到了下面這個(gè)的卷積矩陣:
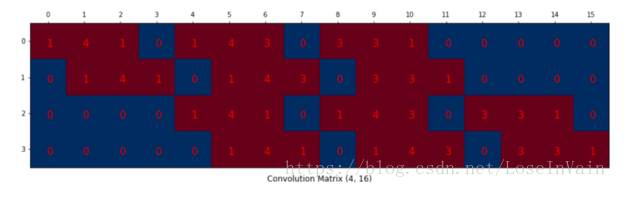
這個(gè)便是卷積矩陣了,這個(gè)矩陣的每一行都定義了一個(gè)卷積操作。下圖將會(huì)更加直觀地告訴你這個(gè)重排列是怎么進(jìn)行的。每一個(gè)卷積矩陣的行都是通過(guò)重新排列卷積核的元素,并且添加0補(bǔ)充(zero padding)進(jìn)行的。
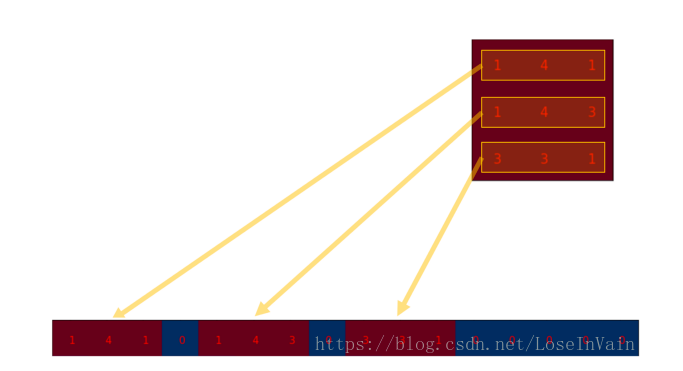
為了將卷積操作表示為卷積矩陣和輸入矩陣的向量乘法,我們將輸入矩陣攤平(flatten)為一個(gè)列向量,形狀為,如下圖所示。
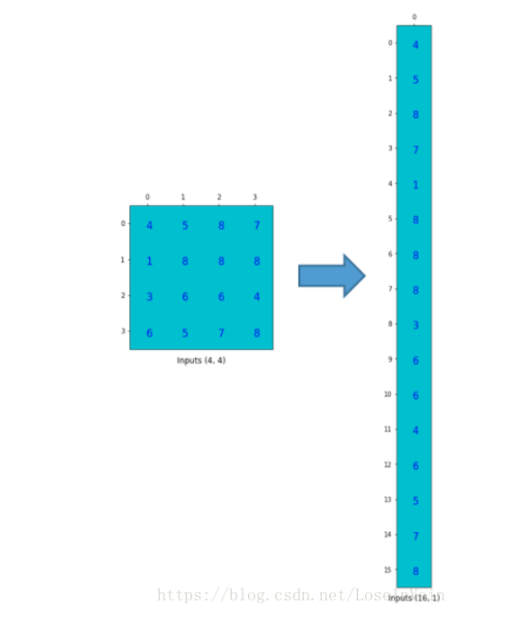
我們可以將這個(gè)的卷積矩陣和的輸入列向量進(jìn)行矩陣乘法,這樣我們就得到了輸出列向量。
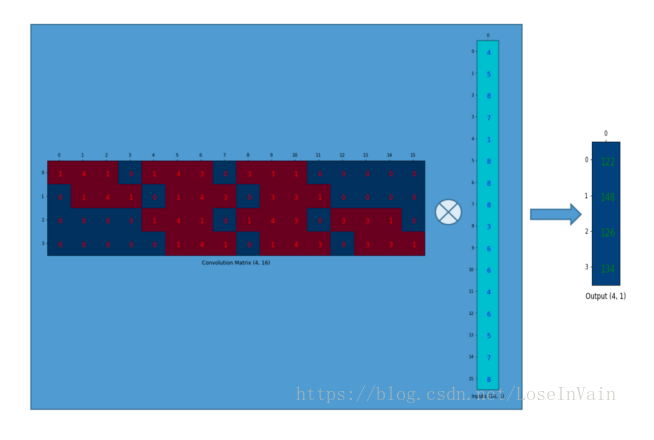
這個(gè)輸出的的矩陣可以重新塑性為一個(gè)的矩陣,而這個(gè)矩陣正是和我們一開(kāi)始通過(guò)傳統(tǒng)的卷積操作得到的一模一樣。

簡(jiǎn)單來(lái)說(shuō),這個(gè)卷積矩陣除了重新排列卷積核的權(quán)重之外就沒(méi)有啥了,然后卷積操作可以通過(guò)表示為卷積矩陣和輸入矩陣的列向量形式的矩陣乘積形式進(jìn)行表達(dá)。 所以各位發(fā)現(xiàn)了嗎,關(guān)鍵點(diǎn)就在于這個(gè)卷積矩陣,你可以從16()到4()因?yàn)檫@個(gè)卷積矩陣尺寸正是的,然后呢,如果你有一個(gè)的矩陣,你就可以從4()到16()了,這不就是一個(gè)上采樣的操作嗎?啊哈!讓我們繼續(xù)吧!
轉(zhuǎn)置卷積矩陣
我們想要從4()到16(),因此我們使用了一個(gè)的矩陣,但是還有一件事情需要注意,我們是想要維護(hù)一個(gè)1到9的映射關(guān)系。 假設(shè)我們轉(zhuǎn)置這個(gè)卷積矩陣變?yōu)椤N覀兛梢詫?duì)和列向量進(jìn)行矩陣乘法,從而生成一個(gè)的輸出矩陣。這個(gè)轉(zhuǎn)置矩陣正是將一個(gè)元素映射到了9個(gè)元素。
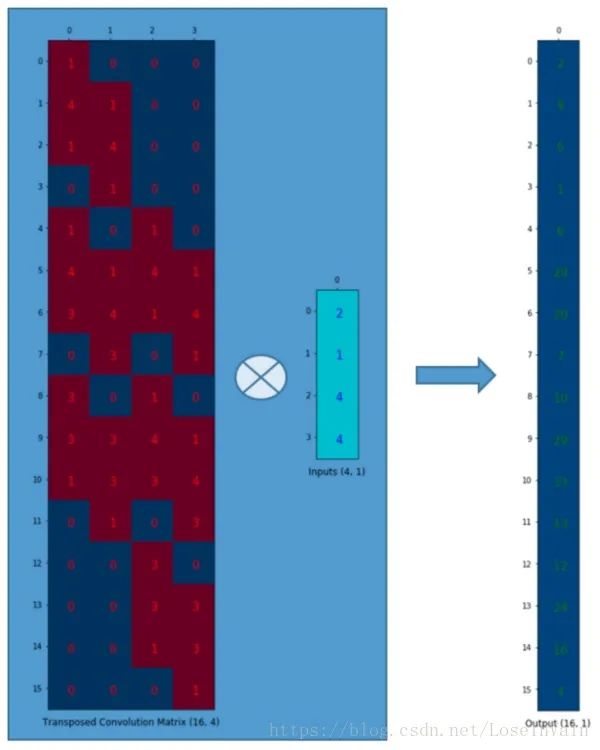
這個(gè)輸出可以塑形為的矩陣:

我們只是對(duì)小矩陣進(jìn)行上采樣為一個(gè)更大尺寸的矩陣。這個(gè)轉(zhuǎn)置卷積矩陣維護(hù)了一個(gè)1個(gè)元素到9個(gè)元素的映射關(guān)系,因?yàn)檫@個(gè)關(guān)系正表現(xiàn)在了其轉(zhuǎn)置卷積元素上。需要注意的是:這里的轉(zhuǎn)置卷積矩陣的參數(shù),不一定從原始的卷積矩陣中簡(jiǎn)單轉(zhuǎn)置得到的,轉(zhuǎn)置這個(gè)操作只是提供了轉(zhuǎn)置卷積矩陣的形狀而已。
總結(jié)
轉(zhuǎn)置卷積操作構(gòu)建了和普通的卷積操作一樣的連接關(guān)系,只不過(guò)這個(gè)是從反向方向開(kāi)始連接的。我們可以用它進(jìn)行上采樣。另外,這個(gè)轉(zhuǎn)置卷積矩陣的參數(shù)是可以學(xué)習(xí)的,因此我們不需要一些人為預(yù)先定義的方法。即使它被稱(chēng)為轉(zhuǎn)置卷積,它并不是意味著我們將一些現(xiàn)存的卷積矩陣簡(jiǎn)單轉(zhuǎn)置并且使用其轉(zhuǎn)置后的值。 從本質(zhì)來(lái)說(shuō),轉(zhuǎn)置卷積不是一個(gè)卷積,但是我們可以將其看成卷積,并且當(dāng)成卷積這樣去用。我們通過(guò)在輸入矩陣中的元素之間插入0進(jìn)行補(bǔ)充,從而實(shí)現(xiàn)尺寸上采樣,然后通過(guò)普通的卷積操作就可以產(chǎn)生和轉(zhuǎn)置卷積相同的效果了。你在一些文章中將會(huì)發(fā)現(xiàn)他們都是這樣解釋轉(zhuǎn)置卷積的,但是這個(gè)因?yàn)樵诰矸e操作之前需要通過(guò)添加0進(jìn)行上采樣,因此是比較低效率的。注意:轉(zhuǎn)置卷積會(huì)導(dǎo)致生成圖像中出現(xiàn)棋盤(pán)效應(yīng)(checkerboard artifacts),這篇文章《Deconvolution and Checkerboard Artifacts》推薦了一種上采樣的操作(也就是插值操作),這個(gè)操作接在一個(gè)卷積操作后面以減少這種現(xiàn)象。如果你的主要目的是生成盡可能少棋盤(pán)效應(yīng)的圖像,那么這篇文章就值得你去閱讀。
-
卷積
+關(guān)注
關(guān)注
0文章
95瀏覽量
18548
原文標(biāo)題:一文搞懂轉(zhuǎn)置卷積(反卷積)
文章出處:【微信號(hào):tyutcsplab,微信公眾號(hào):智能感知與物聯(lián)網(wǎng)技術(shù)研究所】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
使用PyTorch深度解析卷積神經(jīng)網(wǎng)絡(luò)
卷積神經(jīng)網(wǎng)絡(luò)—深度卷積網(wǎng)絡(luò):實(shí)例探究及學(xué)習(xí)總結(jié)
解析深度學(xué)習(xí):卷積神經(jīng)網(wǎng)絡(luò)原理與視覺(jué)實(shí)踐
C語(yǔ)言教程之矩陣的轉(zhuǎn)置
如何使用基于轉(zhuǎn)置卷積操作改進(jìn)進(jìn)行單階段多邊框目標(biāo)檢測(cè)方法
深度學(xué)習(xí)中的各種卷積網(wǎng)絡(luò)大家知多少
探析深度學(xué)習(xí)中的各種卷積

一篇文章搞定CNN轉(zhuǎn)置卷積
深度學(xué)習(xí)&計(jì)算機(jī)視覺(jué)方向的相關(guān)面試題
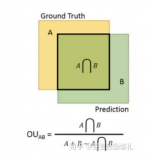
深入理解深度學(xué)習(xí)中的反(轉(zhuǎn)置)卷積

PyTorch教程14.10之轉(zhuǎn)置卷積

深度學(xué)習(xí)中的各種卷積原理解析
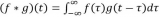
MATLAB | 這是我見(jiàn)過(guò)最離譜的轉(zhuǎn)置操作





 深度解析什么是轉(zhuǎn)置卷積
深度解析什么是轉(zhuǎn)置卷積










評(píng)論