我們已經講述了PID控制器的實現，包括位置型PID控制器和增量型PID控制器。但這個實現只是最基本的實現，并沒有考慮任何的干擾情況。在本節及后續的一些章節，我們就來討論一下經典PID控制器的優化與改進。這一節我們首先來討論針對積分項的積分分離優化算法。

1、基本思想

我們已經講述了PID控制引入積分主要是為了消除靜差，提高控制精度。但在過程的啟動、結束或大幅度增減設定值時，短時間內系統輸出有很大偏差，會造成PID運算的積分累積，引起超調或者振蕩。為了解決這一干擾，人們引入了積分分離的思想。其思路是偏差值較大時，取消積分作用，以免于超調量增大；而偏差值較小時，引入積分作用，以便消除靜差，提高控制精度。

具體的實現步驟是：根據實際情況，設定一個閾值；當偏差大于閾值時，消除積分僅用PD控制；當偏差小于等于閾值時，引入積分采用PID控制。則控制算法可表示為：

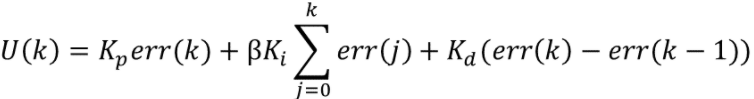
其中β稱為積分開關系數，其取值范圍為：

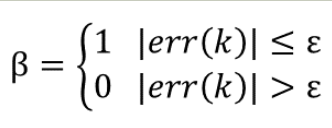
由上述表述及公式我們可以知道，積分分離算法的效果其實與ε值的選取有莫大關系，所以ε值的選取實際上是實現的難點，ε值過大則達不到積分分離的效果，而ε值過小則難以進入積分區，ε值的選取存在很大的主觀因素。

對于經典的增量式PID算法，似乎沒有辦法由以上的公式推導而來，因為β隨著err(k)的變化在不是修改著控制器的表達式。其實我們可以換一種角度考慮，每次系統調節未定后，偏差應該為零，然后只有當設定值改變時，系統才會響應而開始調節。設定值的改變實際上是一個階躍變化，此時的控制輸出記為U0，開始調節時，其調節增量其實與之前的一切沒有關系。所以我們就可以以變化時刻開始為起點，而得到帶積分分離的增量算法，以保證在啟動、停止和快速變化時防止超調。公式如下：

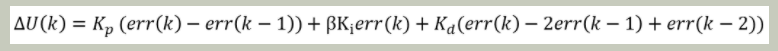
其中β的取值與位置型PID算法一致。可能有人會擔心偏差來回變化，造成積分作用的頻繁分離和引入，進而使上述的增量表達式無法實現。其實我們分析一下就能發現，在開始時，由于設定值變化引起的偏差大而分離了積分作用，在接近設定值時，偏差變小就引入了積分，一邊消除靜差，而后處于穩態，直到下一次變化。

2、算法實現

這一部分，我們根據前面對其基本思想的描述，來實現基于積分分離的PID算法實現，同樣是包括位置型和增量型兩種實現方式。首先我們來看一下算法的實現過程，具體的流程圖如下：

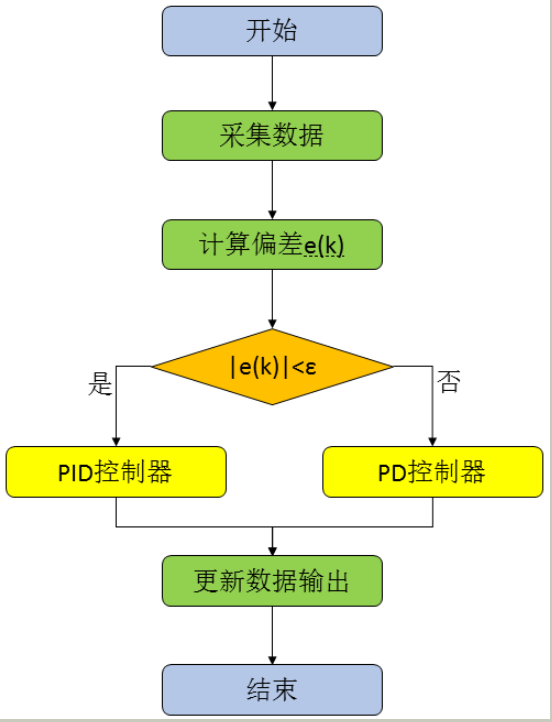
有上圖我們知道，與普通的PID算法的區別，只是判斷偏差的大小，偏差大時，為PD算法，偏差小時為PID算法。于是我們需要一個偏差檢測與積分項分離系數β的函數。

 1 static uint16_t BetaGeneration(float error,float epsilon)
 2 
 3 {
 4 
 5   uint16_t beta=0;
 6 
 7   if(abs(error)<= epsilon)
 8 
 9 {
10 
11   beta=1;
12 
13 }
14 
15 return beta;
16 
17 }

（1）位置型PID算法實現

根據前面的分析我們可以很輕松的編寫程序，只需要在編寫程序時判斷偏差以確定是否引入積分項就可以了。同樣先定義PID對象的結構體：

 1 /*定義結構體和公用體*/
 2 
 3 typedef struct
 4 
 5 {
 6 
 7   float setpoint;       //設定值
 8 
 9   float proportiongain;     //比例系數
10 
11   float integralgain;      //積分系數
12 
13   float derivativegain;    //微分系數
14 
15   float lasterror;     //前一拍偏差
16 
17   float result; //輸出值
18 
19   float integral;//積分值
20 
21   float epsilon; //偏差檢測閾值
22 
23 }PID;

接下來實現PID控制器：

 1 void PIDRegulation(PID *vPID, float processValue)
 2 
 3 {
 4 
 5   float thisError;
 6 
 7   thisError=vPID->setpoint-processValue;
 8 
 9   vPID->integral+=thisError;
10 
11   uint16_t beta= BetaGeneration(error, vPID->epsilon);
12 
13   if(beta>0)
14 
15 {
16 
17   vPID->result=vPID->proportiongain*thisError+vPID->derivativegain*(thisError-vPID->lasterror);
18 
19 }
20 
21 else
22 
23 {
24 
25 vPID->result=vPID->proportiongain*thisError+vPID->integralgain*vPID->integral+vPID->derivativegain*(thisError-vPID->lasterror);
26 
27 }
28 
29  
30 
31   vPID->lasterror=thisError;
32 
33 }

與普通的PID算法的區別就是上述代碼中增加了偏差判斷，來決定積分項的分離與否。

（2）增量型PID算法實現

對于增量型PID控制，我們也可以采取相同的處理。首先定義PID對象的結構體：

 1 /*定義結構體和公用體*/
 2 
 3 typedef struct
 4 
 5 {
 6 
 7   float setpoint;       //設定值
 8 
 9   float proportiongain;     //比例系數
10 
11   float integralgain;      //積分系數
12 
13   float derivativegain;    //微分系數
14 
15   float lasterror;     //前一拍偏差
16 
17   float preerror;     //前兩拍偏差
18 
19   float deadband;     //死區
20 
21   float result; //輸出值
22 
23   float epsilon; //偏差檢測閾值
24 
25 }PID;

接下來實現PID控制器：

 1 void PIDRegulation(PID *vPID, float processValue)
 2 
 3 {
 4 
 5   float thisError;
 6 
 7   float increment;
 8 
 9   float pError,dError,iError;
10 
11  
12 
13   thisError=vPID->setpoint-processValue; //得到偏差值
14 
15   pError=thisError-vPID->lasterror;
16 
17   iError=thisError;
18 
19   dError=thisError-2*(vPID->lasterror)+vPID->preerror;
20 
21   uint16_t beta= BetaGeneration(error, vPID->epsilon);
22 
23   if(beta>0)
24 
25 {
26 
27 increment=vPID->proportiongain*pError+vPID->derivativegain*dError;   //增量計算
28 
29 }
30 
31 else
32 
33 {
34 
35 increment=vPID->proportiongain*pError+vPID->integralgain*iError+vPID->derivativegain*dError;   //增量計算
36 
37 }
38 
39   vPID->preerror=vPID->lasterror;  //存放偏差用于下次運算
40 
41   vPID->lasterror=thisError;
42 
43   vPID->result+=increment;
44 
45 }

這就實現了增量型PID控制器積分分離算法，也沒有考慮任何的干擾條件，僅僅只是對數學公式的計算機語言化。

3、總結

積分分離算法的思想非常簡單。當然，對于β的取值，很多人提出了改進措施，例如分多段取值，設定多個閾值ε1、ε2、ε3、ε4等，不過這些閾值也需要根據實際的系統來設定。除了分段取值外，甚至也有采用函數關系來獲取β值。當然，這樣處理后就不再是簡單的積分分離了，特別是在增量型算法中，實際上已經演變為一種變積分算法了。已經偏離了積分分離算法的設計思想，在后面我們會進一步說明。
編輯：hfy