從卡諾定理如何到熵增加原理？這篇文章為你來捋一捋思路。

1824年，法國科學家卡諾提出：工作在兩個恒溫熱源之間的一切熱機，以可逆熱機的效率為最高。此即卡諾定理。

在歷史上，卡諾定理曾是熱力學第二定律的基礎，但現在，它可從熱力學第二定律推得，具體方法是采用反證法，下面先來講一講這個證明過程。

01

證明卡諾定理

現考慮兩個熱機M和M'，其中M為可逆熱機，而M'為一般熱機，即M'有可能是可逆熱機，也有可能是不可逆熱機。

兩臺熱機都工作在兩個熱源和之間，設。假設它們從高溫熱源吸熱分別為和，且。向低溫熱源放熱分別為和，做功分別為和，效率分別為和。

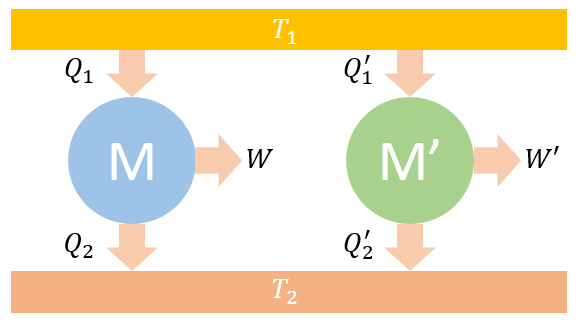
用反證法，設，則由于，故，既然M是可逆的，則可將的一部分拿來推動M逆向工作，即讓M成為一個制冷機。所以M現在從低溫熱源吸熱，向高溫熱源放熱。

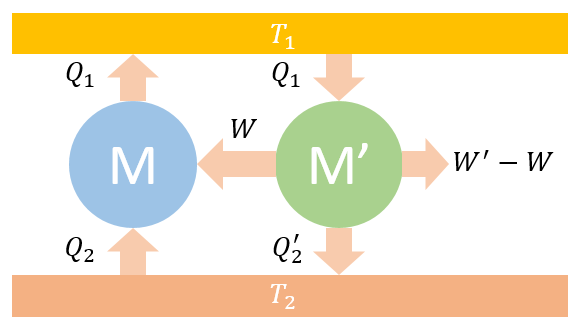
把這兩個熱機聯合成一個總熱機M''，該總熱機與沒有熱交換，只與發生熱交換，其值為，同時總熱機對外做功為。

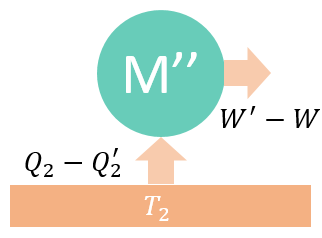
顯然，這等于實現了“從單一熱源吸熱并做功而不產生其他影響”的美夢，違反了熱力學第二定律的開爾文表述。這說明前面的假設是錯誤的，正確的結果只能是如果M為一般熱機，而M'為可逆熱機，那么也會得到所以，當M和M'都為可逆熱機時，上面兩式同時成立，那只能是所以，工作在兩個恒溫熱源之間的一切可逆熱機的效率相等，工作在兩個恒溫熱源之間的任何熱機的效率不可能比可逆熱機的高。

這就證明了卡諾定理了。它看起來就像一條數學定理，的確，要不然怎么叫定理呢？物理中的定理是一種可以證明的命題。這一點與物理定律不同，物理定律是從實驗中歸納總結出來的，無法也無須證明。

02

澄清一個誤解

值得注意的是，卡諾定理強調了一點：工作在兩個恒溫熱源之間的熱機！

這意味著什么呢？

這意味著，你的熱機只能與兩個恒溫熱源發生熱交換，除此之外的過程，系統不能再吸放熱，這正好就是卡諾循環的要求嘛！

所謂卡諾循環是指，工作物質只與兩個恒溫熱源交換熱量，除此之外，不再存在任何吸放熱的過程。

所以，工作在兩個恒溫熱源之間的循環就是卡諾循環！工作在兩個恒溫熱源之間的熱機就是卡諾熱機。

因此，卡諾定理中提到的熱機必然是卡諾熱機，只是分為可逆或不可逆罷了。

溫馨提示：很多人認為卡諾循環一定是可逆的，這是一種誤解，卡諾循環只是規定工作物質工作在兩個恒溫熱源之間，并沒有說過程一定可逆！

如果卡洛循環還是可逆的，且工作物質是理想氣體，由于熱機交換熱的時候經歷的是等溫變化，所以必然對應兩條等溫線。而理想氣體的等溫線不會相交，要構成循環，必須還要另外兩條線來幫忙！而另一方面，既然已經要求該熱機不能與別的熱源交換熱，這另外的兩條線必然都是絕熱線。所形成的循環就是理想氣體的準靜態的卡諾循環，也就是可逆的卡諾循環，其P-V圖如下所示。

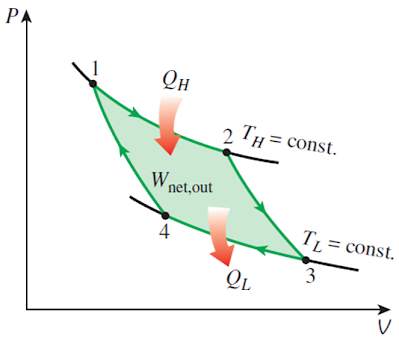
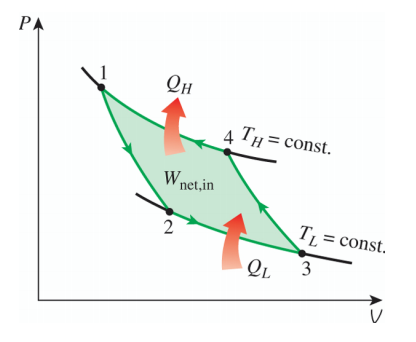
如果卡諾循環不是可逆的，那循環過程不是準靜態的，也就沒法用曲線來表示了，只能通過一個熱機模型圖來表示，如下圖所示。

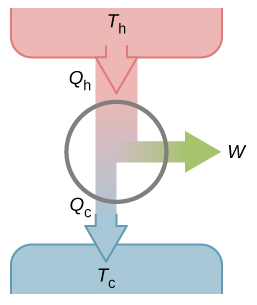
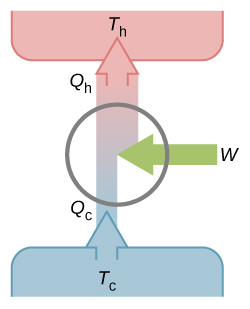
至于有人說：可逆的卡諾熱機的效率最高。

這是不對的！

因為，對于工作在非卡諾循環上的熱機來說，其效率不一定比可逆卡諾熱機小。其實，非卡諾熱機的效率要另當別論，因為它們與卡諾定理沒有關系。

當然，一切熱機的效率肯定不會達到1，這是熱力學第二定律決定的。

03

理想氣體的卡諾循環

要注意，前面提到的卡諾循環是普遍的，并沒有限制工作物質的種類，所以卡諾定理對任意工作物質都成立。換句話說，無論熱機的工作物質是什么，只要是工作在兩個確定溫度的熱源之間的可逆熱機，其效率都一樣！

因此，當根據一種特殊而熟悉的工作物質——理想氣體來具體分析時，得到的可逆卡諾循環的效率應該就代表了任何可逆卡諾熱機效率！

考慮一定質量的理想氣體，設它經歷一個順時針的準靜態卡諾循環，也就是沿著由兩條等溫線和兩條絕熱線圍成的回路。

這個過程比較繁瑣，但大多數熱學書上都有，這里就直接給出結果吧。

經過計算得，理想氣體的可逆卡諾循環的效率為其中是高溫熱源的溫度，是低溫熱源的溫度。這就是工作在高溫和低溫之間的一切可逆卡諾熱機的效率。

既然得到了可逆卡諾熱機效率的值，那么卡諾定理現在可表述為左邊代表一般卡諾熱機的效率，右邊代表可逆的卡諾熱機的效率。

04

克勞修斯不等式

根據卡諾定理可知即由于實際上是代表放熱，如果約定放熱用負數表示，那么上式應該改為因此得到我們將每一項叫做熱溫比。由此可見，卡諾循環的熱溫比之和小于或等于零，等號在循環可逆時成立。此式是任何卡諾循環都滿足的要求。

由于這兩個溫度一高一低，分別吸熱和放熱，如果用表示高溫，用表示低溫，用表示放熱，用表示吸熱，則上式可以寫成對任意一個循環過程，如下圖中的循環ABCDA，我們總可以將其分割成無數個卡諾循環，那么，整個循環相當于這些卡諾循環的總和。

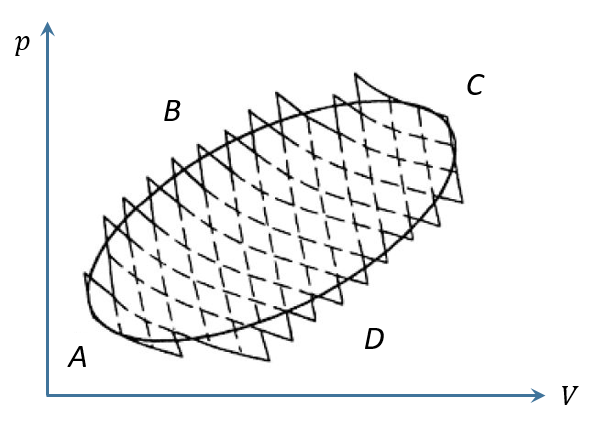
每個卡諾循環對應兩個溫度，相鄰的卡諾循環會共用一個溫度，從左至右，這些溫度依次是，，，，。

注意，這里的一般應為無窮大，否則不能確保一個任意的循環能被分割成卡諾循環。

由于每個卡諾循環有一個高溫和一個低溫，都滿足上面的不等式，若將所有卡諾循環的不等式加起來，就是

由于每相鄰的兩個卡諾循環都共用一條等溫線，這條等溫線在兩個卡諾循環中的貢獻會合成一項。例如，對第條等溫線來說，它在前一個循環上吸熱，在后一個循環上放熱，二者抵消后得到的總熱值就是這條等溫線上的熱交換量，記作

由于第1條和第條等溫線都沒有被兩個卡諾循環共有，所以因此，這第條等溫線對應的項為，也就是一個熱溫比。既然每條等溫線都對應一個熱溫比，把所有這些熱溫比都加起就是

若上述分割的每個卡諾循環無限小，則上式就變成連續的求和，也就是積分，即

這就是大名鼎鼎的克勞修斯不等式。

05

熱力學熵的定義

對克勞修斯不等式來說，當循環過程可逆時，等號成立；當循環過程不可逆時，小于號成立。

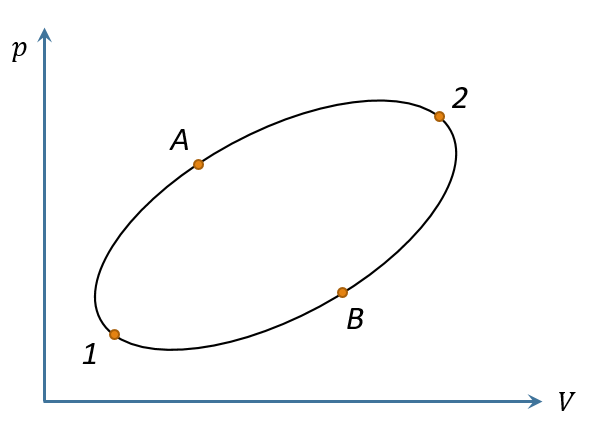
對上圖所示循環過程1→A→2→B→1，則有

將其分成過程1→A→2和2→B→1，則即這說明熱溫比的積分與路徑無關，或者說，它的積分只取決于始末兩點，因此必定存在一個由狀態決定的函數，它在始末兩點的取值之差剛好等于的沿任意可逆路徑的積分，即可逆

關于“為什么必定存在一個由狀態決定的函數”這一點，可與保守力做功類比，勢能函數也是類似得到的。具體可參看文章《什么是保守力？》的第4節的有關推導。

這個狀態函數就是克勞修斯熵，也叫熱力學熵。上式即為熱力學熵的定義式。對一個微小的過程來說，熵的微分就是熱溫比，即

注意，熱力學熵的定義并沒有給出熵的絕對值，只給出了熵在不同狀態的改變量，這個改變量是通過計算熱溫比在連接兩個態的可逆路徑上的積分來獲得。

雖然熵的值本來只與狀態有關，但現在沒法知道它到底如何由狀態決定，所以只能通過計算熱溫比的積分來獲得它在不同態之間的差值。

根據熱力學第一定律，再結合熵的微分關系可知此式將熱力學第一、第二定律結合起來了，避免了非狀態量，是最一般的熱力學關系，稱之為熱力學基本方程。根據此方程，可以通過構造合適的可逆過程來計算不同態之間的熵差。

06

熵增加原理

再次回到克勞修斯不等式上面通過分析等號的情形引入了熵的定義，那么如果考慮一個一般的循環會有什么結果呢？

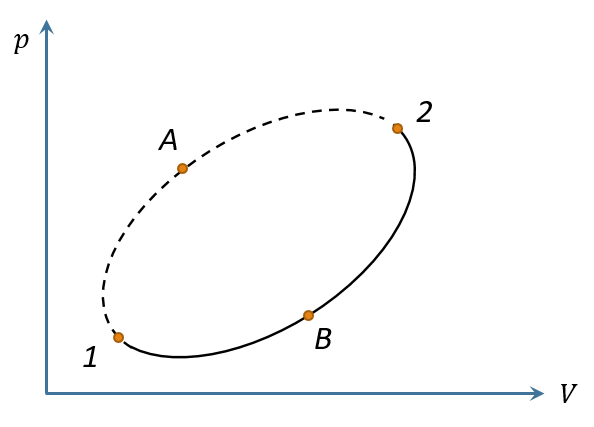
考慮一個循環1→A→2→B→1，設2→B→1是可逆過程，但1→A→2是一般過程，即可能可逆也可能不可逆。根據克勞修斯不等式有則也就是而既然2→B→1是可逆過程，根據熵的定義，有故得令，考慮到1→A→2是一般過程，直接記為1→2即可，因此上式可寫為此式告訴我們，任意過程中的熱溫比的積累不會比它連接的兩個態的熵差大。

對絕熱過程，顯然右邊為零，因此這說明，絕熱過程的不會減少。而孤立系統經歷的過程當然是絕熱的，因此孤立系統的熵永不減少，這就是熵增加原理。

根據熵增加原理，對孤立系統而言，除非經歷可逆過程，否則熵就會增大！由于實際中可逆過程很難實現，所以熵增加原理告訴我們：實際中的孤立的系統熵一般都是增加的。

07

循環和非循環過程的熵變

熱力學過程可能是循環，可能是有始有終的過程，下面分別看看它們對應的熵變。

先來看循環過程。

既然循環是指回到了初態，初末態相同，而熵是態函數，只跟位置有關，因此循環過程無論可逆與否，均有。所以，循環過程不存在考慮熵變的問題！

不過需要注意的是，循環沒有熵變不是指任何兩點之間沒有熵變，而是指一個完整的的循環不會導致熵變，且沒有考慮外界的情況。

另外，根據克勞修斯不等式若為可逆循環，上式取等號，而若為不可逆循環，則取小于號。

再來看非循環的過程。

根據上節的結論，對任意過程，熵增不會比熱溫比的積累小，即

當過程可逆時且不絕熱時，則有

注意，此時熱溫比的積累可正可負，取決于是放熱還是吸熱，若是放熱，熵減少，反之則熵增加。

當過程可逆又絕熱時，則有

當過程不可逆且不絕熱時，則有

注意，此時熱溫比的積累可正可負，取決于是放熱還是吸熱，若是放熱，熵可能減少也可能增加，若是吸熱，則熵必然增加。

當過程不可逆且絕熱時，則有這就是最常見的孤立系統的情形，熵增加原理也是因之而得其名。

審核編輯 ：李倩