前面我們基本把有感FOC介紹得差不多了，接下來我本打算進入無感FOC控制的深入學習，奈何導師項目項目太多太雜........................先把自己這段時間學的東西總結分享一下再說吧。查閱了很多無感FOC控制的相關資料，把基本原理和流程漸漸的了解了一下（以后有時間再詳細介紹了），發現很多環節都會用到”一階低通數字濾波器“（相電流濾波，反電勢濾波，角度、轉速濾波，校正因子濾波），雖然代碼里面只是一個簡單的公式，但為了控制系統的參數設計，我還是淺淺的去探究了一下其基本原理，如有錯誤還望提出指正。

開局先直接給出公式：

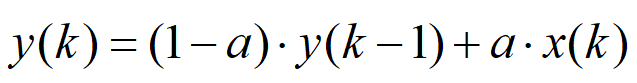
式中：x(k)為當前輸入，y(k-1)為上一次的輸出，y(k)為當前計算的輸出；a為濾波系數，取值范圍0~1，a取值越小，當前輸入權重就越小，輸出波形越平滑，但響應靈敏度降低；

如果只是套用公式寫代碼的話，看到這里就可以結束了，想要理解其中的原理，以及采樣頻率、截止頻率和參數的計算，那么請接著往下看。

01. 原理及公式推導

”一階低通數字濾波器“對應的物理電路模型是”一階RC低通濾波電路“，電路如下圖所示。

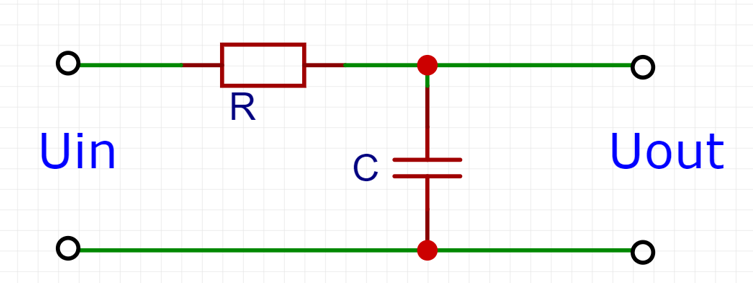
電容的阻抗表示為1/jωC，對于上面電路，有輸入輸出電壓關系：

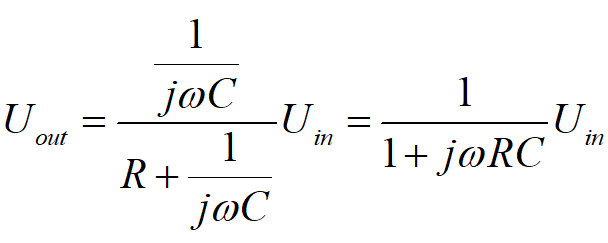
上式寫成傳遞函數形式：

，

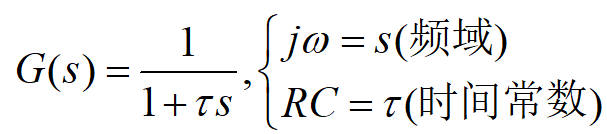在《自動控制原理》中稱為一階慣性環節。

由Y(s)=G(s).F(s)得到時域的微分方程：

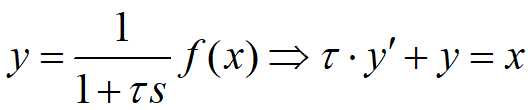
使用一階后向差分法，對上面微分方程進行離散化，有：

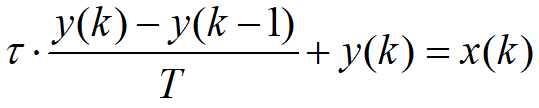
其中T為采樣周期，對上式進行整理化簡可寫成：

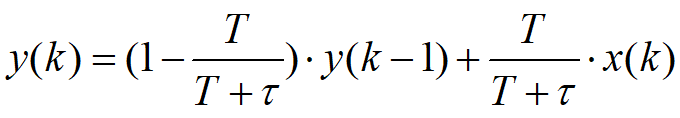
令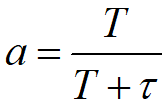得到一般表達式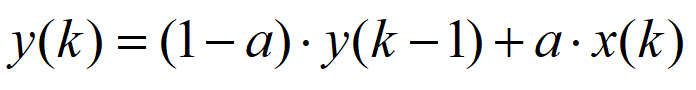：，a稱為濾波系數。

02. 截止頻率和參數計算

對于電路模型，有截止頻率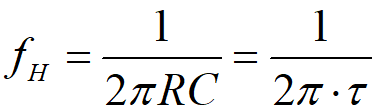（截止頻率定義為幅頻響應曲線衰減 -3db，即為原來的1/sqrt(2)時的頻率，模電里面的基礎知識這里不細講）

可得是將常數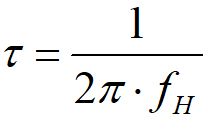

代入濾波系數a的表達式得：

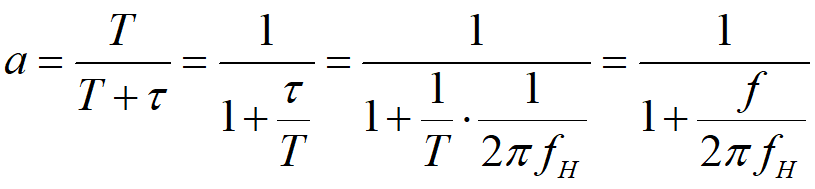
式中f=1/T為采樣頻率。

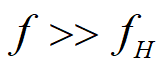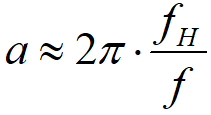在實際的應用中，一般有采樣頻率遠大于截止頻率，即有，故近似有，所以已知截止頻率和采樣頻率，我么就能夠計算濾波系數a的值了。

又會問：截止頻率和采樣頻率怎么確定呢？選取不同的值會對計算輸出有什么影響呢？下面為你簡單介紹一下。

03. 頻率的選擇

3.1采樣頻率的選擇

一般人為主觀選擇，在不影響其他功能性能的條件下，盡量越大越好。

先以我之前做的電機控制為例。在程序中，PWM定時器開啟中斷，在中斷服務函數中用ADC采集相電流，故采樣頻率就等于PWM定時器頻率，我在控制代碼中用的是20kHz，即采樣頻率f=20kHz。

3.2截止頻率的選擇

根據采樣對象信號的頻率選擇，一般稍大于被采樣信號的最大基波頻率就好。

還是以我做的電機控制為例。我用的永磁同步電機額定轉速為3000rpm，極對數為4，采樣對象為相電流。則在額定條件下，相電流的頻率為f_current=3000*4/60=200Hz，考慮到電機超負荷運行，瞬時轉速可以大于3000，保留一定余量，我取截止頻率f_H=500Hz。如此計算得濾波系數。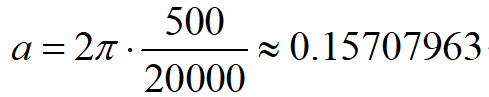

在電機運行前，對放大器進行校準時，只考慮直流偏置輸入，即被采樣的信號頻率趨近于0Hz，主要濾掉電路中的高頻干擾和噪聲，故可把截止頻率取得很小，我這里取f_H=5Hz，計算得濾波系數a=0.00157。

04頻率選擇對輸出的影響（附仿真分析）

在采樣頻率固定的情況下，截止頻率越大，濾波系數a的值越大，當前輸入的權重就越大，計算的輸出和實際的輸出跟蹤效果更好，即動態響應更好，幅值衰減的影響更小。

減小截止頻率，濾波系數a的值越小，當前輸入的權重越小，故計算的輸出信號更平滑，對噪聲干擾和諧波的濾除效果更好，但是動態響應變差，而且會產生一定程度的幅值衰減。

下面是matlab代碼和仿真結果分析：

仿真結果：

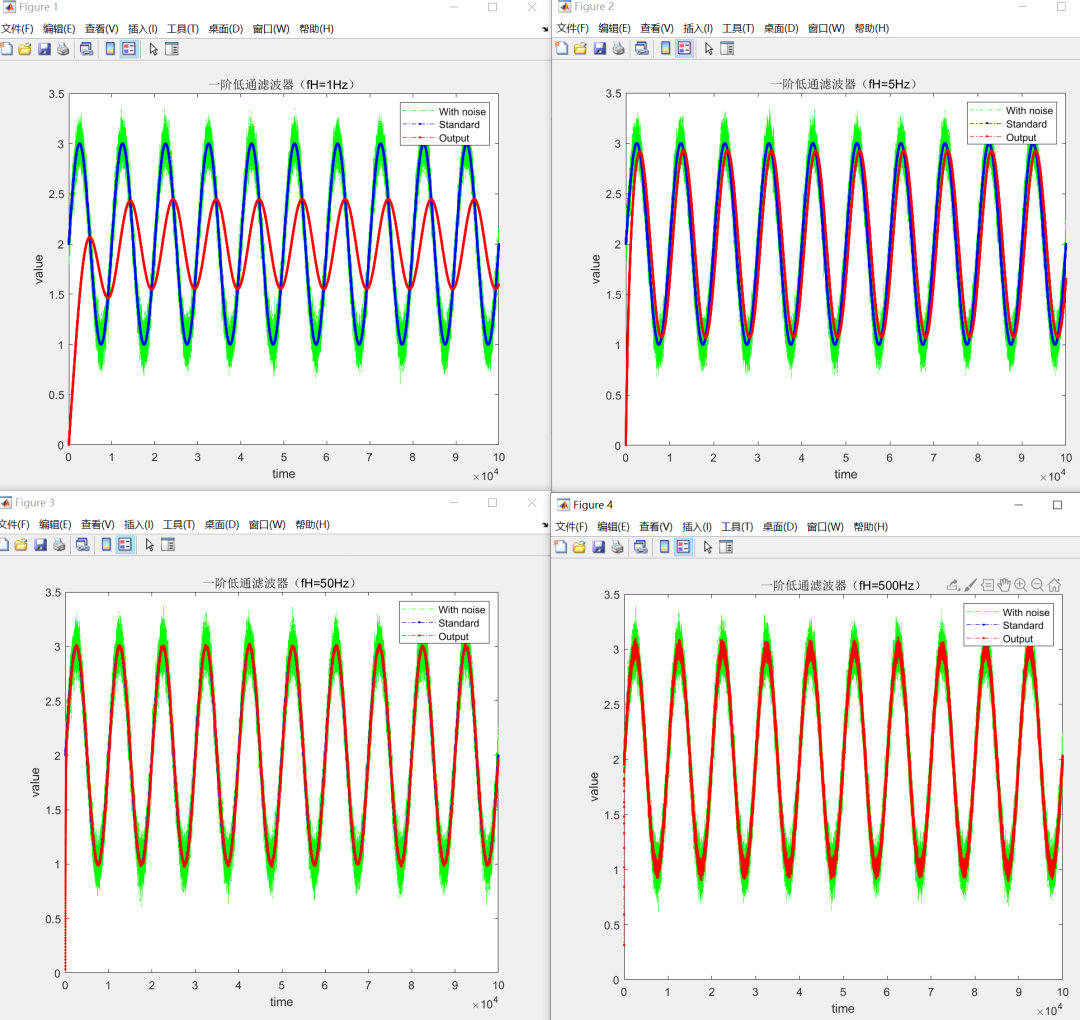
圖中，綠色為含有噪聲的采樣信號，藍色為標準的正弦信號，紅色為采樣信號經過一階低通濾波器的計算輸出。

可以發現，當截止頻率較小時，輸出信號幅值衰減明顯，且存在一定滯后；隨著截止頻率的增大，對標準正弦信號的跟蹤效果越好；當截止頻率過大時，幾乎能完全復現采樣信號，但是對噪聲的濾波效果變差。

下面再看一下對直流信號的測試

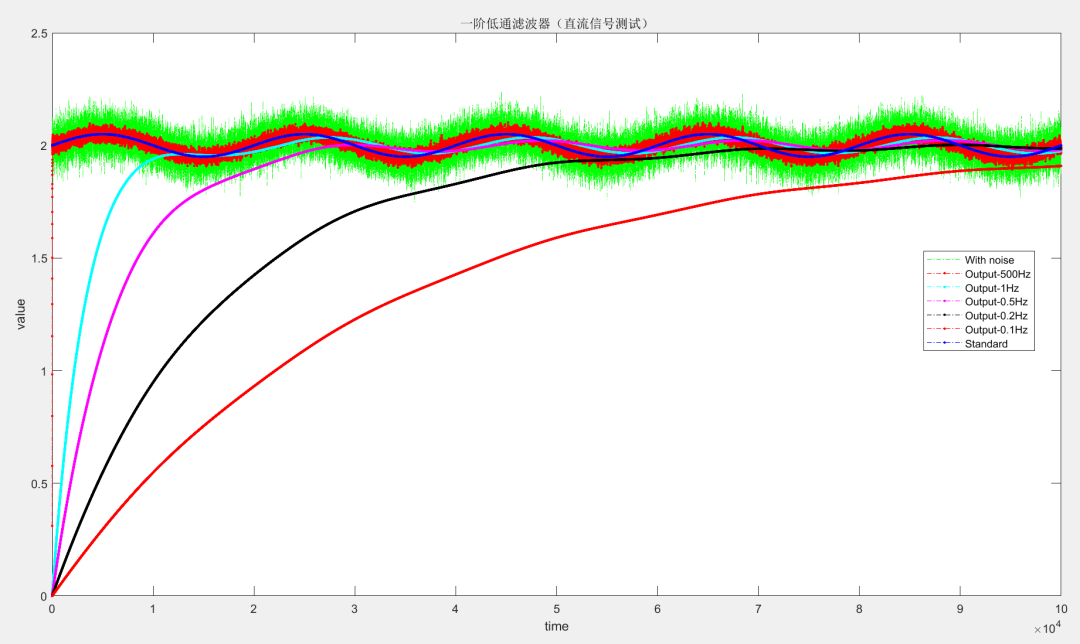
可以看出，隨著截止頻率的減小，計算輸出的信號越來越平滑，接近直流信號，但同時調節時間也增大，對應我前面電機控制中，對放大器的校準時間需要延長。在實際應用中，對于直流信號的濾波，截止頻率一般取1~50Hz我覺得就好了（當然也有可能其它情況我沒想到）。

最后附上matlab的仿真源代碼

代碼源程序：

交流信號部分：

f_basic=200;%原信號頻率為200Hzw_basic=2*pi*f_basic;f_H=1;%截止頻率500Hzf_simple=20000;%采樣頻率20kHzPointNumber = 100000;%坐標點數量
x=0PointNumber-1;Standard =2+sin(w_basic*x*0.0000005);%原始標準信號noise = 0+0.1*randn(1,PointNumber);AddNoise=Standard+noise;
a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endfigure(1);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,Standard,'-..b');hold on;plot(X,output,'-..r');hold on;legend('With noise','Standard','Output') xlabel('time');ylabel('value');title('一階低通濾波器（fH=1Hz）');


f_basic=200;%原信號頻率為200Hzw_basic=2*pi*f_basic;f_H=5;%截止頻率500Hzf_simple=20000;%采樣頻率20kHzPointNumber = 100000;%坐標點數量
x=0PointNumber-1;Standard =2+sin(w_basic*x*0.0000005);%原始標準信號noise = 0+0.1*randn(1,PointNumber);AddNoise=Standard+noise;
a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endfigure(2);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,Standard,'-..b');hold on;plot(X,output,'-..r');hold on;legend('With noise','Standard','Output') xlabel('time');ylabel('value');title('一階低通濾波器（fH=5Hz）');

f_basic=200;%原信號頻率為200Hzw_basic=2*pi*f_basic;f_H=50;%截止頻率500Hzf_simple=20000;%采樣頻率20kHzPointNumber = 100000;%坐標點數量
x=0PointNumber-1;Standard =2+sin(w_basic*x*0.0000005);%原始標準信號noise = 0+0.1*randn(1,PointNumber);AddNoise=Standard+noise;


a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endfigure(3);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,Standard,'-..b');hold on;plot(X,output,'-..r');hold on;legend('With noise','Standard','Output') xlabel('time');ylabel('value');title('一階低通濾波器（fH=50Hz）');

f_basic=200;%原信號頻率為200Hzw_basic=2*pi*f_basic;f_H=500;%截止頻率500Hzf_simple=20000;%采樣頻率20kHzPointNumber = 100000;%坐標點數量
x=0PointNumber-1;Standard =2+sin(w_basic*x*0.0000005);%原始標準信號noise = 0+0.1*randn(1,PointNumber);AddNoise=Standard+noise;


a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endfigure(4);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,Standard,'-..b');hold on;plot(X,output,'-..r');hold on;legend('With noise','Standard','Output') xlabel('time');ylabel('value');title('一階低通濾波器（fH=500Hz）');

直流信號部分：

f_basic=1;%原信號頻率為200Hzw_basic=2*pi*f_basic;f_H=500;%截止頻率500Hzf_simple=20000;%采樣頻率20kHzPointNumber = 100000;%坐標點數量
x=0PointNumber-1;Standard =2+0.05*sin(w_basic*x*0.00005);%原始標準信號noise = 0+0.05*randn(1,PointNumber);AddNoise=Standard+noise;
a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endfigure(1);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,output,'-..r');hold on;
xlabel('time');ylabel('value');title('一階低通濾波器（直流信號測試）');
f_H=1;%截止頻率500Hza=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endplot(X,output,'-..c');hold on;
f_H=0.5;%截止頻率500Hza=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endplot(X,output,'-..m');hold on;
f_H=0.2;%截止頻率500Hza=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endplot(X,output,'-..k');hold on;


f_H=0.1;%截止頻率500Hza=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1    x_now=AddNoise(i+1);    y_now=(1-a)*y_last+a*x_now;    output(i+1)=y_now;    y_last=y_now;endplot(X,output,'-..r');hold on;
plot(X,Standard,'-..b');hold on;
 legend('With noise','Output-500Hz','Output-1Hz','Output-0.5Hz','Output-0.2Hz','Output-0.1Hz','Standard')