簡介

隨著深度學習的發展和普及，很多非結構數據被表示為高維向量，并通過近鄰搜索來查找，實現了多種場景的檢索需求，如人臉識別、圖片搜索、商品的推薦搜索等。另一方面隨著互聯網技術的發展及5G技術的普及，產生的數據呈爆發式增長，如何在海量數據中精準高效的完成搜索成為一個研究熱點，各路前輩專家提出了不同的算法，今天我們就簡單聊下當前比較常見的近鄰搜索算法。

主要算法

Kd-Tree

K-dimension tree，二叉樹結構，對數據點在k維空間（如二維 (x，y)，三維(x，y，z)，k維(x，y，z..)）中劃分。

構建過程

確定split域的值(輪詢 or 最大方差)

確定Node-data的域值（中位數 or 平均值）

確定左子空間和右子空間

遞歸構造左右子空間

查詢過程

進行二叉搜索，找到葉子結點

回溯搜索路徑，進入其他候選節點的子空間查詢距離更近的點

重復步驟2，直到搜索路徑為空

性能

理想情況下的復雜度是O(K log(N)) 最壞的情況下（當查詢點的鄰域與分割超平面兩側的空間都產生交集時，回溯的次數大大增加）的復雜度為維度比較大時，直接利用K-d樹快速檢索（維數超過20）的性能急劇下降，幾乎接近線性掃描。

改進算法

Best-Bin-First：通過設置優先級隊列（將“查詢路徑”上的結點進行排序，如按各自分割超平面與查詢點的距離排序）和運行超時限定（限定搜索過的葉子節點樹）來獲取近似的最近鄰，有效地減少回溯的次數。采用了BBF查詢機制后Kd樹便可以有效的擴展到高維數據集上。

Randomized Kd tree：通過構建多個不同方向上的Kd tree，在各個Kd tree上并行搜索部分數量的節點來提升搜索性能（主要解決BBF算法隨著Max-search nodes增長，收益減小的問題）

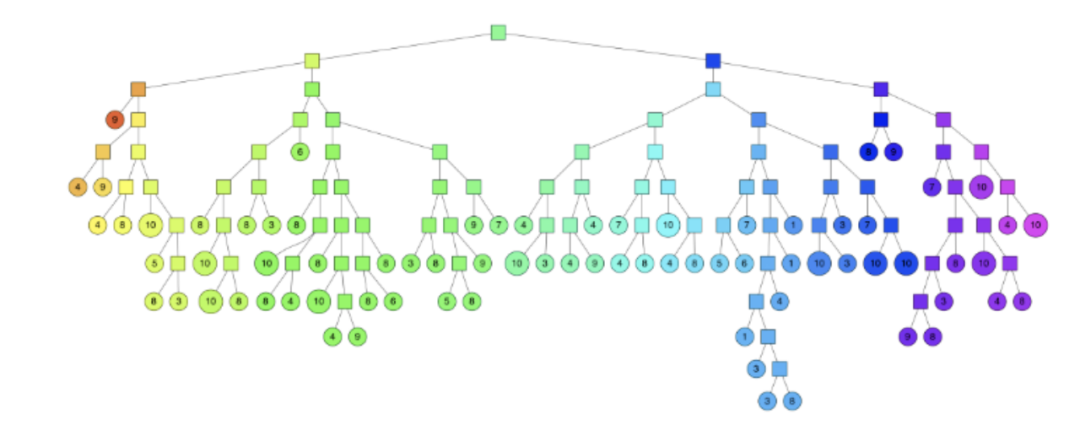
Hierarchical k-means trees

類似k-means tree，通過聚類的方法來建立一個二叉樹來使得每個點查找時間復雜度是O(log n) 。

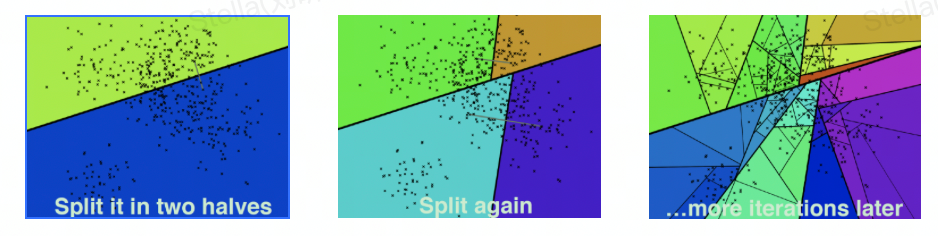
構建過程：

隨機選擇兩個點，執行k為2的聚類，用垂直于這兩個聚類中心的超平面將數據集劃分

在劃分的子空間內進行遞歸迭代繼續劃分，直到每個子空間最多只剩下K個數據節點

最終形成一個二叉樹結構。葉子節點記錄原始數據節點，中間節點記錄分割超平面的信息

搜索過程

從根節點開始比較，找到葉子節點，同時將路徑上的節點記錄到優先級隊列中

執行回溯，從優先級隊列中選取節點重新執行查找

每次查找都將路徑中未遍歷的節點記錄到優先級隊列中

當遍歷節點的數目達到指定閾值時終止搜索

性能

搜索性能不是特別穩定，在某些數據集上表現很好，在有些數據集上則有些差

構建樹的時間比較長，可以通過設置kmeans的迭代次數來優化

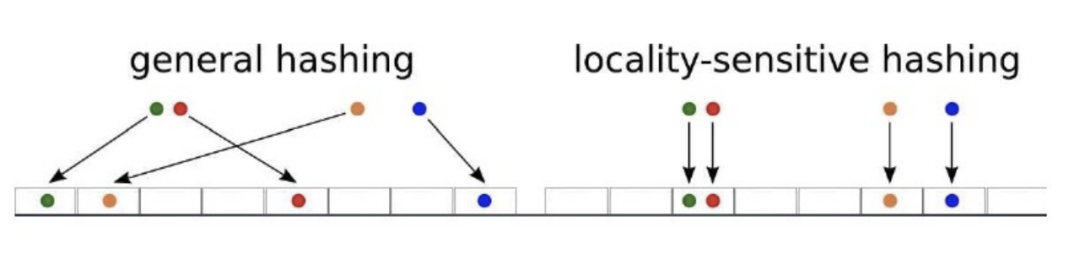
LSH

Locality-Sensitive Hashing 高維空間的兩點若距離很近，他們哈希值有很大概率是一樣的；若兩點之間的距離較遠，他們哈希值相同的概率會很小 。

一般會根據具體的需求來選擇滿足條件的hash函數，(d1,d2,p1,p2)-sensitive 滿足下面兩個條件（D為空間距離度量,Pr表示概率）：

若空間中兩點p和q之間的距離D(p,q)p1

若空間中兩點p和q之間的距離D(p,q)>d2，則Pr(h(p)=h(q))

審核編輯：劉清