01 說在前面的話

關于卡爾曼這部分內容，一直思考怎么用通俗易懂的方式來按照自己的理解梳理。但是無奈，總是繞不開用數學的方法表達那 5 個關鍵的公式。不論是在B站，還是各個博客都用很多的講解。直到理解了嚴恭敏老師在講卡爾曼濾波時的一個溫度估算舉例，才斗膽引用下面文章，來填寫卡爾曼濾波這個坑。

一個簡單的應用是估計物體的位置和速度。簡要描述如下：假設我們可以獲取一個物體的包含噪聲的一系列位置觀測數據，我們可以獲得此物體的精確速度和位置連續更新信息。例如，對于雷達來說，我們關心的是跟蹤目標，而目標的位置、速度、加速度的觀測值是時刻含有誤差的，卡爾曼濾波器利用目標的動態信息，去掉噪聲影響，獲取目標此刻好的位置估計(即濾波過程)，將來的位置估計(即預測過程)，也可以是過去位置估計的(即插值或平滑過程)。

02應用舉例

假設我們要研究的對象是一個房間的溫度。根據你的經驗判斷，這個房間的溫度是恒定的，也就是下一分鐘的溫度等于現在這一分鐘的溫度(假設我們用一分鐘來做時間單位)。 假設你對你的經驗不是絕對相信，可能會有上下偏差幾度。我們把這些偏差看成是高斯白噪聲(White Gaussian Noise，理想情況下我們以高斯噪聲來進行假設估計)，也就是這些偏差跟前后時間是沒有關系的而且符合高斯分布(Gaussian Distribution)。 另外，我們在房間里放一個溫度計，但是這個溫度計也不準確的，觀測值會比實際值偏差。我們也把這些偏差看成是高斯白噪聲。好了，現在對于某一分鐘我們有兩個有關于該房間的溫度值：你根據經驗的預測值(系統的預測值)和溫度計的值(觀測值)。下面我們要用這兩個值結合它們各自的噪聲來估算出房間的實際溫度值。 假如我們要估算k時刻的實際溫度值。首先你要根據k?1時刻的溫度值，來預測k時刻的溫度。因為你相信溫度是恒定的，所以你會得到k時刻的溫度預測值是跟k?1時刻一樣的，假設是23度，同時該值的高斯噪聲的偏差是5度(5是這樣得到的：如果k?1時刻估算出的最優溫度值的偏差是3，你對自己預測的不確定度是4度，它們平方相加再開方就是5)。 然后，你從溫度計那里得到了k時刻的溫度值，假設是25度，同時該值的偏差是4度。由于我們用于估算k時刻的實際溫度有兩個溫度值，分別是23度和25度。究竟實際溫度是多少呢?相信自己還是相信溫度計呢?究竟相信誰多一點，我們可以用它們的協方差(covariance)來判斷。因為 Kg^2=5^2/(5^2+4^2)，所以Kg=0.78，我們可以估算出k時刻的實際溫度值是：23+0.78?(25?23)=24.56度。

可以看出，因為溫度計的協方差比較小(比較相信溫度計)，所以估算出的最優溫度值偏向溫度計的值。現在我們已經得到k時刻的最優溫度值了，下一步就是要進入k+1時刻，進行新的最優估算。在進入k+1時刻之前，我們還要算出k時刻那個最優值(24.56 度)的偏差。算法如下：

這里的5就是上面的k時刻你預測的那個23度溫度值的偏差，得出的2.35就是進入k+1時刻以后k時刻估算出的最優溫度值的偏差(對應于上面的3)。就是這樣，卡爾曼濾波器就不斷的把協方差遞歸，從而估算出最優的溫度值。它運行的很快，而且它只保留了上一時刻的協方差。上面的Kg，就是卡爾曼增益(Kalman Gain)，可以隨不同的時刻而改變自己的值。

03卡爾曼濾波器算法

卡爾曼濾波基于時域描述的線性動態系統，它的模型是馬爾科夫鏈(Markov Chain)，而馬爾科夫鏈建立在一個被高斯噪聲干擾的線性算子之上。 系統的狀態可以用一個元素為實數的向量表示。隨著離散時間的增加，這個線性算子就會作用到當前狀態之上，產生一個新的狀態，并且會帶入一定的噪聲，同時一些已知的控制信息也會加入。同時，另外一個受噪聲干擾的線性算子將產生這些隱含狀態的可見輸出。卡爾曼濾波器可以被看作為類隱馬爾科夫模型，它們的顯著不同點在于：

隱狀態變量的取值空間是一個連續的空間，而不是離散的狀態空間;

另外，隱馬爾科夫模型可以描述下一個狀態的一個任意分布，這也與應用于卡爾曼濾波器中的高斯噪聲模型相反。

先看一下動態系統的基本模型。

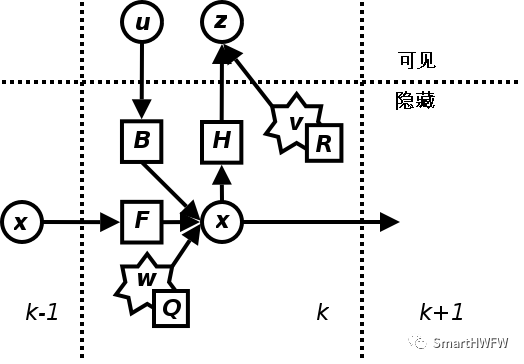
首先，我們先要引入一個離散控制過程的系統。該系統的過程模型可用一個線性隨機微分方程(Linear Stochastic Difference Equation)來描述：

再加上系統觀測模型：

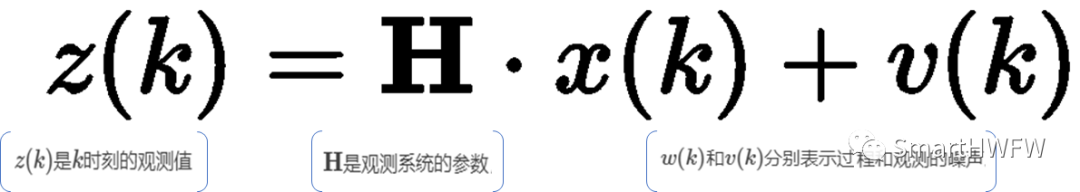
卡爾曼濾波是一種遞歸的估計，即只要獲知上一時刻狀態的估計值以及當前狀態的觀測值就可以計算出當前狀態的估計值，因此不需要記錄觀測或者估計的歷史信息。卡爾曼濾波器與大多數濾波器不同之處在于：它是一種純粹的時域濾波器，它不需要像低通濾波器等頻域濾波器那樣，需要在頻域設計再轉換到時域實現。卡爾曼濾波器的操作包括兩個階段：預測與更新：

在預測階段，濾波器使用上一狀態的估計，做出對當前狀態的估計。

在更新階段，濾波器利用對當前狀態的觀測值優化在預測階段獲得的預測值，以獲得一個更精確的新估計值。

03.1 預測階段

對于滿足上面的條件(線性隨機微分系統，過程和觀測都是高斯白噪聲)，卡爾曼濾波器是最優的信息處理器。

下面我們來用它們結合它們的協方差來估算系統的最優化輸出(類似上一節那個溫度的例子)。首先，我們要利用系統的過程模型，來預測下一狀態的系統。假設現在的系統狀態是k，根據系統的模型，可以基于系統的上一狀態而預測出現在狀態(稱為預測的狀態估計方程)：

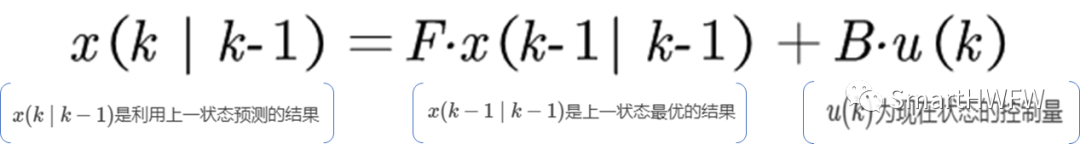
到現在為止，我們的系統結果已經更新了，可是，對應于x(k∣k?1)的協方差(covariance)還沒更新。我們用P表示協方差，它實際上描述了預測值的準確程度(稱為預測的協方差矩陣估計方程)：

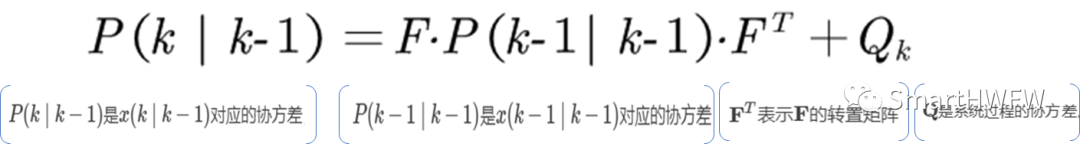
03.2 更新階段

在進行更新之前，我們先計算三個值： 首先是觀測余量(measurement residual)：

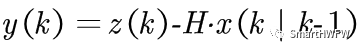
因為觀測過程中存在一個觀測誤差的協方差矩陣，我們可以給出一個觀測余量的協方差：

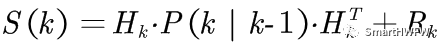
接下來給出一個卡爾曼增益(Kalman Gain)：

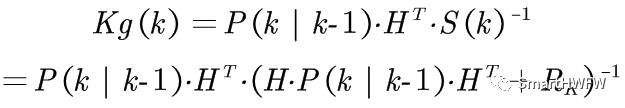
現在我們有了現在狀態的預測結果，然后我們再收集現在狀態的觀測值。結合預測值和觀測值，我們可以得到現在狀態k的最優化估算值x(k|k)(稱為更新的狀態估計方程)：

到現在為止，我們已經得到了k狀態下最優的估算值x(k∣k)。但是為了要使得卡爾曼濾波器不斷的運行下去直到系統過程結束，我們還要更新k狀態下x(k∣k)的協方差(稱為更新的協方差矩陣估計方程)：

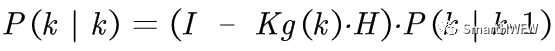
其中 I 為單位矩陣，對于單模型單觀測，I=1。當系統進入k+1狀態時，P(k∣k)就是預測方程中的P(k?1∣k?1)。這樣，算法就可以自回歸的運算下去。

03.3 算法流程抽象

1)先決定當前系統的初始狀態，并根據預測方程(過程模型)得到一個下一個時刻預測的狀態;

2)根據預測方程中過程的誤差，得到當前預測的協方差估計;

3)進入更新階段，我們根據目前系統的觀測值和上一個時刻預測的狀態，從轉換方程(觀測模型)入手，得到一個測量余量;

4)根據轉換方程和上個時刻預測的協方差估計，也可以得到一個測量余量的協方差估計;

5)根據 a)測量余量的協方差Sk∣k; b)轉換方程H和 c)上個時刻的預測協方差估計Pk∣k?1，我們得到卡爾曼增益Kk∣k;

6)根據卡爾曼增益和測量余量，我們從預測的狀態中更新優化當前的狀態的值，而這個值可以用來預測下一個時刻的狀態;

7)同樣，我們根據 a)卡爾曼增益Kk∣k 和 b)上個時刻的預測協方差估計Pk∣k?1，我們把當前更新階段的協方差Pk∣k估計也得到，幫助下一時刻的卡爾曼增益計算。

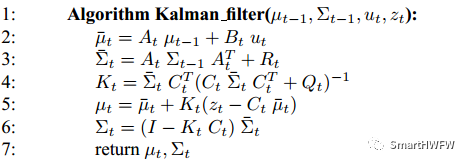
審核編輯：湯梓紅