本文介紹了射頻 (RF) 阻抗匹配的基礎知識、如何計算匹配分量以及如何檢查LTspice.
介紹
電子理論指出,當源電阻與負載電阻匹配時,最大功率從源端傳輸到負載。然而,對于大多數RF電路,源阻抗和負載阻抗具有電抗元件,在這種情況下,源阻抗必須等于負載阻抗的復數共軛,以實現最大功率傳輸。換句話說,雖然源阻抗和負載阻抗的實部必須匹配,但負載阻抗的虛部必須與源阻抗的虛部在符號上相反。
RF功率放大器電路的復雜性很大程度上是由于主要有源元件周圍的阻抗匹配元件,無論是晶體管還是集成解決方案。一旦了解了這些RF阻抗匹配電路是如何計算的,電路的其余部分就更直接了。計算這些匹配的組件是一個簡單的過程,但有時最好有一個工具來交叉檢查這些計算,并確保最大功率確實從電源傳輸到負載。
本文深入探討了Chris Bowick的《RF電路設計》一書中概述的阻抗匹配理論,許多工程師將其視為射頻圣經。讀者可能希望參考本書,以更全面地了解其他RF阻抗匹配網絡。整篇文章還包括LTspice仿真,以交叉檢查計算結果。
調諧電路和負載Q
電容器的電抗由公式1給出。

將頂部和底部乘以j意味著電容器具有負電抗。相反,電感的正電抗由公式2給出。

因此,如果我們把一個電容器和一個電感器串聯起來,它們都有 在一個特定頻率下相等但相反的電抗,它們形成一個短的 零相移電路。同樣,如果將這些組件并聯放置,它們將形成具有零相移的開路:兩個的凈阻抗 通過將阻抗的乘積除以并聯分量來找到并聯分量 它們的總和,如果它們具有相等但相反的電抗,則電抗產生 零值分母,因此是開路。
如果電阻器與電抗元件并聯或串聯放置,則 負載Q描述了電抗與電阻的比值。加載的 Q 并聯電路定義為:

串聯電路的負載Q定義為:

其中 Rp 和 Rs 是并聯和串聯電阻,Xp 和 X 是 并聯和串聯電抗。
我們可以使用網絡的加載Q將并行網絡轉換為串聯 網絡,從而使匹配變得容易得多。一次系列相當于 導出一個網絡,然后只需選擇源阻抗即可 相等的實數,但相反的虛部完成阻抗匹配。
圖1所示電路的阻抗由下式給出

其中–jXcp是并聯電容器的電抗。
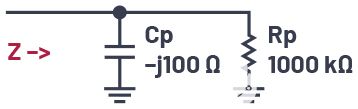
圖1.并行 CR 網絡。
該電路的串聯等效值可以通過多種方式計算。頂部和 公式5的底部可以乘以分母的復共軛,得到實數和虛部級數。或者,該方程可以 轉換為極性形式,實數和虛部分量可以是 使用正弦和余弦計算。
獲得串聯元件的更快方法是找到并行網絡的負載Q(Qp)(使用公式3),然后使用公式

以找到新系列電阻。然后,我們設計一個具有相同Q值的串聯網絡,并將新的串聯電阻Rs放入公式4中,以找到新的串聯電抗Xs。等式6的推導如附錄所示。
因此,圖1中的電路元件給出的負載Q值為10,這是通過將并聯電阻除以并聯電抗得出的。使用公式6,我們可以將并聯的1 kΩ電阻轉換為9.9 Ω的串聯電阻Rs。然后,我們可以使用公式4計算出串聯電容需要具有–j99 Ω的電抗。因此,在給定頻率下,圖1中的電路與圖2中的電路具有相同的阻抗。
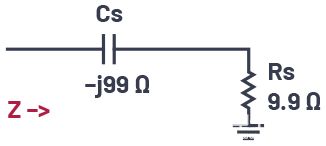
圖2.圖1所示電路的串聯表示。
由于負載的實部為9.9 Ω,負虛部(–j99 Ω),因此我們需要一個實部為9.9 Ω的源阻抗和一個正虛部(+j99 Ω),以確保實現最大的功率傳輸。實際上,通過選擇與負載電抗相等但相反的源電抗,這兩個電抗相互抵消(產生短路),我們只剩下源電阻驅動相同的負載電阻。
現在,圖2中的串聯電路僅相當于圖1中的電路。我們不必更改圖 1 的配置。如果我們使用串聯阻抗為(9.9 + j99)Ω的源驅動該并聯電路,則將傳輸最大功率。
需要注意的是,并聯電抗(在本例中為Cp)通過電路Q值確定的系數產生相當于1 kΩ電阻的較低值串聯。該電抗可以是串聯電容器或串聯電感器。反之亦然。在串聯RC電路中(如圖2所示),串聯電抗(無論是容性電抗還是電感電抗)產生串聯電阻的更高值并聯等效值Rs。實際上,我們可以重新排列公式 6 以讀取

這立即向我們表明,并聯電阻是(Q2+ 1) 倍于系列等效值。
總結前面的例子,我們可以使用并聯或串聯電抗使電阻看起來更小或更大。并聯RC網絡的負載Q值由其電阻與電抗之比決定。我們用這個負載Q將并聯網絡轉換為串聯網絡,然后選擇源阻抗的實部等于(串聯)負載阻抗的實部,然后選擇源阻抗的無功部分相等但與串聯負載阻抗的無功部分相反。
使用固定源阻抗和負載阻抗
不幸的是,我們很少能夠改變源阻抗。源阻抗和負載阻抗通常是預先確定的,因此我們必須設計一個匹配兩者的網絡
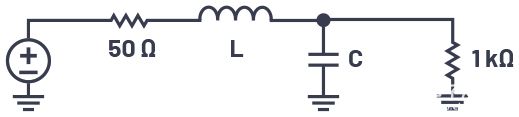
圖3.將50 Ω源與1 kΩ負載匹配,頻率為100 MHz。
圖3顯示了一個50 Ω源,需要與100 MHz時的1 kΩ負載匹配。并聯電容需要將并聯的1 kΩ轉換為串聯50 Ω電阻,這意味著該RC組合的負載Q值需要為公式6中的4.36。這將為我們提供50 Ω的等效串聯電阻加上一定值的串聯電容。然后,我們選擇一個串聯電感器,以產生與串聯電容器相等但相反的電抗。這兩個電抗抵消,我們只剩下一個50 Ω電阻饋入50 Ω負載。
我們可以使用公式3來計算并聯電容的電抗。所以

并聯電容應為6.94 pF,在100 MHz時電抗為–j229 Ω。我們現在有一個并行網絡。為了將其更改為串聯網絡,我們將并聯和串聯網絡的Q等同起來。使用公式4,我們可以看到該并聯電路轉換為Rs = 50 Ω和

所以 Xs = 218 Ω。
因此,6.94 pF電容和1 kΩ負載的并聯組合看起來像一個串聯的50 Ω電阻和一個串聯電容,電抗為–j218 Ω。選擇一個串聯電感器給出+j218 Ω可確保匹配網絡的電抗部分被取消,并且50 Ω源現在提供50 Ω的有效負載電阻。圖 4 顯示了最終網絡。
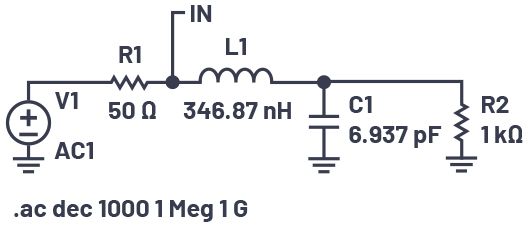
圖4.匹配元件,用于將50 Ω源與100 MHz時的1 kΩ負載匹配。
該電路可以在LTspice中仿真。電路結構正常,為方便起見,R1和L1的結點標記為“IN”。源所示,負載阻抗可以通過探測IN節點和流入L1的電流來繪制。在波形窗口中,右鍵單擊 I(L1) 并復制文本。然后右鍵單擊V(in)圖標并將文本更改為“V(in)/I(L1)”以繪制匹配網絡的輸入阻抗,如圖5所示。
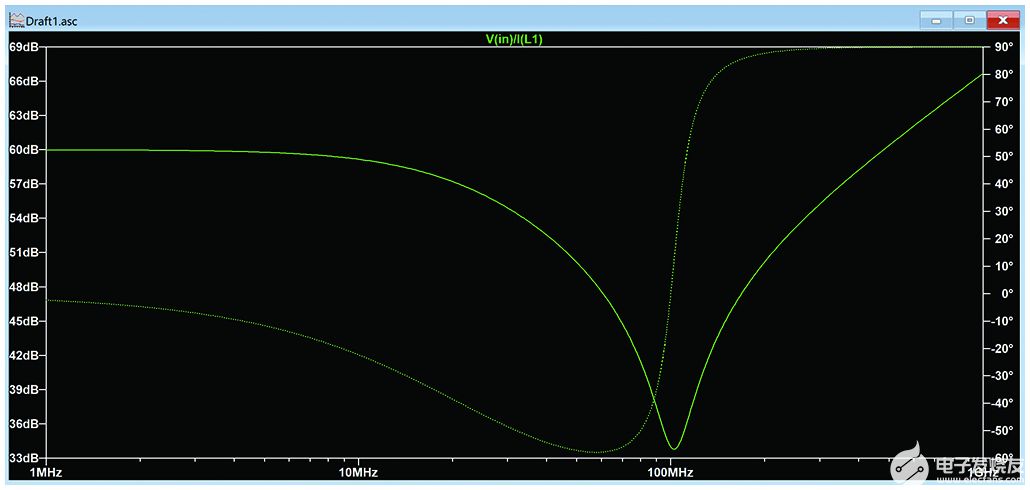
圖5.匹配網絡的輸入圖。
但是,圖5中的曲線顯示了以dB為單位的阻抗。要更改 y 軸以顯示實部和虛部,請右鍵單擊左側的 y 軸,然后將“表示”框從波特更改為笛卡爾,如圖 6 所示。
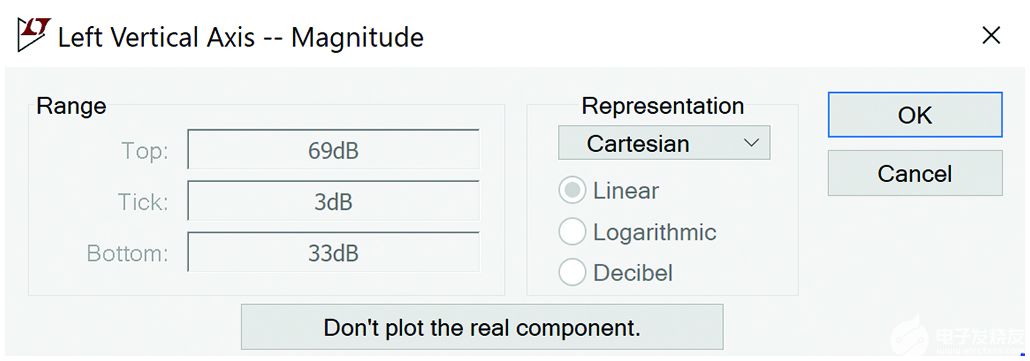
圖6.將 y 軸從波特更改為笛卡爾。
最終圖如圖7所示,實值繪制在左軸上,虛值繪制在右軸上。將光標移動到 100 MHz 位置,我們可以看到匹配網絡的輸入阻抗確實是 50 Ω,虛部很少。
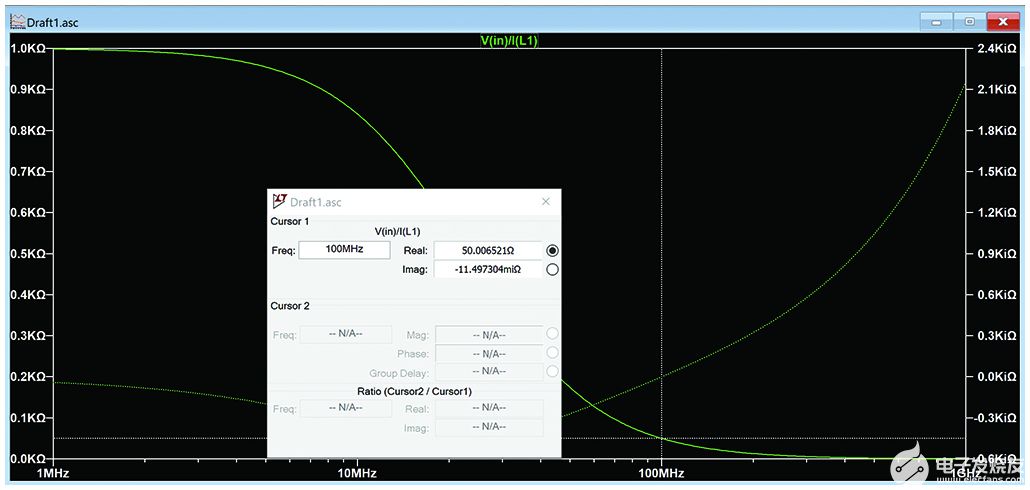
圖7.最終圖顯示了在 100 MHz 下接近 50 + j0 的匹配。
不幸的是,如果我們關閉波形窗口并重新運行仿真,我們需要重新探測V(in)和I(L1),一個除以另一個,然后更改y軸以顯示笛卡爾值。通過選擇波形窗口并選擇“文件>將圖設置另存為”,可以避免這種乏味,如圖8所示。這將保存當前波形屏幕的設置,并在下一次仿真時自動重新繪制波形。
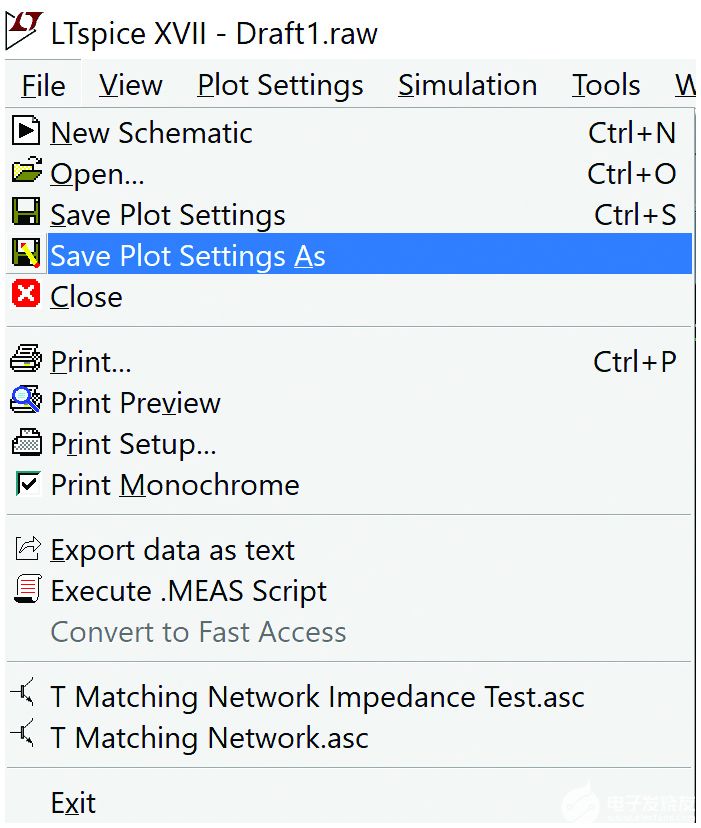
圖8.保存繪圖設置可保存 y 軸配置和繪制波形。
針對已知 Q 進行設計
在前面的示例中,我們使用并聯電容使1 kΩ負載電阻看起來像一個50 Ω串聯電阻加上一些任意串聯電容,然后選擇一個電感來抵消串聯電容的電抗。這導致了L網絡,如圖4所示。遺憾的是,圖4中的匹配網絡不允許我們選擇Q,這是由源阻抗和負載阻抗決定的。克服這個問題的一種方法是使用T網絡,如圖9所示,它由兩個背靠背的L網絡組成。
在這個例子中,我們需要使2.1 Ω負載電阻看起來像50 Ω,同時將Q保持在所需的值。為此,我們真正對串聯到并行轉換技術進行了測試。
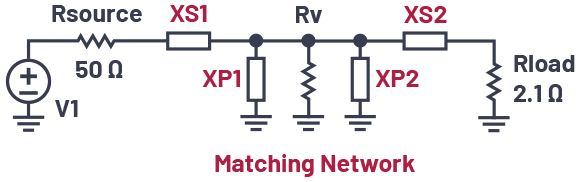
圖9.與虛擬電阻器的匹配 T 網絡。
在L網絡中,我們使用串聯電感來抵消串聯電容器的電抗(以產生短路)。在T網絡中,我們還使用并聯電感來抵消并聯電容器的電抗(以產生開路)。
查看圖9,我們知道串聯阻抗XS2(無論是電容器還是電感)將串聯2.1 Ω負載電阻轉換為更大的等效并聯電阻,加上一些任意的并聯電抗。因此,我們可以選擇XP2與該任意并聯電抗相等但相反,并產生開路。然后,我們只剩下2.1 Ω電阻器,看起來像一個更大的并聯電阻器,沒有電抗元件。
2.1 Ω負載現在看起來像一個大得多的虛擬電阻Rv,如圖9所示。請注意,電阻Rv實際上并沒有放置在電路中,我們只是使2.1 Ω電阻看起來具有更大的值,從Rv的位置來看。實際上,為了簡化電路,我們可以用Rv代替2.1 Ω電阻,XS2和XP2,從源頭觀察時,電路將在一個特定頻率下呈現相同的阻抗。
通過重新排列公式6來讀取

我們可以看到,與50 Ω的源電阻相比,該虛擬電阻越大,電路的Q值就越大。因此,我們可以修改XS2和XP2,使Rv看起來像任何值,從而得到我們想要的電路Q。然后,我們可以使用用于L網絡的方法將源阻抗(50 Ω)與負載電阻Rv相匹配。然后,我們使用XP1使Rv看起來像一個較小的串聯電阻(理想情況下為50 Ω),加上一些任意串聯電抗,我們選擇XS1相等但與該任意串聯電抗相反,因此我們剩下50 Ω源電阻饋入50 Ω負載電阻,但仍保持高Q值。
讓我們來看看方法論。我們需要將50 Ω源與100 MHz的2.1 Ω負載相匹配,所需電路Q為10。我們的目標是使圖9所示電路看起來像一個L網絡,具有50 Ω源和更大值的負載電阻Rv。我們首先需要將2.1 Ω轉換為更高值(并聯)電阻。我們知道,串聯電抗XS2將2.1 Ω轉換為更大的并聯電阻,因此從公式4

所以 XS2 = 21 Ω。
然后,我們使用公式6將該串聯電路轉換為其并聯等效電路。

所以 Rp 是 212.1 Ω。這是我們的虛擬電阻器。
因此,2.1 Ω的串聯電阻和21 Ω的串聯電抗看起來像一個更大的212.1 Ω并聯電阻加上一些任意的并聯電抗。然后,我們插入一個相等但相反的并聯電抗來抵消它以產生開路,因此我們只剩下更大的并聯電阻。為了確定并聯電抗,我們使用公式3,因此

所以 XP2 = 21.21 Ω。
如果需要,我們可以用等于212.1 Ω的單個并聯電阻代替XS2、XP2和2.1 Ω電阻,電路將在100 MHz時向源提供相同的阻抗。這可以在LTspice中模擬。該電路現在可以被視為一個簡單的L網絡,我們只需將50 Ω源電阻與212.1 Ω的負載相匹配。根據公式10,

我們需要使這個并聯的212.1 Ω電阻看起來像一個串聯的50 Ω電阻。我們知道電阻,我們知道Q,所以我們現在可以計算出實現這個Q所需的并聯電抗。插入并聯電抗將這個高值并聯電阻轉換為較低值的串聯電阻(50 Ω),加上一些串聯電抗。從公式3,

所以 XP1 = 117.8 Ω。
因此,117.8 Ω的并聯電抗使并聯212.1 Ω電阻看起來像一個50 Ω的串聯電阻。然后,我們可以使用公式4來計算串聯電抗。
并聯電抗為117.8 Ω,電阻為212.1 Ω,Q為1.80。將其轉換為具有相同Q值和50 Ω串聯電阻的串聯電路,使我們能夠計算串聯電抗。
從公式4,

212.1 Ω的并聯電阻和117.8 Ω的電抗看起來像50 Ω的串聯電阻加上90 Ω的電抗。如果 X小一是一個電容器,這轉化為串聯電容(電抗 –J90 Ω),因此串聯匹配分量必須是感性的(電抗 +J90 Ω),因此電抗抵消。
從上述過程中有幾點需要注意。首先,對于T網絡,設計從電路末端使用最低值電阻開始,在上面的例子中,電阻是2.1 Ω,而不是50 Ω。從公式6可以看出,如果我們從50 Ω端開始,我們將計算出更高的Rv值,并且由于負載電阻低得多,為2.1 Ω,最終網絡的右半部分具有巨大的Q值。其次,我們注意到串聯電抗總是與并聯電抗相反的符號,因為我們需要確保它們相互抵消。因此,串聯電容器通常需要并聯電感器,反之亦然。
組件值如表1所示。
| 元件 | 阻抗 | 100 MHz 時的組件值 |
| XS1 | 90 | 17.68 點頻 |
| 是的 | 117.8 | 187.5 千兆安時 |
| XS2 | 21 | 75.79 點頻 |
| XP2 | 21.21 | 33.76 千兆安時 |
由于XP1和XP2是并聯電感,因此可以組合成一個電感器 電感器,值為 28.61 nH。最終電路如圖10所示。
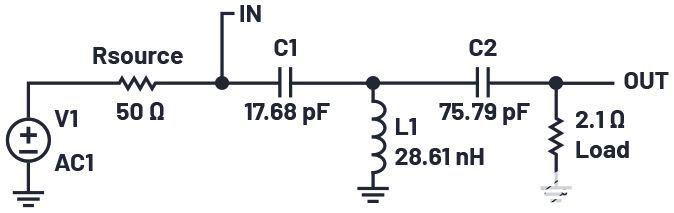
圖 10.完整的 T 網絡。
繪制IN節點的電壓并將其除以流入C1的電流,我們可以看到匹配網絡的輸入阻抗非常接近50 Ω,如圖11所示。
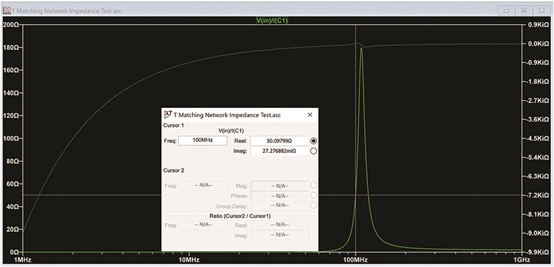
圖 11.100 MHz 時的輸入阻抗圖。
我們還可以通過繪制負載兩端的電壓和流過負載的電流并逐一相乘來繪制傳輸到負載的功率,如圖12所示。
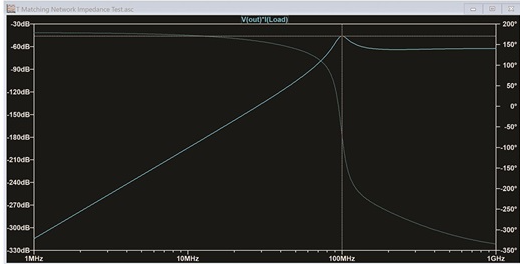
圖 12.最大功率以 100 MHz 傳輸。
通過右鍵單擊繪圖窗口并選擇添加繪圖窗格,我們可以在一個窗口中同時繪制匹配,在另一個窗口中繪制功率傳輸。保存繪圖設置可確保在每次仿真后自動繪制這些設置。
處理復雜負載
負載很少是純電阻性的。如果圖10中的2.1 Ω負載具有398 pF的串聯電容元件(在100 MHz時等于–j4.0 Ω),則會破壞匹配網絡。但是,這很容易克服。在圖10中,C2和2.1 Ω負載形成一個串聯網絡,其Q值為10,由電抗(–j21 Ω)與電阻(2.1 Ω)之比決定。額外的–j4.0 Ω將總電抗增加到–j25 Ω。為了保持相同的Q值,我們需要在該串聯組合中增加一個正電抗,以消除負載的–j4.0 Ω。這可以通過在與C2串聯時增加6.37 nH的電感(電抗為+j4.0 Ω)來實現,以保持電抗與電阻的比值。更方便的方法是將電容C2的值增加到93.62 pF。這會將電抗降低到–j17 Ω,然后負載電容將凈串聯電抗增加回–j21 Ω,從而保持Q為10。LTspice可用于提供健全性檢查,最終電路如圖13所示。
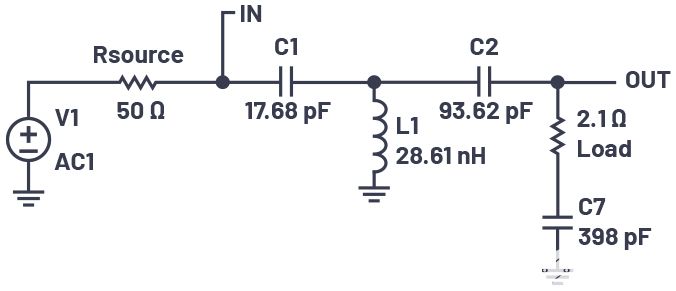
圖 13.與復雜負載匹配的修訂后的 T 網絡。
圖14顯示,該電路在100 MHz時與50 Ω具有良好的匹配,并傳輸最大功率。
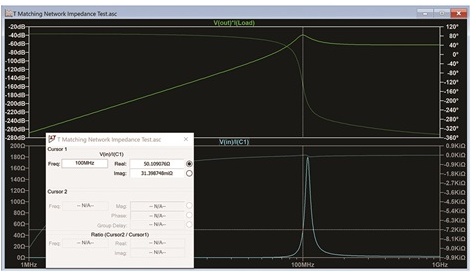
圖 14.100 MHz 復數負載下的功率輸出和輸入阻抗圖。
結論
希望本文揭開了RF阻抗匹配的神秘面紗,并使RF功率放大器電路更易于理解。使用網絡的負載Q值,我們可以在串聯和并聯網絡之間切換,并將低值電阻轉換為高值電阻。然而,與任何工程任務一樣,對計算進行交叉檢查總是好的,LTspice在繪制電路的輸入阻抗和功率輸出方面證明是無價的。
審核編輯:郭婷
-
電容器
+關注
關注
64文章
6256瀏覽量
100249 -
射頻
+關注
關注
104文章
5620瀏覽量
168230 -
電感器
+關注
關注
20文章
2335瀏覽量
70771
發布評論請先 登錄
相關推薦
阻抗匹配設計的實現
基于Ansoft Designer的射頻功放電路阻抗匹配優化
怎樣理解阻抗匹配_pcb阻抗匹配如何計算

阻抗匹配的原理及應用
射頻(RF)阻抗匹配:計算和仿真





 射頻阻抗匹配:計算和仿真
射頻阻抗匹配:計算和仿真
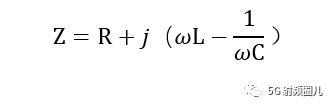










評論