摘要

深度網絡在從大量數據中學習模式方面表現出色。另一方面，許多幾何視覺任務被指定為優化問題。

為了將深度學習和幾何視覺無縫地結合起來，至關重要的是進行端到端的學習和幾何優化。

為了實現這一目標，我們提出了BPnP，這是一個新穎的網絡模塊，通過Perspective-nPoints（PnP）求解器反向傳播梯度，以指導神經網絡的參數更新。

基于隱式微分，我們表明一個 "獨立的 "PnP求解器的梯度可以被準確有效地導出，就像優化器塊是一個可微分的函數。

我們通過將BPnP納入一個深度模型來驗證它，該模型可以從訓練數據集中學習相機的內在因素、相機的外在因素（姿勢）和三維結構。

此外，我們開發了一個用于物體姿勢估計的端到端可訓練管道，該管道通過將基于特征的熱圖損失與二維-三維重投影誤差相結合，實現了更高的準確性。

由于我們的方法可以擴展到其他優化問題，我們的工作有助于以一種原則性的方式實現可學習的幾何視覺。

主要貢獻

我們的主要貢獻是一個名為BPnP的新型網絡模塊，它包含了一個PnP求解器。BPnP通過PnP "層 "反向傳播梯度，以指導神經網絡權重的更新，從而利用既定的目標函數（二維-三維重投影誤差的平方和）和幾何視覺問題的求解器實現端到端的學習。

盡管只結合了一個PnP求解器，我們展示了BPnP如何被用來學習有效的深度特征表征，用于多種幾何視覺任務（姿勢估計、運動結構、相機校準）。

我們還將我們的方法與最先進的幾何視覺任務的方法進行比較。從根本上說，我們的方法是基于隱式微分的。

主要方法

反向傳播的PnP算法： 讓g表示一個 "函數 "形式的PnP求解器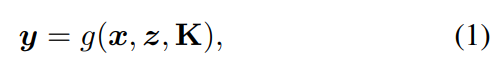



從n個2D-3D的對應關系中返回攝像機的6DOF姿態y和其內部參數K∈R3×3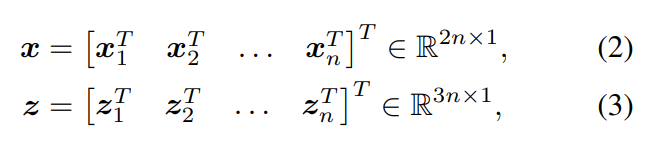



其中(xi , zi)是第i個對應關系。讓π(-|y, K)是三維點在圖像平面上的投影變換，姿態為y，相機本征為K。

從本質上講，g的 "評估 "需要解決優化問題如下：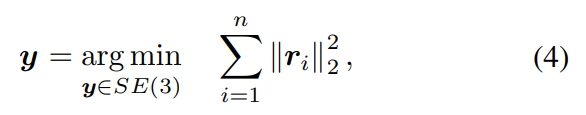





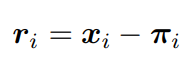
ri表示第i對對應關系的重投影誤差。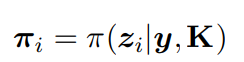



πi是三維點zi在圖像平面上的投影。

我們的最終目標是將g納入一個可學習的模型中，其中x、z和K可以是一個深度網絡的（中間）輸出。此外，公式（4）的求解器應該被用來參與網絡參數的學習。為此，我們需要把g當作一個可微調的函數，這樣它的"梯度 "就可以反向傳播到網絡的其他部分。接下來我們將詳細介紹如何對反向傳播的梯度進行計算。

1. 隱式函數定理（IFT） 這里簡單公式推導了IFT隱式函數定理。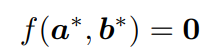







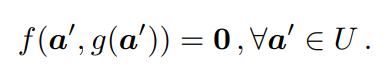
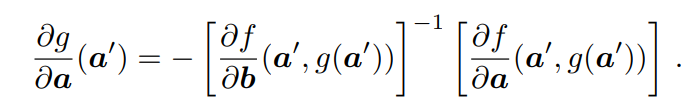
IFT允許計算一個函數g相對于其輸入a的導數，而不需要函數的明確形式，但有一個函數f約束a和g(a)。

2. 構造約束函數f

為了調用隱式微分的IFT，我們首先需要定義約束函數f(a, b)。對于我們的問題，我們使用所有四個變量x、y、z和K來構造f。

但我們將f視為一個雙變量函數f(a, b)，其中a在{x, z, K}中取值--取決于要得到的偏導--而b=y（即g的輸出姿勢）。

為了維護約束函數f(a,b)，我們利用了優化過程的靜止約束。

在這里，將PnP求解器的目標函數g表示為：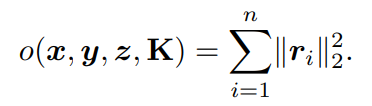



由于PnP求解器的輸出姿態y是目標函數的局部最優，所以可以通過對目標的一階導數與y的關系來建立一個靜止約束，即：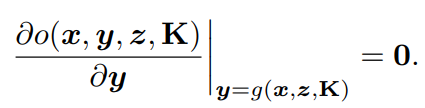



給出一個PnP求解器的輸出姿勢y = [y1, ..., ym] T，我們構建f，可以寫為：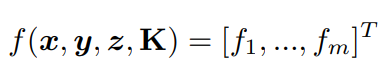





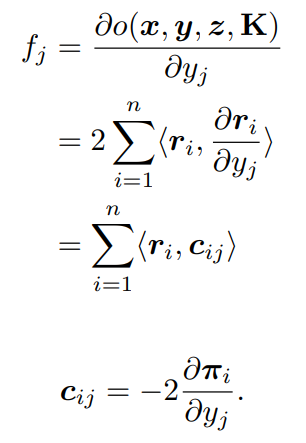
3. 前向和反向傳播

我們對g的PnP公式基本上是執行最小二乘法（LS）估計，這對離群值（x、z和K的惡劣誤差）并不穩健。

另外，我們可以采用一個更穩健的目標，如加入M-估計器[56]或使離群值的數量最大化[15]。

然而，我們的結果表明，LS實際上更合適，因為它對輸入測量中的誤差的敏感性鼓勵學習快速收斂到不產生x、z和K中的異常值的參數。

相反，一個穩健的目標會阻止異常值的誤差信號，導致學習過程不穩定。

鑒于（4），解算器的選擇仍然存在。

為了進行隱式微分，我們不需要精確地解決（4），因為cij只是（4）的靜止條件，任何局部最小值都能滿足。

為此，我們采用Levenberg-Marquardt（LM）算法，該算法保證了局部收斂。

作為一種迭代算法，LM在求解（4）時需要初始化y（0）。

我們通過將(1)重寫為："(1)"來明確這種依賴關系：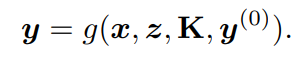



在反向傳播中，我們首先構建f，然后得到g相對于其每個輸入的雅可比系數，即：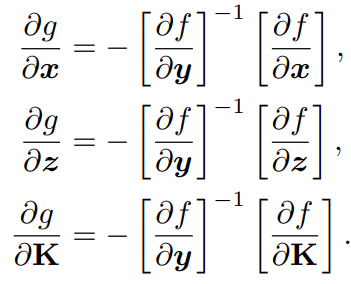



給出輸出梯度，BPnP返回輸入梯度：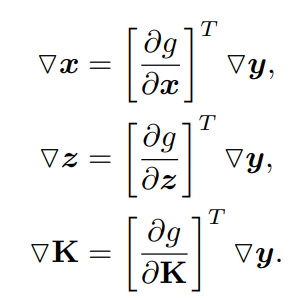



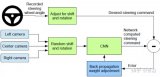
算法流程如下圖所示：



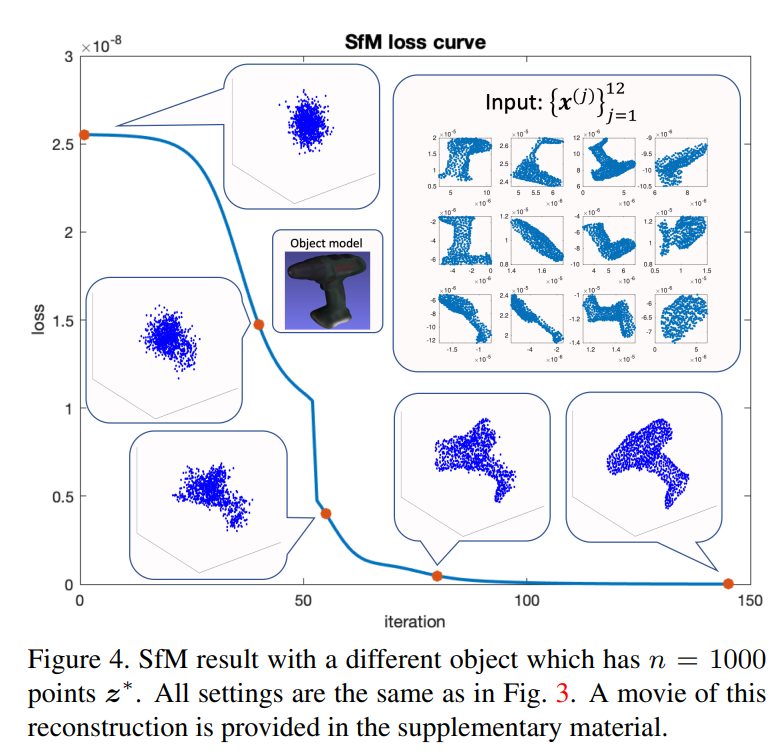
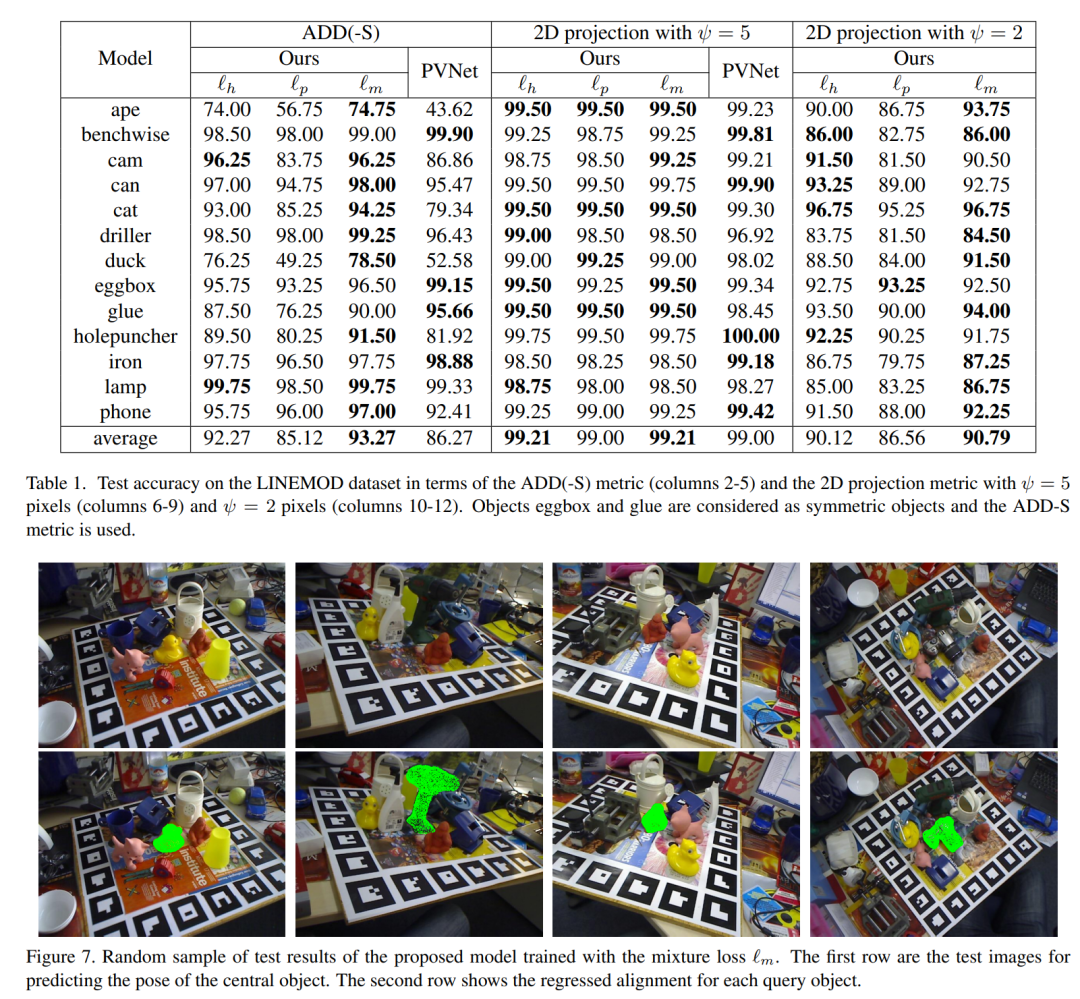
主要結果：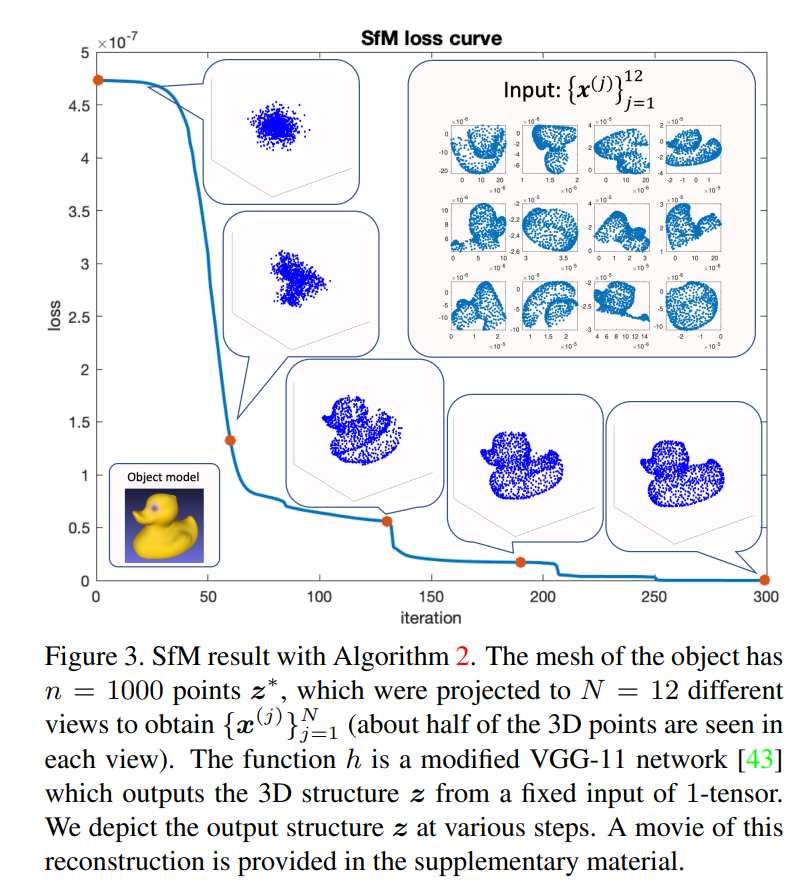










審核編輯：劉清