根據(jù)牛頓定律,運(yùn)動(dòng)物體總是有趨于靜止,或保持運(yùn)動(dòng)的特性,我們把物體所具有的這種狀態(tài),叫做穩(wěn)態(tài),與此相反的非穩(wěn)態(tài),叫做瞬態(tài),瞬態(tài)是反應(yīng)物體變化過(guò)程的模型。
在數(shù)字電路設(shè)計(jì)中,到達(dá)0或1這兩種穩(wěn)態(tài)的過(guò)程,實(shí)際上是連續(xù)的,而我們把它當(dāng)做是離散信號(hào),一個(gè)離散信號(hào),可以看做是一個(gè)連續(xù)信號(hào)在跳變瞬間的時(shí)間增量為無(wú)窮小,即: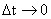 ,通常我們不考慮這個(gè)連續(xù)過(guò)程,但在產(chǎn)品的穩(wěn)定性和可靠性設(shè)計(jì)上,必須要考慮這個(gè)問(wèn)題,即離散信號(hào)的連續(xù)特性,或者說(shuō)瞬態(tài)。
,通常我們不考慮這個(gè)連續(xù)過(guò)程,但在產(chǎn)品的穩(wěn)定性和可靠性設(shè)計(jì)上,必須要考慮這個(gè)問(wèn)題,即離散信號(hào)的連續(xù)特性,或者說(shuō)瞬態(tài)。
設(shè)某一精密電源,其額定輸出為24V240w,考慮到,上電瞬間對(duì)母電源的沖擊,引起其它單元模塊的電壓波動(dòng),我們需要適當(dāng)限制其瞬間沖擊功率,待到電路基本穩(wěn)定時(shí),再馬力全開。
設(shè)某一RC電路,如下圖所示。
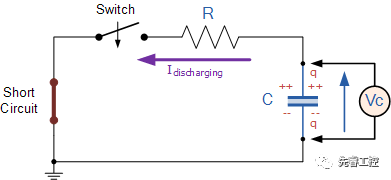
在該電路中,由電壓模型,我們得知:
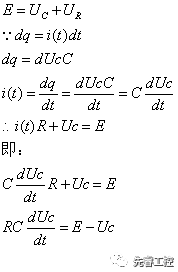
解此微分方程:

解,設(shè),當(dāng)電源電壓為24V,電阻為100歐姆,電容為4700uf X2 則,代入上式,得電壓與時(shí)間的函數(shù)關(guān)系如下圖所示。
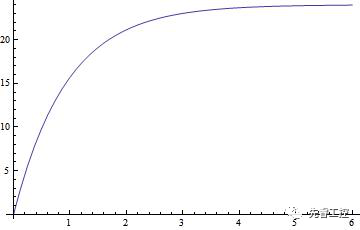
設(shè),設(shè)計(jì)某一電路,當(dāng)電容充電至18伏時(shí),全功率開啟,則t=?

即,在上電之后 ,經(jīng)過(guò)1.3秒時(shí)間,電壓上升至18伏。
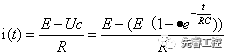
將以上解代入原式,得電流與時(shí)間的函數(shù)關(guān)系如下圖所示。
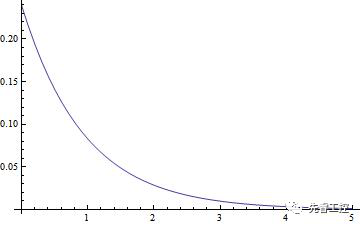
當(dāng)我們把電流放大100倍時(shí),函數(shù)關(guān)系如上。
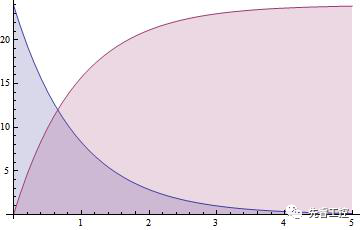
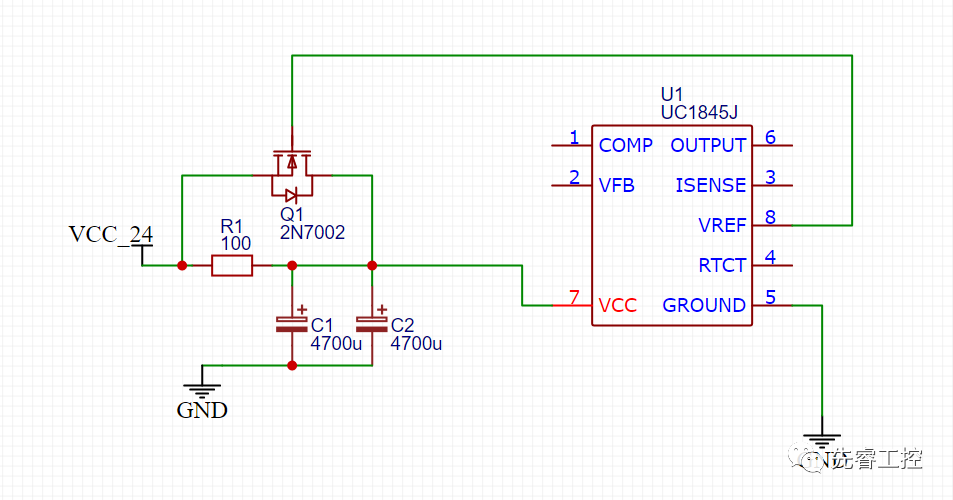
根據(jù)上述方程的解,當(dāng)我們?cè)O(shè)計(jì)一個(gè)電源,如下圖所示,確定合適的R1,C1,C2的值,就可以起到防沖擊作用,反之,大容量電容所引起的瞬間沖擊是不容小窺的事。
先睿工控:恭祝大家新春愉快,萬(wàn)事如意,闔家歡樂(lè)!
聲明:本文內(nèi)容及配圖由入駐作者撰寫或者入駐合作網(wǎng)站授權(quán)轉(zhuǎn)載。文章觀點(diǎn)僅代表作者本人,不代表電子發(fā)燒友網(wǎng)立場(chǎng)。文章及其配圖僅供工程師學(xué)習(xí)之用,如有內(nèi)容侵權(quán)或者其他違規(guī)問(wèn)題,請(qǐng)聯(lián)系本站處理。
舉報(bào)投訴
相關(guān)推薦
dsp數(shù)字信號(hào)處理
電子技術(shù)那些事兒
發(fā)布于 :2022年08月27日 20:06:12
微分方程經(jīng)典求解法 一個(gè)線性系統(tǒng),其激勵(lì)信號(hào) &
發(fā)表于 09-10 12:23
Matlab偏微分方程工具箱應(yīng)用說(shuō)明1. 概述本文只給出該工具箱的函數(shù)列表,讀者應(yīng)先具備偏微分方程的基本知識(shí),然后根據(jù)本文列出的函數(shù)查閱Matlab的幫助,便可掌握該工具箱的使用。2. 偏微分方程
發(fā)表于 09-22 15:26
本帖最后由 A670521546 于 2011-7-8 10:29 編輯
常微分方程(ODEs)的MATLAB數(shù)值解法》偏微分方程(PDEs)的MATLAB數(shù)值解法》Z變換和差分方程
發(fā)表于 07-08 08:42
哪位大俠擅長(zhǎng)做matlab數(shù)值計(jì)算,主要是微分方程組的求解,可以盡快聯(lián)系我,必有重謝。qq631467039
發(fā)表于 02-26 17:03
如何列寫控制系統(tǒng)微分方程?列寫控制系統(tǒng)微分方程注意事項(xiàng)有哪些?
發(fā)表于 10-25 06:12
【全美經(jīng)典】微分方程 第二版
發(fā)表于 08-08 14:57
?0次下載
摘要:對(duì)一些不能求解解析解的常微分方程和偏微分方程進(jìn)行精確求解是非常困難的,探討了用MATLAB方法對(duì)此類方程進(jìn)行求解,結(jié)合實(shí)例介紹了MATLAB數(shù)值計(jì)算的方法,先將物體的運(yùn)
發(fā)表于 01-08 21:24
?61次下載
研究了一類含有“一般”時(shí)延的高階泛函微分方程的周期解問(wèn)題,將原方程化為等價(jià)的泛函微分方程,并利用該等價(jià)泛函微分方程的特征方程,得到了原
發(fā)表于 02-28 17:07
?15次下載
常微分方程復(fù)習(xí),常微分方程pdf:微分方程的一般概念線性常微分方程的性質(zhì)一階線性常微分方程二階線性常系數(shù)
發(fā)表于 04-23 22:08
?0次下載
導(dǎo)熱微分方程式視頻教程
發(fā)表于 07-05 19:28
?37次下載

微分方程式的建立與求解:復(fù)習(xí)求解系統(tǒng)微分方程的經(jīng)典法物理系統(tǒng)的模型微分方程的列寫n 階線性時(shí)不變系統(tǒng)的描述求解系統(tǒng)微分方程的經(jīng)典法一.物理系統(tǒng)的模型
發(fā)表于 09-30 19:30
?0次下載
對(duì)于高階線性微分方程,各教材均有系統(tǒng)的求解方法 .而對(duì)于一般高階非線性微分程,由于沒(méi)有系統(tǒng)的解法,故有關(guān)微分方程的專門教材也未給與更多的介紹.而僅僅對(duì)一些較為特
發(fā)表于 03-03 22:12
?24次下載
摘要:提出在高階電路中運(yùn)用狀態(tài)方程求解各個(gè)變量的具體方法和步驟,以便于應(yīng)用計(jì)算機(jī)分析電路。其優(yōu)點(diǎn)是比求解高階微分方程要容易得多, 尤其是用數(shù)值法在計(jì)算機(jī)上求解時(shí)
發(fā)表于 04-29 08:53
?20次下載
微分、積分和微分方程4.1. 知識(shí)要點(diǎn)和背景:微積分學(xué)基本定理 4.2 實(shí)驗(yàn)與觀察(Ⅰ):數(shù)值微積分4.2.1實(shí)驗(yàn):積分定義、微分
發(fā)表于 10-17 00:32
?4604次閱讀
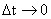 ,通常我們不考慮這個(gè)連續(xù)過(guò)程,但在產(chǎn)品的穩(wěn)定性和可靠性設(shè)計(jì)上,必須要考慮這個(gè)問(wèn)題,即離散信號(hào)的連續(xù)特性,或者說(shuō)瞬態(tài)。
,通常我們不考慮這個(gè)連續(xù)過(guò)程,但在產(chǎn)品的穩(wěn)定性和可靠性設(shè)計(jì)上,必須要考慮這個(gè)問(wèn)題,即離散信號(hào)的連續(xù)特性,或者說(shuō)瞬態(tài)。
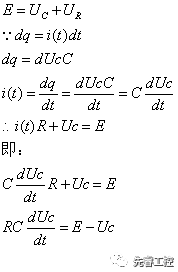



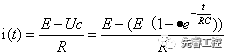








 分析微分方程
分析微分方程











評(píng)論