機器數和真值
機器數
一個數在計算中的二進制表示形式,叫做這個數的機器數,機器數是帶符號的,正數為0,負數為1。
如 :
- 十進制數+3,機器數就是00000000000000000000000000000011
- 十進制數-3,那機器數不就是10000000000000000000000000000011 ,想當然~ 實際是11111111111111111111111111111101,這個數是-3的補碼形式,因為負數在機器中是以補碼的形式存在的。
真值
真正數學意義上的數值。因為第一位是符號位,所以機器數形式值就不等于真正的數值。 如:
00000000000000000000000000000011->+3
11111111111111111111111111111101->-3
當然前面的舉例是針對有符號數來說的,對于無符號數,機器數和真值是一致的。
無符號數和有符號數機器數和真值換算方式
無符號數換算:
用一個函數 B2Uw (Binary to Unsigned)的縮寫,長度為w來表示:
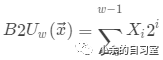
如4位二進制數:




有符號數換算方式
前面我們說過有符號數在計算機中的機器數是以補碼的形式存在的,其換算公式 B2Tw (Binary to Two`s complement):

如下面4位二進制數:




當然還有一種大眾所知的方式:就是使用原碼,反碼,補碼變換規律
原碼,反碼,補碼
計算機機器數運行效率問題
首先要清楚我們計算機中統一使用的是加法計算,對你沒聽錯。。計算機居然不會減法,哈哈。
在補碼概念提出之前,我們來舉幾個例子:

可以看到在有負數參與的加法計算得到的結果是有誤的。
如果需要得到正確的結果,計算器不得不是有其他方式去得到,這樣必然就會影響運行效率。
為了解決負數在計算機中運行效率問題,科學家們提出了補碼的概念。
補碼:
使用補碼獲取真值
那如何使用補碼規則獲取一個負數的真值呢?

假設我們從計算中獲取了一個二進制為10000001的8位機器數,如何獲取其真值。
- step1 .首先10000001是指一個補碼形式機器數,實際上在計算機系統中,所有的整數都是以補碼的形式存在,包括正數和負數,正數的補碼就是原碼自己所以統一使用補碼來存儲。
- step2 .按照補碼到反碼規則,在補碼10000001基礎上-1,將得到反碼:10000000
- step3 .按照反碼到原碼規則,將符合位不變,反碼取反即可得原碼:11111111
- step4 .按照原碼的真值概念:原碼的符合位為符號位,不參與計算,其他位為真值的絕對值即可:- 127

補碼的計算邏輯
我們回到前面分析運行效率時舉的正正,負負,正負相加例子:
這里我們使用補碼再來計算下:

可以看出,將符號以補碼的形式存儲在計算機中之后就可以使用加法來代替減法的操作,大大提高了計算機的運行效率。
補碼的設計來源
通過文章前半部分介紹,相信你已經對補碼有了一個比較全面的概念了,但是補碼是怎么設計出來的呢?
數學里面有一個“補數”概念。
補數
生活中有很多例子,只要是 帶周期性的事務性質的都可以用補數來形容 。比如:時鐘或者轉盤等。

假設當前時間是2點,你要讓時鐘顯示到12點,那么有兩個方式。
- 方式1 .將指針順時針撥動10個點,做的是 加法 :+10。
- 方式2 .將指針逆時針撥動2個點,做的是 減法 :-2。
對于時鐘來說,不管你是方式1的加法運行還是方式2的減法運算,指針都指向了12點,實現的效果是一致的, 那我們就說+10和-2是兩個補數,它們的絕對值之和12就是補數的模 。
這種規律也被應用到計算機二進制中 。下面我們使用一個例子來看:
假設要計算:(5)+(-1) = 5+(+?)
- 5在計算機中的原碼: 0 0 0 0 0 1 0 1
- -1在計算機中的原碼:1 0 0 0 0 0 0 1
要將這個減法操作變為加法操作,首要任務就是找到模,然后得到-1的正補數相加即可 。
來看我們的時鐘,每撥動12格為一個周期,就是說復原了,一樣的, 8bit位范圍是-128~127 ,(注意這里我們為了精簡分析使用的是8位來測試計算,實際計算機中場景一般都是32位格式4個字節或者64位計算)所以 其一個周期就是256,也就是其模就是256 (1 0000 0000),不管你是加上256還是減少256,在二進制中,值都是不變的,因為最后一位是溢出位,不會去計算。
通過以上分析我們找到了-1(1 0 0 0 0 0 0 1)的模為256(1 0000 0000),-1的補數為(+255):0 1111 1111
這樣就將5-1這個減法運算變更為了5+255這個加法操作
下面我們來看5+255:
5:0000 0101
255:0 1111 1111
二進制相加后:1 0000 0100 ->最高位溢出丟棄所以結果為4.
看到是不是和5-1結果一樣呢?。
其實計算機中的補碼也是這個模式: 找到一個與負數等價的正補數,使用該正補數代替負數,從而將減法運算替換為兩個正數加法運算 ,補碼的出現與運算器的電路設計有關,從設計者的角度看,希望盡可能簡化電路設計和計算復雜度。而使用正補數代替負數就可以消除減法器,實現簡化電路的目的。
我們下期見。
參考:為什么計算機中的負數要用補碼表示?
-
二進制
+關注
關注
2文章
796瀏覽量
41757 -
計算機
+關注
關注
19文章
7540瀏覽量
88643 -
十進制
+關注
關注
0文章
67瀏覽量
13283 -
補碼
+關注
關注
0文章
14瀏覽量
7570
發布評論請先 登錄
相關推薦
計算機中原碼,反碼,補碼之間的關系
在計算機中不同硬件對Hz的定義相同嗎
微型計算機中采用的邏輯元件是什么
單片機的重要功能/組成
計算機的原碼與反碼及其補碼是干啥的?
從5個方面來解析計算機中的字符編碼概念

整數如何在計算機中表示





 計算機中的負數要用補碼來表示?
計算機中的負數要用補碼來表示?
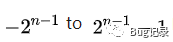










評論