現在寫滑動窗口算法的時機應該是合適的,因為讀者已經通過 [雙指針技巧匯總]理解了雙指針的套路,通過 [單調隊列解決滑動窗口問題]對滑動窗口這個東西有了個印象,而且通過 [一個方法團滅股票問題] 看到了成體系方法舉一反三的威力。
本文詳解「滑動窗口」這種高級雙指針技巧的算法框架,帶你秒殺幾道高難度的子字符串匹配問題。
LeetCode 上至少有 9 道題目可以用此方法高效解決。但是有幾道是 VIP 題目,有幾道題目雖不難但太復雜,所以本文只選擇點贊最高,較為經典的,最能夠講明白的三道題來講解。第一題為了讓讀者掌握算法模板,篇幅相對長,后兩題就基本秒殺了。文章最后抽象出一個簡單的算法框架。
本文代碼為 C++ 實現,不會用到什么編程方面的奇技淫巧,但是還是簡單介紹一下一些用到的數據結構,以免有的讀者因為語言的細節問題阻礙對算法思想的理解:
unordered_map 就是哈希表(字典),它的一個方法 count(key) 相當于 containsKey(key) 可以判斷鍵 key 是否存在。
可以使用方括號訪問鍵對應的值 map[key]。需要注意的是,如果該 key 不存在,C++ 會自動創建這個 key,并把 map[key] 賦值為 0。
所以代碼中多次出現的 map[key]++ 相當于 Java 的 map.put(key, map.getOrDefault(key, 0)+1)。
PS:本文大的主要代碼都是圖片形式,可以點開放大,更重要的是可以左右滑動方便對比代碼。
一、最小覆蓋子串

題目不難理解,要求在串 S(source) 中找到包含串 T(target) 中全部字母的一個子串,順序無所謂,但這個子串得是所有可能子串中最短的。
此題難度 Hard,但是因為很有代表性,所以放到第一道。
如果我們使用暴力解法,代碼大概是這樣的:
for (int i = 0; i < s.size(); i++)
for (int j = i + 1; j < s.size(); j++)
if s[i:j] 包含 t 的所有字母:
更新答案
思路很直接吧,但是顯然,這個算法的復雜度肯定大于 O(N^2) 了,不好。
滑動窗口算法的思路是這樣:
1 、我們在字符串 S 中使用雙指針中的左右指針技巧,初始化 left = right = 0,把索引閉區間 [left, right] 稱為一個「窗口」。
2 、我們先不斷地增加 right 指針擴大窗口 [left, right],直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
3 、此時,我們停止增加 right,轉而不斷增加 left 指針縮小窗口 [left, right],直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同時,每次增加 left,我們都要更新一輪結果。
4 、重復第 2 和第 3 步,直到 right 到達字符串 S 的盡頭。
這個思路其實也不難, 第 2 步相當于在尋找一個「可行解」,然后第 3 步在優化這個「可行解」,最終找到最優解。 左右指針輪流前進,窗口大小增增減減,窗口不斷向右滑動。
下面畫圖理解一下,needs 和 window 相當于計數器,分別記錄 T 中字符出現次數和窗口中的相應字符的出現次數。
初始狀態:

增加 right,直到窗口 [left, right] 包含了 T 中所有字符:

現在開始增加 left,縮小窗口 [left, right](此時窗口里的字符串是最優解):

直到窗口中的字符串不再符合要求,left 不再繼續移動:

之后重復上述過程,再移動 right 試圖使窗口中的字符再次符合要求,之后移動 left 縮小窗口… 直到 right 指針到達字符串 S 的末端,算法結束。
在算法執行過程中,就可以找到長度最短符合條件的子串(窗口)。
如果你能夠理解上述過程,恭喜,你已經完全掌握了滑動窗口算法思想。至于如何具體到問題,如何得出此題的答案,都是編程問題,很容易解決。
上述過程可以簡單地寫出如下偽碼框架:
string s, t;
// 在 s 中尋找 t 的「最小覆蓋子串」
int left = 0, right = 0;
string res = s;
// 先移動 right 尋找可行解
while(right < s.size()) {
window.add(s[right]);
right++;
// 找到可行解后,開始移動 left 縮小窗口
while (window 符合要求) {
// 如果這個窗口的子串更短,則更新結果
res = minLen(res, window);
window.remove(s[left]);
left++;
}
}
return res;
如果上述代碼你也能夠理解,那么你離解題更近了一步。現在就剩下一個比較棘手的問題:
如何判斷 window 即子串 s[left...right] 是否符合要求,即是否包含 t 的所有字符呢?
可以用兩個哈希表當作計數器解決。用一個哈希表 needs 記錄字符串 t 中包含的字符及出現次數,用另一個哈希表 window 記錄當前「窗口」中包含的字符及出現的次數。如果 window 包含所有 needs 中的鍵,且這些鍵對應的值都大于等于 needs 中的值,那么就可以知道當前「窗口」符合要求了,可以開始移動 left 指針了。
現在將上面的框架繼續細化:

上述代碼已經具備完整的邏輯了,只有一處偽碼,即更新最短子串結果 res 的地方,不過這個問題太好解決了,直接看完整解法吧!

如果直接甩給你這么一大段代碼,我想你的心態是爆炸的。但是通過之前的步步跟進,你應該能夠理解這個算法的內在邏輯,能清晰看出該算法的結構了。
這個算法的時間復雜度是 O(M + N),M 和 N 分別是字符串 S 和 T 的長度。因為我們先用 for 循環遍歷了字符串 T 來初始化 needs,時間 O(N),之后的兩個 while 循環最多執行 2M 次,時間 O(M)。
讀者也許認為嵌套的 while 循環復雜度應該是平方級,但是你這樣想,while 執行的次數就是雙指針 left 和 right 走的總路程,最多是 2M 嘛。
二、找到字符串中所有字母異位詞

這道題的難度是 Easy,但是評論區點贊最多的一條是這樣:
How can this problem be marked as easy?
實際上,這個 Easy 是屬于了解雙指針技巧的人的,只要把上一道題的代碼改中更新結果的代碼稍加修改就成了這道題的解:

因為這道題和上一道的場景類似,也需要 window 中包含串 t 的所有字符,但上一道題要找長度最短的子串,這道題要找長度相同的子串,也就是「字母異位詞」嘛。
三、無重復字符的最長子串

此題難度 Medium,遇到子串問題,首先想到的就是滑動窗口技巧。
類似之前的思路,使用 window 作為計數器記錄窗口中的字符出現次數,然后先向右移動 right,當 window 中出現重復字符時,開始移動 left 縮小窗口,如此往復:

需要注意的是,因為我們要求的是最長子串,所以需要在每次移動 right 增大窗口時更新 res,而不是像之前的題目在移動 left 縮小窗口時更新。
四、模板總結
通過上面三道題,我們可以總結出滑動窗口算法的抽象思想:
int left = 0, right = 0;
while (right < s.size()) {
window.add(s[right]);
right++;
while (valid) {
window.remove(s[left]);
left++;
}
}
其中 window 的數據類型可以視具體情況而定,比如上述題目都使用哈希表充當計數器,當然你也可以用一個數組實現同樣效果,因為我們只處理英文字母。
另外,滑動窗口技巧也可以運用在數組中,比如給一個數組,求其中 sum 最大的子數組,或者求平均數最大的子數組,都可以用滑動窗口技巧解決。
稍微麻煩的地方就是這個 valid 條件,為了實現這個條件的實時更新,我們可能會寫很多代碼。比如前兩道題,看起來解法篇幅那么長,實際上思想還是很簡單,只是大多數代碼都在處理這個問題而已。
-
算法
+關注
關注
23文章
4630瀏覽量
93355 -
滑動窗口法
+關注
關注
0文章
5瀏覽量
2163 -
leetcode
+關注
關注
0文章
20瀏覽量
2342
發布評論請先 登錄
相關推薦
滑動窗口。
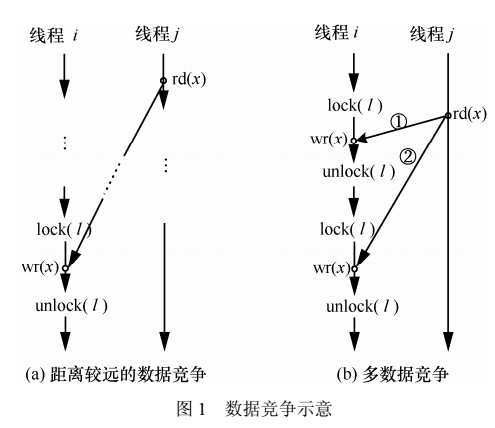
基于滑動窗口的多核程序數據競爭硬件檢測算法
對于絕緣子串,它的電壓分布規律是什么
快慢指針、左右指針的常見算法
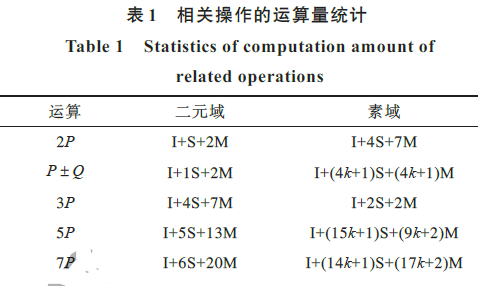
基于MBNS滑動窗口的多標量乘快速算法
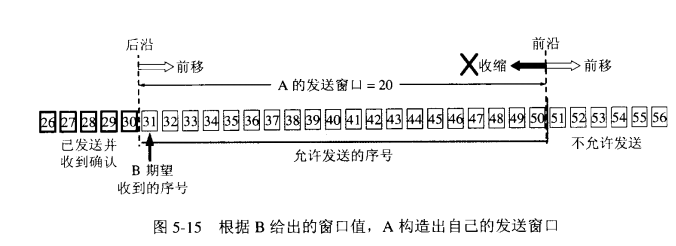
基于滑動窗口的寬度優先搜索算法





 滑動窗口算法解決子串問題教程
滑動窗口算法解決子串問題教程











評論