經常聽到別人提Clark變換，Park變換，FOC和SVPWM，最近研讀了很多非常棒的文章。

終于有點膚淺的認識，本著一邊學一邊筆記的節奏，本文來鞏固下這些知識，也嘗試分享給有需要的不同背景的汽車人。

1 背景

本文采用永磁同步電機來介紹其控制方法，永磁同步電機的結構：轉子為永磁體，定子為三相交流繞組。

一個典型的永磁同步電機的3相繞組在空間120°電角度布置，繞組里面分別通相位相差120°的三相交流電：

為什么需要通相位相差120°的三相交流電？為了產生一個幅值大小不變的圓形旋轉磁動勢。

source: http://www.ece.umn.edu/users/riaz/animations/abcvec.html

針對上圖：設計永磁同步電機，就必須要產生這樣的磁動勢，即通相位相差120°的幅值不變的三相交流電，就會產生一個幅值大小不變的圓形旋轉磁動勢，其大小正好為單相磁動勢最大幅值的1.5倍，如下圖所示。注意觀察上圖！從PhaseA，B，C三圖可以看出，每相電流變化產生的旋轉磁場強弱也在變化，但它們合成旋轉磁場（右下圖Resultant）強弱的不變，其轉速與轉子轉速相同。也可以從空間矢量角度來看它們的變化(右下圖Space vectors)。

從上圖不難發現，如果調節三相交流電幅值，相應地，合成的旋轉磁動勢幅值也隨之變化，當然其大小仍為單相磁動勢最大幅值的1.5倍，見下圖。

source：https://zhuanlan.zhihu.com/p/45757542

磁動勢變化意味著什么呢？電機轉矩的變化，這樣我們需要找到三相交流電與電機轉矩的關系。直接找它們兩者的關系可能比較復雜，在控制實施有難度。那么是否有什么方法可以先做一些處理？注意三相交流電通定子線圈，定子線圈是靜止的，但線圈產生的磁場是與轉子永磁體產生的磁場相互作用，轉子在轉，線圈產生的磁場也在同步轉。通過這些信息，是否能夠找到一些提示？

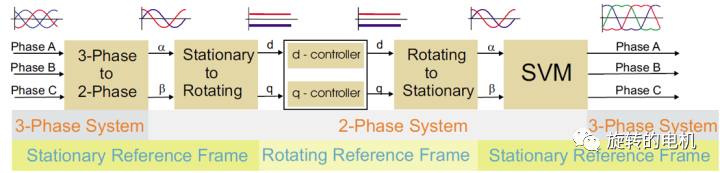
2 Clark和Park變換

對于三相交流電，我們是否可以把它整成兩相？就好比我們看一個三維的問題，我總是傾向于轉化到二維去解決。三相交流電相互間相位相差120°，那我們是否可以構建一個坐標系α-β，使用它來表示三相交流電，如下所示：

也就是把Ia，Ib，Ic投影到該坐標系α-β，不難得到變換公式：

寫成矩陣形式如下：

這就是Clark變換。在上述矩陣前通常會添加系數 2/3或 是sqrt(2/3),分別代表等幅值變換與等功率變換。通過Clark變換，使得原先的三相交流電轉換成兩相正弦電流。

注釋：Clark變換前的三相交流電

注釋：Clark變換后的兩相正弦電流

若此時轉子在轉動，旋轉的轉子永磁體與坐標系α-β有何干系呢？相當于轉子永磁體在坐標系α-β以轉速ω轉動。如果建立一個坐標系d-q，d軸和磁鐵NS線完全重合，并且正方向是N極方向；而q軸，相切于NS線，正方向與轉動方向一致。如下所示：

那么將坐標系α-β投射到這個坐標系d-q，由于轉子相對定子以轉速ω旋轉，即兩個坐標系存在一個旋轉角度θ（θ=ωt）,它們的關系如下所示：

其實從坐標系α-β到坐標系d-q的這個變換就是Park變換。將兩相正弦波信號轉化為兩相的直流信號。

注釋：Park變換后的兩相直流電

上述的坐標系d-q為什么這樣建立? 原因是通過Park變換到Id，Iq，此時d軸方向沒有切割磁感線，所以電流Id并不會產生洛倫茲力；而q軸方向就能切割磁感線，從而電流Iq就能產生洛倫茲力。

以上結合Clark變換和Park變換，就可以將一個三相交流電轉化為兩相的直流電，如下所示：

3 SVPWM

3.1 SVPWM的輸入

對于要如何獲得目標的電磁轉矩，這時只需需要合理地控制Id和Iq。因為根據永磁同步電機的轉矩方程可知：

第1部分是由轉子永磁體磁鏈和三相定子繞組磁鏈相互作用產生的；第2部分是由凸極效應造成磁阻變化而產生的反應轉矩。可以看出，因為轉子永磁體磁鏈恒定不變，要調節永磁同步電機的電磁轉矩，只需要調節Id和Iq。由坐標系d-q的定義，Id沒切割磁感線，Iq切割磁感線，即電磁轉矩與Iq有關，控制Iq就行。

source：TI

令Id=0，根據目標的電磁轉矩就可以確定目標的Iq (Iq=T/pψm )。這樣可以得到電機的總體FOC控制框架：

到此，關鍵是黑盒部分的處理，通常會使用SVPWM來處理，為什么要使用SVPWM? 請參考：如何深入理解SVPWM？- 知乎 (zhihu.com)

SVPWM具體實現是什么功能呢？其實就是將Vα，Vβ轉化為Va，Vb，Vc。下面揭開黑盒部分，如下所示：

source：Mathworks

由上圖可知SVPWM的輸入Vα，Vβ如何獲取：

• 目標的Id，Iq（深藍框）：令目標的Id=0，根據電磁轉矩可得到目標Iq；
• 實際的Id和Iq（綠色路徑）：通過傳感器采集到Ia, Ib, Ic, 經過Clark變換到Iα，Iβ, 再經過Park變換到Id，Iq；
• 有了目標的和實際的Id，Iq，采用PI控制則可以得到目標的Vd，Vq；
• Vd，Vq經反Park變換到Vα，Vβ。

3.2 SVPWM的輸出

那SVPWM的輸出呢？這里需要先了解下逆變器的電路原理，逆變器就是把直流電轉換為交流電，采用3組半橋MOS電路來實現，如下所示：

每組半橋MOS電路由兩個MOS管組成，上橋臂和下橋臂，中間引出一條輸出線。通過控制上下橋臂的通斷，就可以控制輸出，如下所示：

注釋：MOS管看成一個開關就行，其功能就是控制橋臂的通斷

當上橋臂通，下橋臂斷時，輸出OUT接通電源；當上橋臂斷，下橋臂通，輸出OUT接地；當上、下橋臂都通，這個我們在SVPWM不使用。這樣一根輸出線與電機的一根相線相連，使用3組半橋MOS電路就完成了最基本的電機驅動電路。即通過逆變器的3組半橋MOS管電路上下橋臂的通斷控制來實現直流電轉化為三相交流電。

那控制MOS管的通斷，如何就實現了直流電變三相交流電呢？這里需要使用到PWM，PWM定義如下：

source：Mathworks

就是以一定頻率（即上圖的周期T）不斷改變PWM的占空比，比如上圖第一周期T控制占空比20%，能到20V的平均電壓，第2周期T控制占空比50%，能到50V的平均電壓，以此類推，只要頻率夠快，就可以利用PWM控制MOS管的通斷，從而產生近似正弦電流，如下所示：

通過上面的分析可知，通過SVPWM算法得到3組PWM，分別控制3組半橋MOS電路就行。這樣我們就明確了SVPWM的輸入和輸出，接下來我們來了解SWPWM具體是什么

3.3 SVPWM是什么

SVPWM總體邏輯如下示意：

1. 根據反Park變換得到Vα，Vβ，這兩個矢量可以在坐標系α-β合成矢量Vref；
2. 通過控制逆變器的3組半橋MOS電路可以構建6個基本電壓矢量和2個零電壓矢量；
3. 用這8個電壓矢量中的幾個可以合成任意矢量，比如Vref，那意味著可以建立Vα，Vβ和幾個電壓矢量的關系；
4. 8個電壓矢量均與Va，Vb，Vc有關系的，這樣就能夠建立起Vα，Vβ與Va，Vb，Vc的關系。當然如上面SVPWM的輸出所言，Vα，Vβ與Va，Vb，Vc的關系其實通過Vα，Vβ與施加給a, b, c三相電對應的半橋MOS電路的PWM來體現。

接下來就介紹下整個邏輯的實現過程，首先構建電壓矢量。這里以下圖所示的半橋MOS電路狀態來分析，a組的上橋臂通，b, c組的下橋臂通，此時等效電路如下右上圖。通過電路分析可得三相電壓與電源電壓的關系，考慮三相繞組在空間中的分布，將它們表示在一個六等分的圓內，如右下圖，接著矢量合成，不難得到合成的電壓矢量大小（Vdc）和方向(-->A)。

source：Mathworks

接著使用相同方法，分別對不同半橋MOS電路狀態進行分析，可得另外的7個電壓矢量，我們半橋MOS電路的a, b, c上橋臂全通或下橋臂全通構建的2個電壓矢量稱為零矢量，其他6組稱為基本矢量。如下圖所示：

source：Mathworks

同時為了方便快速記憶空間矢量對應的半橋MOS電路狀態，我們采用下面的命名方式：1表示上橋臂通，下橋臂斷；而0表示上橋臂斷，下橋臂通；并且V的下標，由三組半橋MOS電路的狀態（1/0）構建3位二進制數轉化為十進制來表示，比如100表示a組的上橋臂通，下橋臂斷，b,c組的上橋臂斷，下橋臂通，二進制100轉成十進制為4，即V的下標是4，即V4, 以此類推，如下所示：

我們把兩個相鄰基本電壓矢量之間形成的空間稱為扇區，因此有6個扇區。以上就構建好了電壓矢量，接下來就可以利用它們作為基向量來合成任意矢量，那么如何用這些矢量來合成Vref？取決于Vref在哪個扇區。

當然不管Vref在哪個扇區，采用的方法都是選擇該扇區相鄰兩個基本電壓矢量以及零矢量，按照伏秒平衡原則來合成該扇區內的任意電壓矢量，即：

注釋：資料引用出處不統一，本文中V和U等價，均表示電壓，文字均采用V來書寫。

假設V確定了一個PWM周期T內，V4, V6, V0, V7 運行時間，但它們運行的順序呢？，現在的關鍵是一個PWM周期T內，V4, V6, V0, V7分別要運行多長時間?

根據伏秒平衡原則有: Vref = (T4/T)V4+ (T6/T)V6+ (T-T4-T6/T)(V0&V7),如下所示：

將 Uref投影分解到 U4 和 U6 的方向，由正弦定理有：

由此我們可知：T4, T6, T0, T7 的值取決于Vref，Vdc和θ的值，其中Vdc和θ均可通過傳感器實時獲取，可看成是已知量，所以關鍵在Vref，而前面我們提到可以用Vref可以用Vα, Vβ來合成。這樣通過Vref，就是可以建立T4, T6, T0, T7與Vα, Vβ關系，根據如下分析：

可得：

這樣我們可以根據Vα, Vβ（SVPWM的輸入）和 Vdc求得T4, T6, T0, T7。以上我們是以Vref在扇區I為例，為了在其他扇區中重復利用在上述結論并簡化表達式，我們可以定義三個變量：

這樣我們就可以得到每個扇區的時間，如下所示：

這樣就確定了一個PWM周期T內，U4, U6, U0, U7 運行時間，但它們運行的順序呢？理論上任何順序都可以，但是實際中需要考慮更多限制，比如MOS管存在開關損耗，因此希望能盡量減少MOS管的開關次數，那么以這個為目的來設計其順序，如下所示：

注意觀察執行順序的設計，每次只改變一組半橋MOS電路狀態，而且從000開始，結束又回到000，也就是每個PWM周期結束又可以回到初始狀態，絲毫不會影響下一個PWM周期的執行順序。而且通過在合理的位置插入兩個零矢量，對其在時間上進行了平均分配，這樣產生的PWM對稱，可以有效地降低PWM的諧波分量。采用相同的方法，不難得到6個扇區的開關時序，如下所示：

當然上述對于Vref的合成，需要先知道 Vref在哪個扇區，具體怎么判斷？ 不難聯想到高中所學過的線性規劃把V1V6, V3V4, V2V5看成三條直線，用α，β表示這三條直線方程，那么有：

• 直線V3V4: β = 0,
• 直線V2V5: β = -sqrt(3)*α，
• 直線V1V6: β = sqrt(3)*α

為了方便判斷Vref在哪個扇區，由三條直線方程，令

• X = β,
• Y = sqrt(3)*α + β,
• Z = sqrt(3)*α - β,

從而可以將Vref坐標(α，β)代入X, Y, Z，根據X,Y,Z值的正負情況就可以判斷Vref的位置。以Vref在扇區1為例，不難發現，根據X, Z來判斷，顯然X需要大于0，Z也需要大于0，如下所示：

使用相同的方法，可以得到其他扇區的判斷條件：

到此，基本介紹完了SVPWM，內容還是非常多，不過把握好整體邏輯，還是不難理解。如果你已經認真地看到此處，可跳到文章最后看看a, b, c 3組PWM執行是如何實現的。回顧SVPWM整個邏輯：

• 控制3組半橋MOS電路狀態 --> 構建6個基本電壓矢量和2個零矢量；
• 利用基本電壓矢量和零矢量作為基矢量可合成任意矢量，且根據伏秒平衡原則可得到各基矢量的作用時間；
• 根據基矢量（V0~V7)--> Vref <-- Vα，Vβ，可知用Vα，Vβ，Vdc表示各基矢量的作用時間；
• 將幾個基矢量的作用時間合理排序，得到作用于a，b，c 3組半橋MOS電路的占空比（PWM）。

4 總結

上文就介紹完了FOC控制方法的關鍵知識，掌握好了這些知識，那么就能把握FOC控制方法的整體邏輯，讀懂FOC控制方法的代碼或者模型，最后借助下圖在腦海串聯這些知識。

5 彩蛋

基于SVPWM排序之后得到PWM波形，有個問題：從000到100，怎么判斷執行切換？從圖看是過了T0/2時間就執行，但是怎么知道的？其原理是怎樣的？

接下來我們就要解釋這個問題，首先定義三個時間變量Ta，Tb，Tc：

將這三個時間變量與一個三角波比較后算法就能精確的在指定的時間進行切換，但是這個三角波需要是一個等腰直角三角形，即高是底邊的一半，高代表半個PWM周期，即Ts/2。自然地，底就是1個PWM周期，即Ts。

接下來結合下圖理解下這三個時間變量與一個三角波比較實現切換的原理。

• 當三角波發生器開始產生，經過t=T0/2時間，即Ta，下一刻意味著t>Ta，那么在t=Ta時刻開始從000切換到100，即a組半橋MOS管從上橋臂斷，下橋臂通切換到上橋臂通，下橋臂斷。
• 隨著時間t=Tb，下一刻意味著t>Tb，那么在t=Tb時刻開始從100切換到110，即b組半橋MOS管從上橋臂斷，下橋臂通切換到上橋臂通，下橋臂斷。
• 以此邏輯，在t=Tc時刻開始從110切換到111，即c組半橋MOS管從上橋臂斷，下橋臂通切換到上橋臂通，下橋臂斷。
• 最終經過t=Ts/2時間，三角波到達其頂點。

當三角波到達其頂點，接下來從頂點減小到0。不難理解，將會在t=Ts-Tc，從111切換到110；lt=Ts-Tb，從110切換到100；t=Ts-Ta，從100切換到100，所以通過整個過程的比較分析，就可明白三個時間變量與一個三角波比較實現切換的原理，如下所示：

本文到此結束，預告下篇文章將結合電機map介紹完整的電機控制方法。