01 導讀
1.1 基于高非線性光纖中前向布里淵散射的聲阻抗傳感技術
基于布里淵散射的光纖傳感系統能進行長距離、分布式地測量。然而在基于后向布里淵散射的分布式光纖傳感系統中,光場和縱向聲波均被束縛在纖芯中傳播,因此可以測量的物理量也局限于溫度、應變以及振動等,而無法對光纖外部的物質進行探測。另一方面,光纖中除了后向布里淵散射外,光纖中還存在前向布里淵散射。利用前向布里淵散射(FBS)中的橫向聲波可以對光纖外界物質的聲阻抗進行測量,進而實現光纖外部物質探測。然而標準單模光纖(SSMF)中前向布里淵散射的增益較小,使得信號信噪比較差,導致基于SSMF的聲阻抗傳感靈敏度較低,難以實現高靈敏度的外界物質探測。
針對上述問題,華中科技大學唐明教授、王亮教授團隊提出了一種基于高非線性光纖(HNLF)中前向布里淵散射的高靈敏度聲阻抗測量技術。通過仿真證明了HNLF中徑向聲模式(R0,m)引起的FBS相比于SSMF中的FBS具有更高的增益系數和散射效率,這為聲阻抗測量提供了更好的信噪比及更高的傳感靈敏度。實驗中測得HNLF中模式的聲阻抗靈敏度為3.83MHz/[kg/(s·mm2)],比SSMF中增益幾乎最大的R0,9模式的2.70MHz/[kg/(s·mm2)]高了1.42倍。同樣對HNLF中TR2,5模式進行聲阻抗測量,其靈敏度為0.24MHz/[kg/(s·mm2)],比SSMF中相同模式的靈敏度高了1.5倍。研究成果以“High-sensitivity acoustic impedance sensing based on forward Brillouin scattering in a highly nonlinear fiber”為題發表在Optics Express期刊上。華中科技大學碩士研究生曾柯諺為論文第一作者,王亮教授為論文通訊作者。
1.2 基于高非線性光纖中前向布里淵散射的溫度和應變同時傳感
布里淵光纖傳感器因其出色的溫度和應變傳感能力而引起了廣泛的研究興趣。不過布里淵光纖傳感器大多是基于后向布里淵散射(BBS),其中布里淵頻移(BFS)與溫度和應變均線性相關。然而,BFS存在溫度和應變的交叉敏感性,使得溫度和應變的同時測量變得困難。目前已經提出了多種解決方案來實現雙參量同時測量,其中使用具有多峰布里淵增益譜(BGS)的光纖可以算作溫度及應變同時測量中最有效且簡單的方法之一。然而,由于BBS的BFS通常在~10GHz左右,因此需要頻率范圍達到~10GHz的微波源進行測量,這使得實驗裝置的成本增高。此外,由于BGS的線寬相對較寬(幾十MHz),在提取BGS的BFS時,不僅需要更多的頻率掃描次數,而且測量誤差也相對較大。
針對上述問題,華中科技大學唐明教授、王亮教授團隊提出了一種基于高非線性光纖(HNLF)中前向布里淵散射(FBS)的增強型溫度及應力同時傳感技術。方案利用HNLF中的FBS首次實現了溫度和應變同時傳感。原理是利用了徑向聲模式R0,m和扭轉-徑向聲模式TR2,m對于溫度和應變的不同響應。為了提高測量靈敏度,我們選擇了在HNLF中具有較大FBS增益的高階聲模式用于測量。進一步地,為了減小測量誤差,我們提出了一種選擇最佳模式組合的方法,該組合具有最小測量誤差,并通過仿真和實驗進行了驗證。工作中選擇了三種模式組合進行溫度和應力的同時測量,通過模式組合選擇方法,通過(R0,18, TR2,29)實現了最低的溫度和應變誤差0.12°C/39με。與基于BBS的傳感器相比,該方案只需要測量1GHz左右的頻率,不需要~10GHz的微波源,有效降低了系統成本。此外,FBS的諧振頻率和譜線寬度都比BBS小得多,也有效提高了測量精度。研究成果以“Simultaneous Sensing of Temperature and Strain with Enhanced Performance using Forward Brillouin Scattering in Highly Nonlinear Fiber”為題發表在Optics Letters期刊上。華中科技大學博士研究生楊貴江為論文第一作者,王亮教授為論文通訊作者。
02 研究背景
2.1 基于高非線性光纖中前向布里淵散射的聲阻抗傳感技術
近年來,FBS技術的應用使其能夠根據測量的聲阻抗來識別光纖外物質的環境檢測。由于橫波的參與,基于FBS的傳感器可以測量光纖外物質的聲阻抗,而不需要特殊的結構,使用普通光纖即可完成。但是標準單模光纖(SSMF)中FBS增益較弱,聲阻抗傳感的靈敏度較低。
為解決上述問題,本團隊提出基于HNLF中FBS進行聲阻抗傳感,首次演示了靈敏度超過3MHz的聲阻抗傳感。得益于高聲光耦合效率,HNLF中R0,m和TR2,m誘導的FBS都比SSMF具有更大的增益系數和散射效率。這提供了更好的信噪比(SNR),因此更大的測量靈敏度。通過在HNLF中使用R0,20模式,我們獲得了3.83MHz/[kg/(s·mm2)]的更高靈敏度,而在SSMF中使用R0,9模式(幾乎具有最大的增益系數)測量時的靈敏度為2.70MHz/[kg/(s·mm2)]。同時,在HNLF中使用TR2,5模式時,測量到的靈敏度為0.24MHz/[kg/(s·mm2)],仍然是在SSMF中使用相同模式時的1.5倍。靈敏度的提高將使基于FBS的傳感器對外部環境的檢測更加準確。
2.2 基于高非線性光纖中前向布里淵散射的溫度和應變同時傳感
對于基于BBS的溫度及應變傳感器,由于需要頻率范圍達到~10GHz的微波源進行測量,使得系統成本很高。并且線寬較寬(幾十MHz)的BGS也使得頻率掃描過程耗時較長,且從BGS中提取BFS時也會產生較大的測量誤差。另一方面,對于前向布里淵散射(FBS),它是由入射光場與光纖中橫聲波場相互作用而產生的,通常其共振頻率在幾十MHz到1GHz左右,譜線線寬為幾MHz,都比BBS小得多。因此,使用基于FBS的傳感器進行溫度和應變傳感不僅可以降低測量成本,而且還可以提高傳感精度。但FBS中仍存在溫度與應變的交叉敏感性。最近,L.A.SáNCHEZ等人在長周期光柵中使用FBS來區分溫度和應變。但是,這種光柵需要改變光纖結構,不適合分布式傳感。
為解決上述問題,本團隊首次提出并展示了使用HNLF中的FBS效應來實現溫度和應變的同時測量,其較大的高頻增益增強了傳感性能。并且我們提出了一個理論誤差模型,幫助選擇最佳的模式組合,實現最小的測量誤差。實驗中采用三種模式組合進行展示,其中基于模式組合(R0,18, TR2,29 )獲得了最低溫度和應變誤差0.12℃和39με。與基于BBS的傳感器相比,該方法只需要在~1 GHz范圍內進行測量,可以用更便宜的設備實現高精度測量。此外,FBS增益譜的窄線寬也提高了傳感精度。
03 創新研究
3.1 基于高非線性光纖中前向布里淵散射的聲阻抗傳感技術
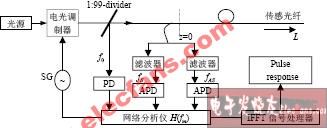
本工作使用了基于光纖薩格納克環的實驗裝置,用于測量FBS頻譜并演示基于HNLF的高靈敏度聲阻抗傳感,如圖1所示。激光器輸出波長為1550.12 nm的入射光,經過光纖隔離器后被摻鉺光纖放大器放大光功率,隨后經過一個光纖濾波器用于濾除摻鉺光纖放大器引起的自發輻射噪聲,之后進入薩格納克環中。其中,薩格納克環包括一個50:50光纖耦合器,一個偏振控制器以及待測光纖。在待測光纖內,泵浦光將激勵橫向聲波,并通過調整環內的偏振控制器,可以激勵或者抑制R0,m模式和TR2,m模式,同時也可以將聲學模式引起的相位調制轉換為強度調制,最終和反向傳播的光在耦合器處干涉輸出。拍頻信號由1.5 GHz的探測器接收,并在電頻譜分析儀上顯示前向布里淵散射的頻譜信號。
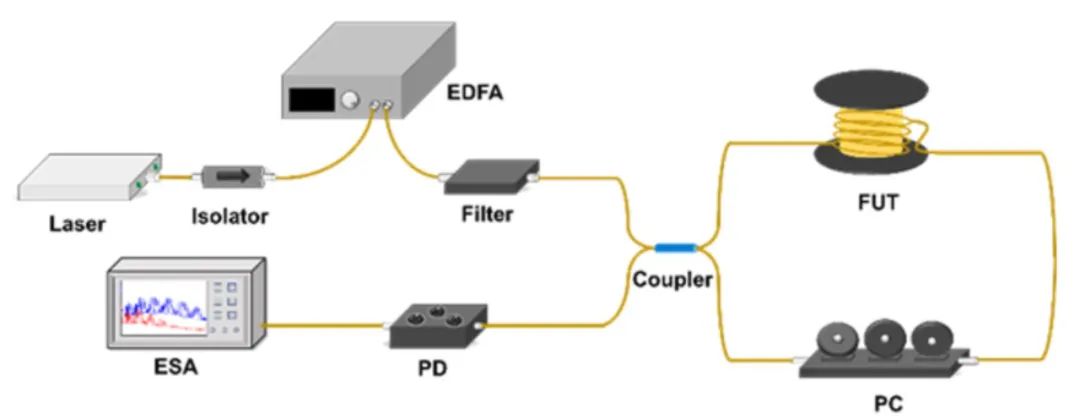
圖1 利用FBS測量光纖外界聲阻抗的實驗裝置圖
圖源: Optics Express (2023)。
https://doi.org/10.1364/OE.483085 (Fig. 5)
實驗中使用的HNLF的纖芯直徑為4.45,包層直徑為127,模場直徑為3.3且HNLF的光纖損耗小于1.5 dB/km。圖3(a)和(b)分別展示了940 m長的HNLF (藍色)中R0,m模式和TR2,m模式1.5 GHz范圍內的FBS增益譜。作為對比,同樣測量了1 km的SSMF(紅色)中對應的FBS增益譜。為了比較公平,對EDFA的輸出功率進行調整,以保證通過SSMF后的光功率與通過HNLF后的光功率一致。如圖2(a)所示,由于HNLF較高的增益系數,當共振頻率超過1.2 GHz時,其R0,m模式的共振峰值仍然很高。相反地,當共振頻率超過800 MHz時,圖2(a)中SSMF的共振峰就幾乎消失。同樣對于TR2,m模式來說,HNLF在較寬的頻率范圍內都有更強的共振峰值,而SSMF中共振峰在超過500 MHz的范圍外就幾乎消失了。如果將圖2(a)中HNLF和SSMF測得的結果基線設置為同一水平線,將發現HNLF的最大功率比SSMF中大3 dB以上。不同的基線是由于HNLF和SSMF使用了不同的泵浦光功率來補償光纖的損耗,以便進行公平的比較。
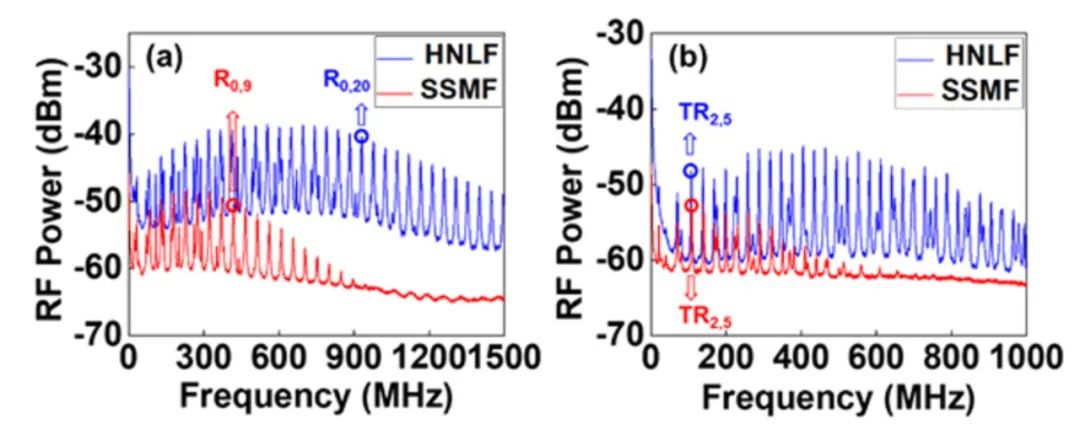
圖2 HNLF(藍色)和SSMF(紅色)中:(a) R0,m模式和(b) TR0,2m模式對應的FBS增益譜
圖源: Optics Express (2023)。
https://doi.org/10.1364/OE.483085 (Fig. 6)
對于聲阻抗傳感實驗,由于光纖的丙烯酸酯涂覆層的損耗較高,會對測量結果造成影響,因此在實驗中,選取了一段10m去除涂覆層的HNLF作為待測光纖,并將光纖置于0%~40%濃度的蔗糖溶液中(0%濃度對應純水)。注意到,當蔗糖溶液的濃度低于50%時,其溶液濃度與溶液的聲阻抗呈現線性關系。選擇了R0,20模式對應的FBS增益譜進行聲阻抗的測量,因其能避免其余TR2,m模式的串擾,并且其幾乎為增益最大的模式。將HNLF置于不同外界物質中測量得到的FBS增益譜如圖3所示。圖3(a)展示了去除涂覆層的HNLF置于空氣中的FBS增益譜,并作為參考,R0,20模式峰值旁的小峰是由TR2,49模式的不完全抑制引起的。通過對測得的FBS增益譜進行洛倫茲曲線擬合,可以得到不同環境下的FBS增益譜線寬,當HNLF置于空氣中時,其線寬為1.60 MHz。測量的線寬的值比仿真中的值稍大,可能是光纖包層的不均勻性所導致。純水時,圖3(b)對應的FBS增益譜的線寬為4.76 MHz。對比空氣中測量的結果,光纖置于純水中會導致線寬顯著變寬,且由于外界物質的聲阻抗的變化,光纖包層和外界物質邊界處的聲反射率也隨之變化,聲波反射能量減小,信號強度降低。圖3(c)-(f)分別展示了溶液濃度為10% ~ 40%(10%濃度間隔)時測量的FBS增益譜,且擬合后計算出對應的線寬分別為5.01 MHz、5.76 MHz、6.05 MHz和6.66 MHz。可以看到,隨著蔗糖溶液的增加,增益譜的線寬也隨之增加R0,20模式的共振頻率為930.7 MHz。圖3(g)繪制了不同濃度的蔗糖溶液的聲阻抗與測量的線寬的關系。通過線性擬合,HNLF中R0,20模式的聲阻抗靈敏度為3.83±0.19MHz/[kg/(s·mm2)]。我們也利用了HNLF中的其他聲學模式進行了聲阻抗傳感實驗,結果如圖4(a)-(c)所示。當使用HNLF中R0,19、R0,20和R0,21模式時,對應的靈敏度分別為3.70±0.15MHz/[kg/(s·mm2)]、3.73±0.21MHz/[kg/(s·mm2)]和3.68±0.22MHz/[kg/(s·mm2)]。可以看到相鄰模式的聲阻抗靈敏度有微小的差異。
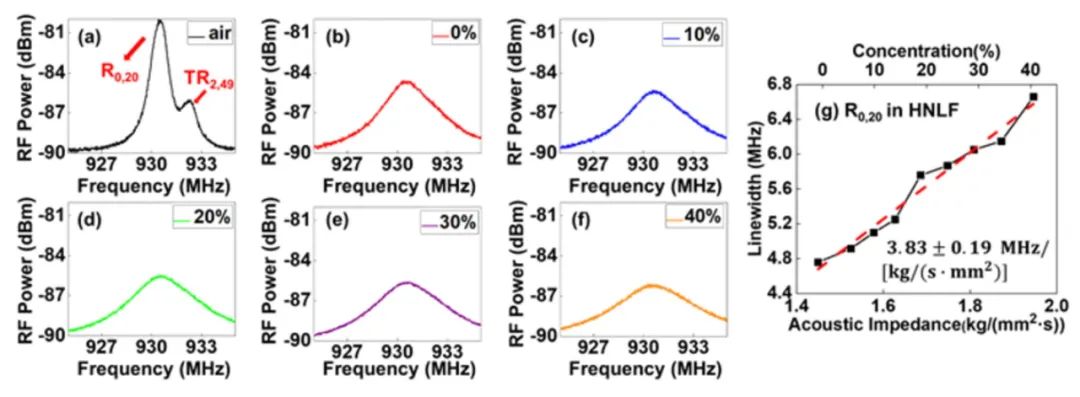
圖3 利用HNLF在不同外界物質情況下測量的R0,20模式增益譜:(a) 空氣;(b) 0%;(c) 10%;(d) 20%;(e) 30%;(f) 40% 濃度的蔗糖溶液;(g) FBS線寬隨聲阻抗的變化關系
圖源: Optics Express (2023)。
https://doi.org/10.1364/OE.483085 (Fig. 7)
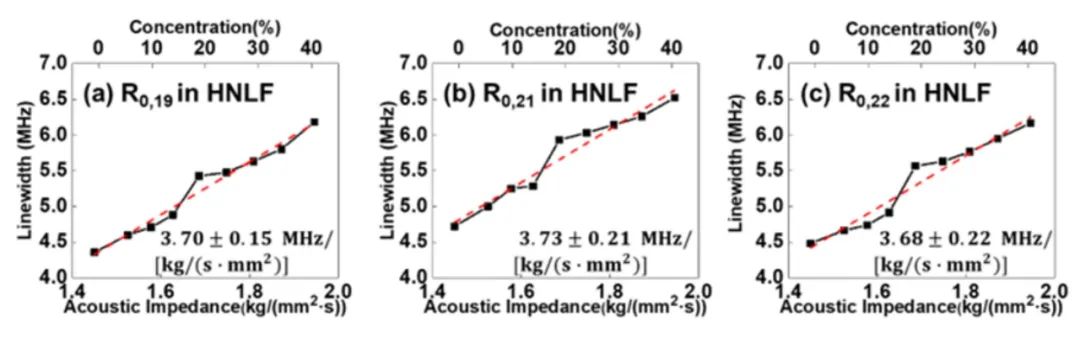
圖4 利用HNLF中不同聲模式測得的FBS增益譜線寬隨聲阻抗的變化:(a) R0,19;(b) R0,21;(c) R0,22
圖源: Optics Express (2023)。
https://doi.org/10.1364/OE.483085 (Fig. 8)
作為對比,將一段去除涂覆層的10m SSMF作為待測光纖進行相同的聲阻抗傳感測量。測量過程中,選取了增益幾乎最大的R0,9聲模式對應的FBS增益譜。不同環境下的FBS增益譜如圖5(a)-(f)所示,其中圖5(a)對應SSMF置于空氣中的結果,計算出對應的線寬為0.60 MHz,圖5(b)-(f)分別對應0% ~ 40%濃度的蔗糖溶液,擬合后的線寬分別為4.03 MHz、4.40 MHz、4.74 MHz、5.00 MHz和5.43 MHz。R0,9模式的共振頻率為417.8 MHz。通過線性擬合,SSMF中R0,9模式的聲阻抗靈敏度為2.70±0.13MHz/[kg/(s·mm2)],如圖5(g)所示。同樣對SSMF中R0,7和R0,8模式進行了相同的測量,這兩個聲學模式對應的聲阻抗靈敏度分別為2.46±0.13MHz/[kg/(s·mm2)]和2.21±0.12MHz/[kg/(s·mm2)],如圖6(a)和(b)所示。由于在SSMF中,R0,5模式和TR2,21/TR2,22模式之間的頻譜有很大的重疊,因此沒有選取R0,5模式進行傳感實驗。通過對比圖3-4以及圖5-6,相比于SSMF,利用HNLF可以實現超過3MHz/[kg/(s·mm2)]的聲阻抗靈敏度。
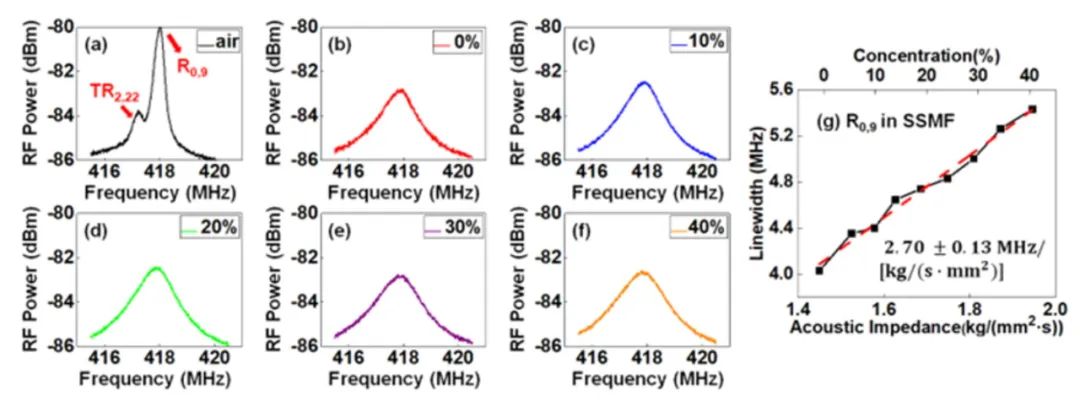
圖5 利用SSMF在不同外界物質情況下測量的R0,9模式增益譜:(a) 空氣;(b) 0%;(c) 10%;(d) 20%;(e) 30%;(f) 40% 濃度的蔗糖溶液;(g) FBS線寬隨聲阻抗的變化關系
圖源: Optics Express (2023)。
https://doi.org/10.1364/OE.483085 (Fig. 9)
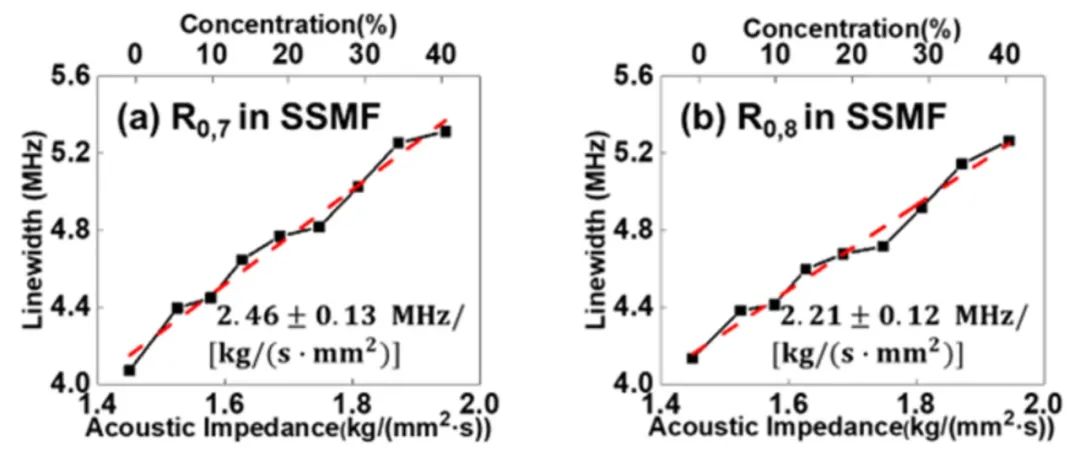
圖6 利用SSMF中不同聲模式測得的FBS增益譜線寬隨聲阻抗的變化:(a) R0,7;(b) R0,8
圖源: Optics Express (2023)。
https://doi.org/10.1364/OE.483085 (Fig. 10)
最后我們也利用HNLF中TR2,m模式進行了聲阻抗傳感實驗。實驗中選擇了TR2,5聲模式(共振頻率為106.9 MHz)進行聲阻抗的測量。TR2,5模式可以避免R0,m模式的串擾,且散射效率為0.51,仍然保持較好的水平。實驗結果如圖7所示。圖7(a)展示了HNLF置于空氣中的結果,且擬合得到的線寬為0.13 MHz。圖7(b)-(f)展示了不同濃度的蔗糖溶液中測量得到的FBS增益譜,擬合得到的線寬分別為0.23 MHz、0.25 MHz、0.27 MHz、0.30 MHz和0.35 MHz。通過線性擬合可以得到線寬隨聲阻抗的變化,且HNLF中模式的聲阻抗靈敏度為0.24±0.1MHz/[kg/(s·mm2)],如圖7(g)所示。而SSMF中相同聲模式的靈敏度為0.16MHz/[kg/(s·mm2)] [51],因此利用HNLF可以將TR2,m模式聲阻抗的靈敏度提高1.5倍。
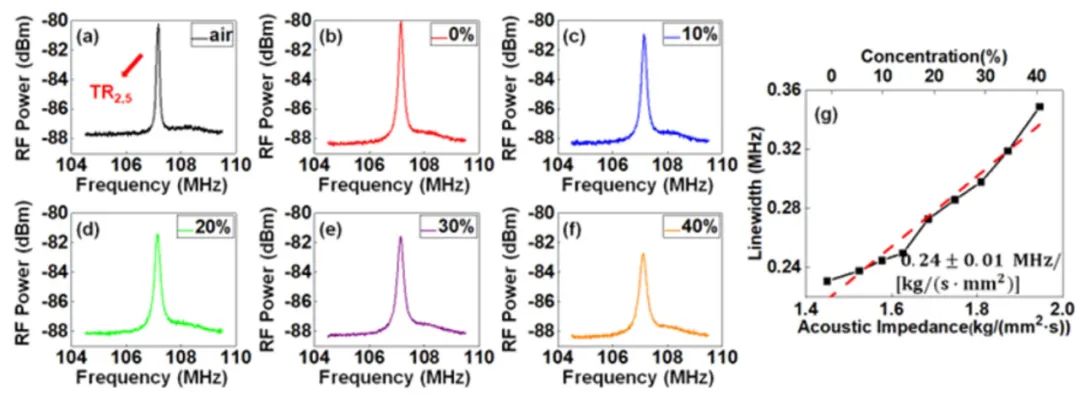
圖7 利用HNLF在不同外界物質情況下測量的TR2,5模式增益譜:(a) 空氣;(b) 0%;(c) 10%;(d) 20%;(e) 30%;(f) 40% 濃度的蔗糖溶液;(g) FBS線寬隨聲阻抗的變化關系
圖源: Optics Express (2023)。
https://doi.org/10.1364/OE.483085 (Fig. 11)
3.2 基于高非線性光纖中前向布里淵散射的溫度和應變同時傳感
光纖內FBS的橫向聲模可分為R0,m和TR2,m兩類模式。對于高階聲場模式,其共振頻率與溫度和應力呈現線性相關,其中R0,m和縱波聲速VL線性相關,TR2,m則與橫波聲速VS線性相關。因此,R0,m和TR2,m的共振頻率將對溫度和應力具有不同的線性響應。本工作即是通過兩者的不同響應系數(1)構建方程組以同時求解溫度和應力,表達式如下:
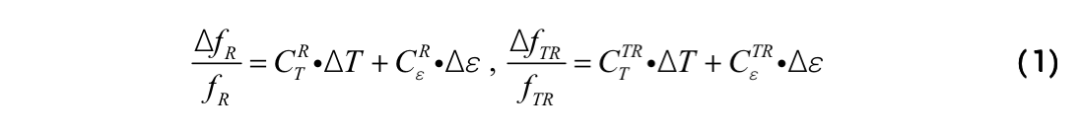
其中,fR和fTR是光纖處于室溫且零應力下的諧振頻率,作為參考頻率;CR T(CTR T)和CR ε(CTR ε)是R0,m(TR2,m)的相對溫度系數和應變系數。此時溫度和應力的測量誤差則可以表示為:
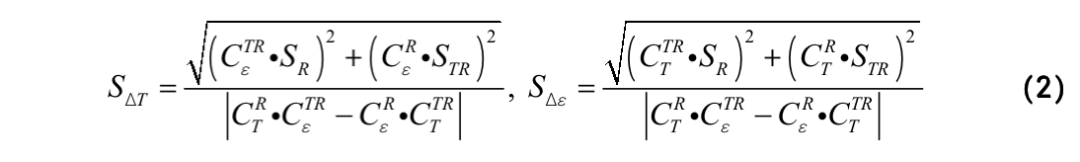
其中,SR 和STR分別表示ΔfR/fR 和ΔfTR/fTR的標準差。并且由于FBS增益譜為洛倫茲型,因此SR 和STR可以進一步寫為:
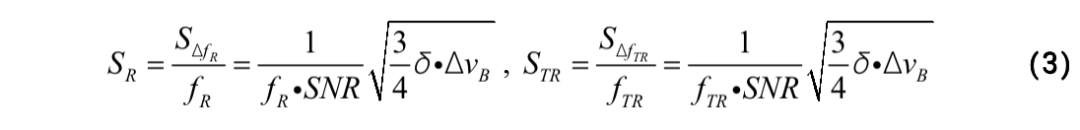
其中,SNR, δ和ΔνB分別表示FBS頻譜的信噪比,頻率間隔以及線寬。從式(2)和(3)可以得到,高共振頻率、高信噪比和窄線寬是實現低測量誤差的理想條件。但高共振頻率的FBS頻譜由于增益小,信噪比通常較低,特別是在標準單模光纖中,高共振頻率下的FBS增益幾乎為零。因此,單純采用高頻聲學模式并不能保證測量誤差最小,需要在信噪比和共振頻率之間進行權衡。
由于不同聲模對溫度和應變的響應不同,所以不同的模式組合會產生不同的測量誤差。為了選擇最佳的模式組合以實現最小的測量誤差,本工作分析了HNLF中聲學模式的前向布里淵散射效率。圖8顯示了我們的HNLF在0-1.5GHz頻率范圍內R0,m和TR2,m模式的歸一化散射效率。可以看到,在HNLF中,即使在1GHz以上的高頻下,R0,m和TR2,m仍然具有較高的散射效率,在更寬的頻率范圍內獲得更大的FBS增益。但是當頻率變高時,散射效率仍會降低,從而降低了SNR。基于散射效率和式(2)和(3)可以分析不同模式組合下的理論溫度和應變誤差,如圖9所示。
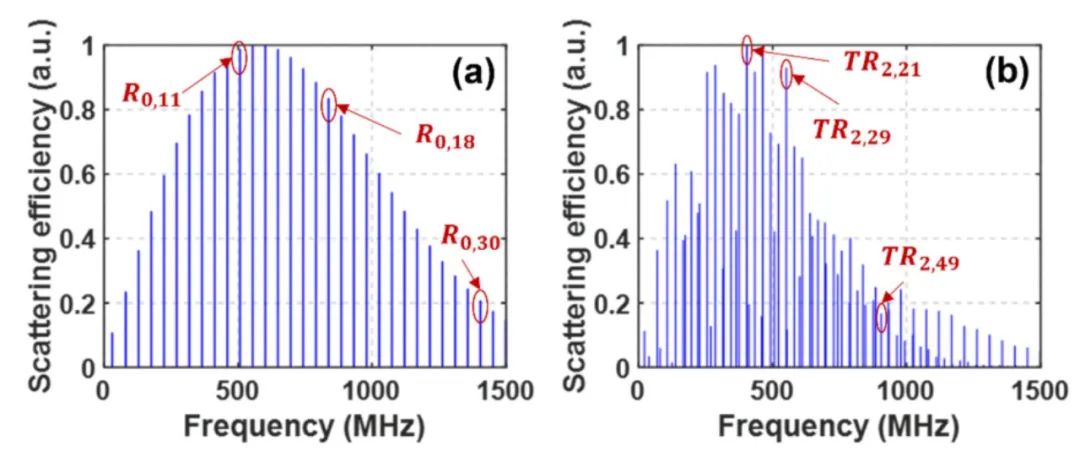
圖8 (a) R0,m和 (b) TR2,m模式的歸一化散射效率
圖源: Optics Letters (2023)。
https://doi.org/10.1364/OL.493637 (Fig. 1)
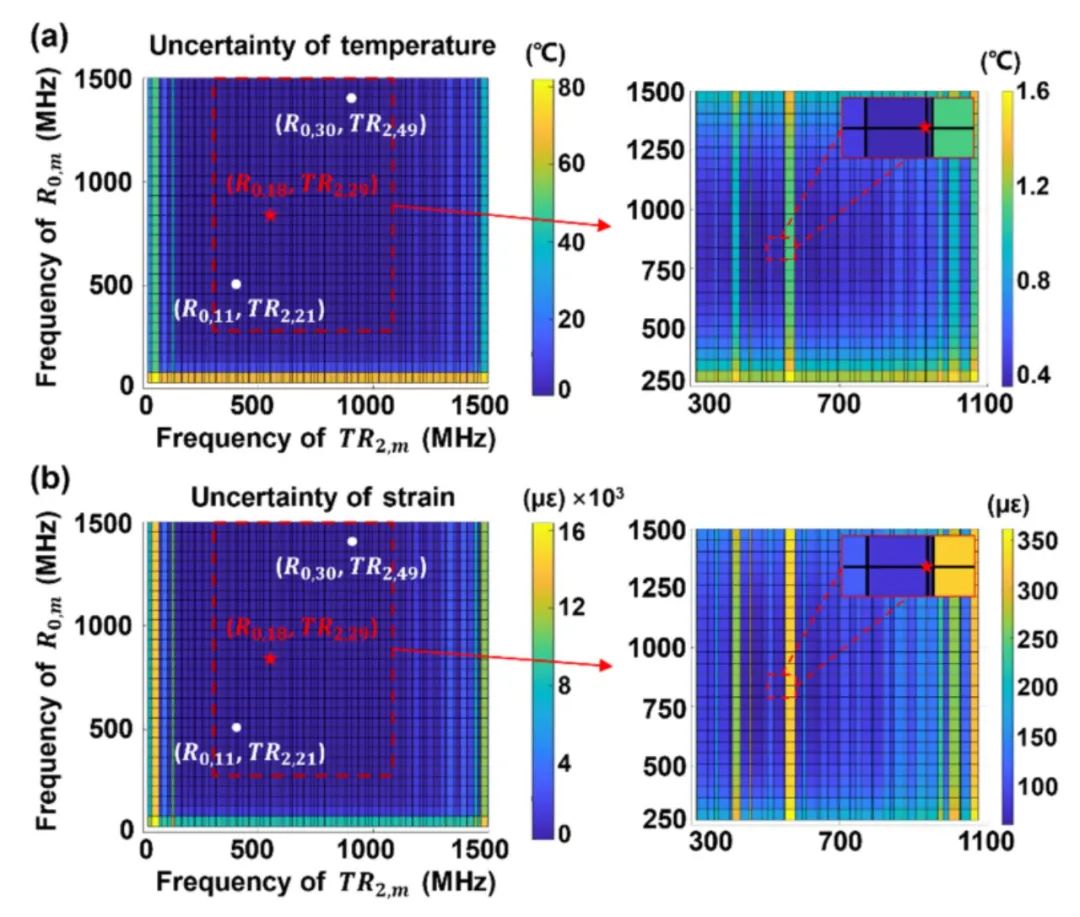
圖9 不同模式組合的理論(a)溫度和(b)應變誤差。插圖:虛線區域的放大視圖
圖源: Optics Letters (2023)。
https://doi.org/10.1364/OL.493637 (Fig. 2)
可以看出不同的模式組合會產生不同的測量誤差,使用頻率過高或過低的聲學模式都會產生較大的誤差。從圖9中可以選出具有最小誤差的模式組合(R0,18, TR2,29),理論誤差為0.35°C/59.98με。此外,還選擇了(R0,11, TR2,21)和(R0,30, TR2,49)兩種典型模式組合進行對比展示,其中前者具有高信噪比(理論溫度/應變誤差為0.48°C/80.33με),后者具有高共振頻率(理論溫度/應變誤差為0.9°C/174.22με)。可見,同時使用高頻聲模或使用高信噪比都不能保證最佳精度,需要權衡信噪比和共振頻率。
本工作使用了基于光纖薩格納克環的實驗裝置,用于測量FBS頻譜并展示基于HNLF中FBS的溫度和應力同時傳感。我們通過調整不同的溫度和應力測量了六個模式在不同情況下的FBS譜。以圖10為例,分別展示了R0,18和TR2,29模式在不同溫度和應變下的頻譜。之后繪制不同聲模的共振頻率與溫度/應變的關系,如圖11所示。我們可以看到R0,m和 TR2,m模式的共振頻率與溫度和應變呈線性關系,不同模式對溫度和應變的靈敏度不同。我們計算了各個模式的溫度及應力系數并在圖11中進行了標注。
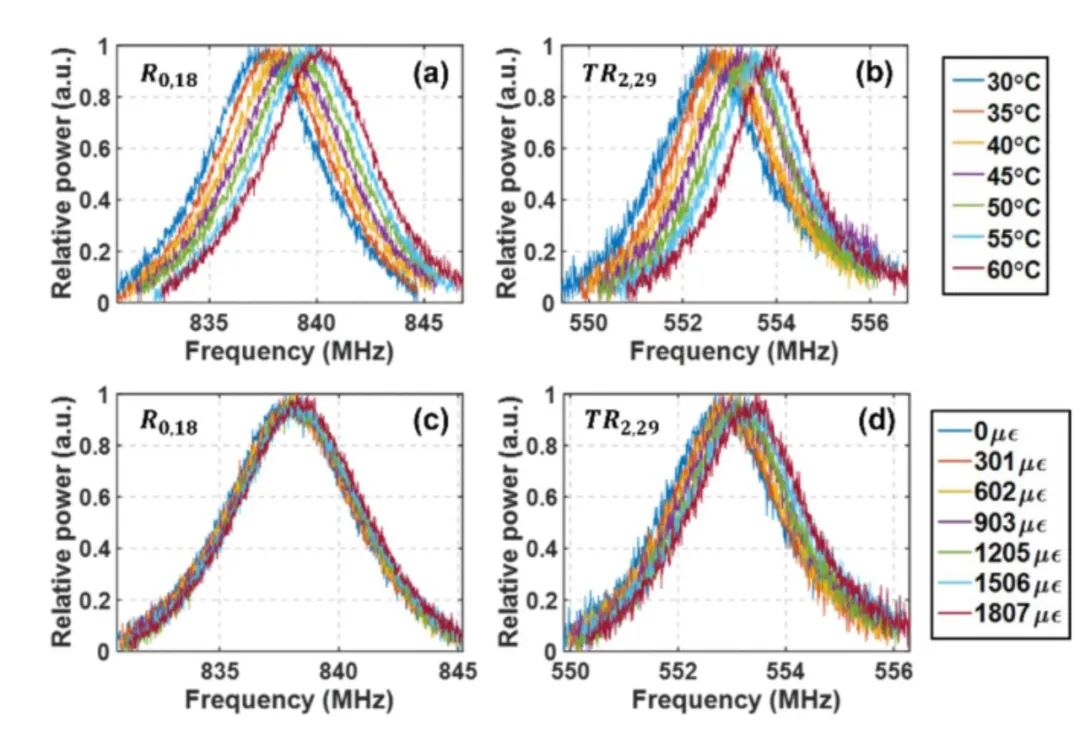
圖10 (a, c) R0,18和(b, d) TR2,29在不同溫度和應變值下的FBS頻譜
圖源: Optics Letters (2023)。
https://doi.org/10.1364/OL.493637 (Fig. 4)
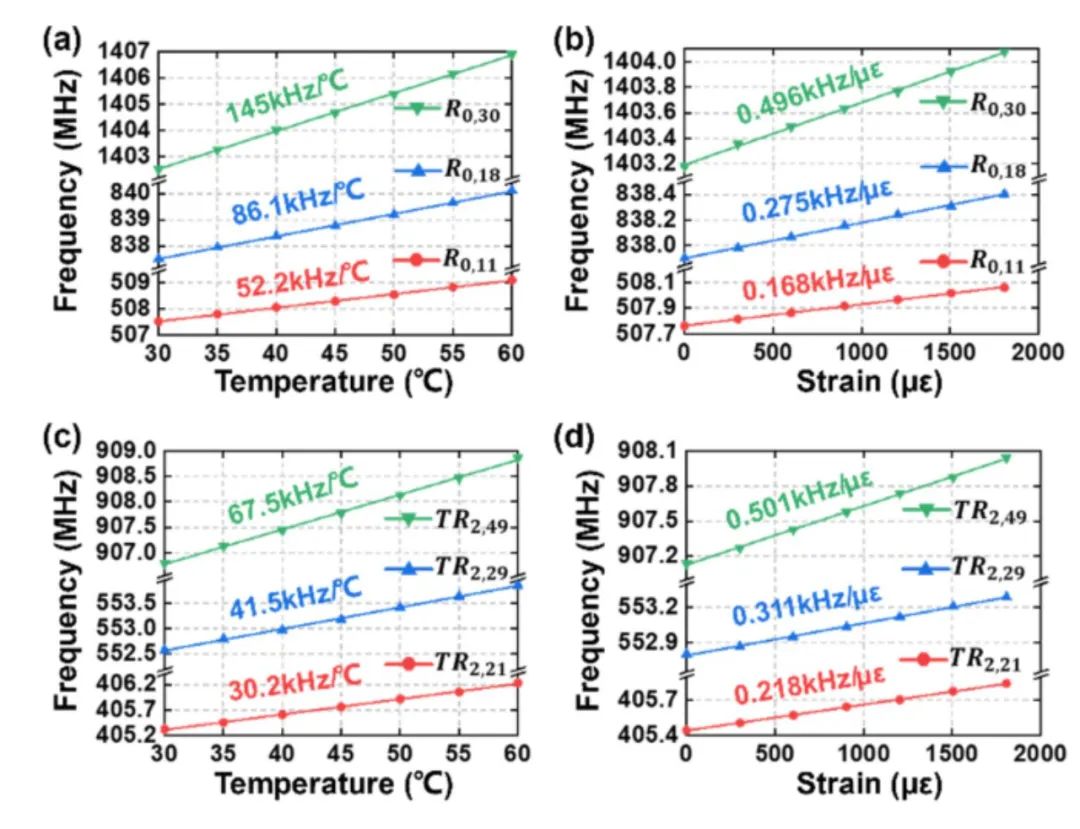
圖11 (a, b) R0,11、R0,18和R0,30的共振頻率與溫度/應變的關系;
(c, d) TR2,21、TR2,29和TR2,49的共振頻率與溫度/應變的關系
圖源: Optics Letters (2023)。
https://doi.org/10.1364/OL.493637 (Fig. 5)
最后在實驗中設定三個具有不同溫度和應力的狀態,成功驗證了該傳感方法的有效性。結果如表1所示,表中給出了不同模式組合下的溫度/應變測量誤差(以標準差表示,標準差是通過重復測量10次獲得的)。通過表1,可以得到使用(R0,18, TR2,29)的模態組合可以獲得0.12°C/39με的最低溫度/應變誤差,平均誤差也僅為0.14°C/42.29με。而使用另外兩個模式組合所產生的測量誤差則更大。實驗結果再次證實,雖然(R0,11, TR2,21)模式具有高信噪比,但由于其相對較低的共振頻率(或靈敏度),它們不能提供最佳精度。同樣,(R0,30, TR2,49)模式組合雖然共振頻率較高,但由于信噪比較低,仍然無法達到最佳精度。
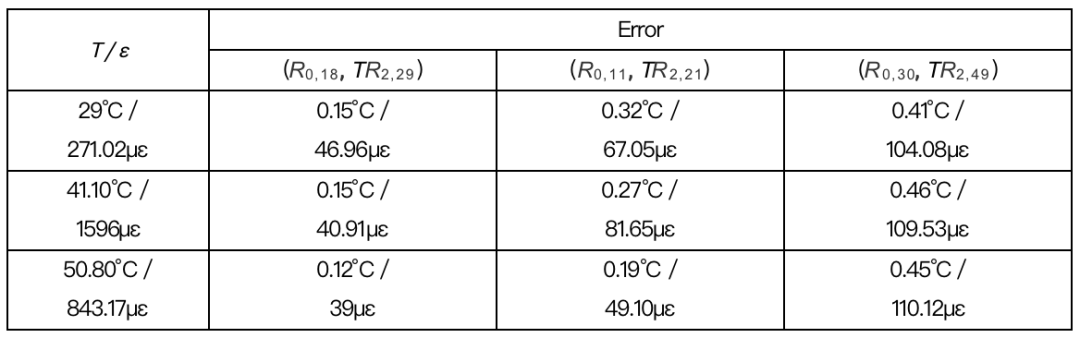
表 1實驗測量誤差
表源: Optics Letters (2023)。
https://doi.org/10.1364/OL.493637 (Table 3)
04 應用與展望
本團隊提出了基于HNLF前向布里淵散射的高靈敏度聲阻抗傳感技術。利用HNLF中R0,m模式引起的前向布里淵散射,首次展示了超過3MHz/[kg/(s·mm2)]靈敏度的聲阻抗傳感。通過仿真分析,證明了HNLF中高階聲場模式的振動更密集且強度更集中在纖芯部位,因此相比于SSMF,HNLF具有更高的聲光耦合效率及增益,從理論上展示了利用HNLF進行高靈敏度聲阻抗傳感的可行性。通過實驗測量了HNLF和SSMF中的FBS增益譜,并利用其進行了聲阻抗傳感。結果表明,HNLF中R0,20模式的聲阻抗靈敏度達到了3.83MHz/[kg/(s·mm2)],而SSMF中增益幾乎最大的R0,9模式的靈敏度僅為2.70MHz/[kg/(s·mm2)],利用HNLF將聲阻抗靈敏度提高了1.42倍。另外,本文也利用了HNLF中TR2,5模式進行聲阻抗傳感實驗,測得其傳感靈敏度為0.24MHz/[kg/(s·mm2)],該數值比SSMF中相同的TR2,5模式的靈敏度高了1.5倍。
此外,本團隊還成功地演示了基于HNLF中FBS的增強型溫度和應變同時傳感。通過使用具有較大FBS增益的高階聲模,提高了測量靈敏度和精度。之后為了解決信噪比和共振頻率之間的權衡問題,提出了一種選擇最佳模式組合以實現最小誤差的方法,并通過仿真和實驗進行了驗證。當在HNLF中使用(R0,18, TR2,29)模式時,溫度和應變誤差最低為0.12°C/39με。與基于BBS的傳感器相比,該傳感器只需要低頻測量,不需要~10GHz的微波源,實現了較低的成本。同時,由于FBS頻譜的共振頻率和線寬較小,也進一步提高了測量精度。此外,如果結合時域分析技術,該方案也可以以分布式方式運行。相信基于FBS的傳感方案將有潛力成為同時監測溫度和應變的高精度且低成本的候選方案。
-
光纖傳感器
+關注
關注
16文章
318瀏覽量
34836 -
光纖
+關注
關注
19文章
3951瀏覽量
73613 -
傳感技術
+關注
關注
4文章
532瀏覽量
46394
原文標題:OE&OL:基于高非線性光纖中前向布里淵散射的增強型聲阻抗傳感以及溫度和應變同時傳感技術
文章出處:【微信號:光纖傳感Focus,微信公眾號:光纖傳感Focus】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 基于高非線性光纖中前向布里淵散射的增強型聲阻抗傳感以及溫度和應變同時傳感技術
基于高非線性光纖中前向布里淵散射的增強型聲阻抗傳感以及溫度和應變同時傳感技術


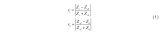










評論