增益裕量GM>0,相位裕量PM>0
為何存在嚴重的使用局限,甚至直接失效。
典型奈奎斯特圖→波特圖穩定裕量
為了便于觀察波特圖的穩定裕量,以常見的:
- 0型(分母不含s),ω從0°出發(Re正軸),回到-270°(Im正軸)
- 1型(分母含s的一次方),ω從-90°出發(Im負軸),回到-270°(Im正軸)
- 2型(分母含s的二次方),ω從-180°出發(Re負軸),回到-270°(Im正軸)
系統為例,把三個系統的穿越頻率ωc放在重合的位置,給出如下圖示。
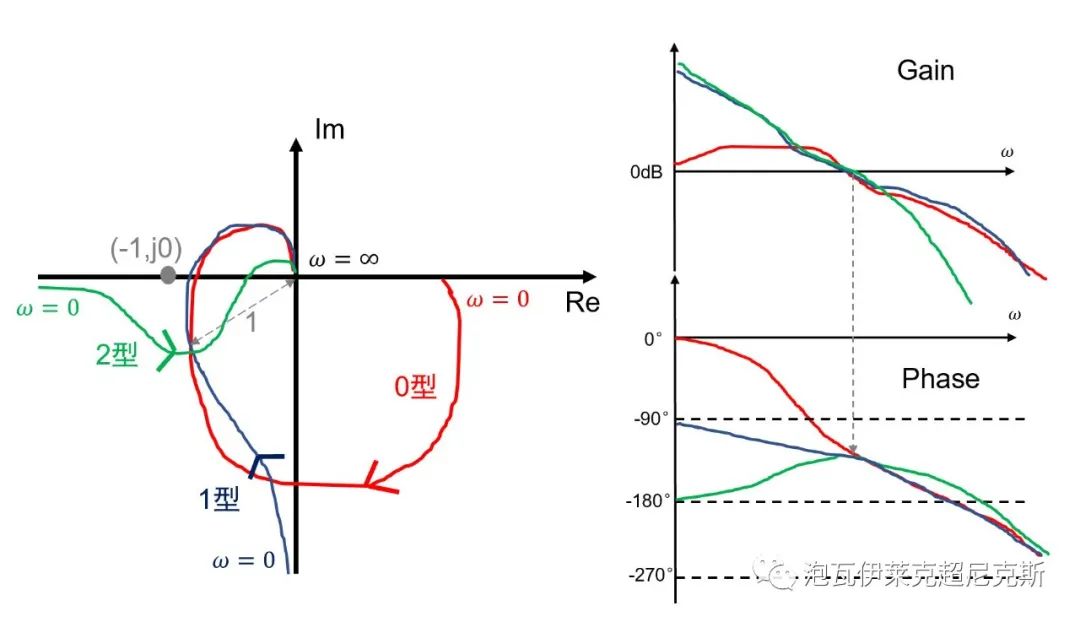
由圖,三者的相位裕量PM≈45°相同,增益裕量GM則是綠色的2型系統大,紅色0型和藍色1型系統小。
- 結論:
典型形狀的奈奎斯特圖,對應到波特圖時,穩定裕量GM/PM的物理意義是非常明確的,便于穩定裕量的定義,和穩定性判據的使用。
非典型系統→增益裕量無窮大
考察開環傳遞函數
G=s/(1+s)
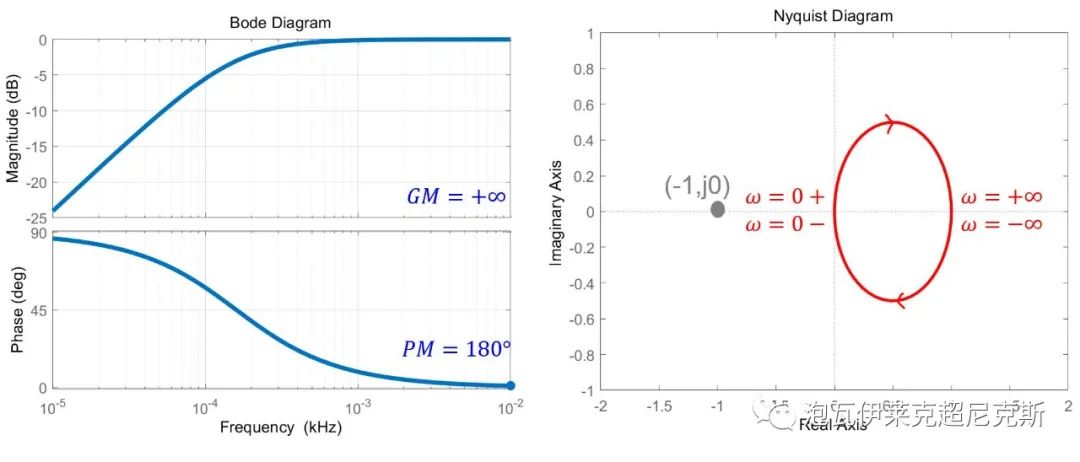
奈奎斯特圖的增益無論如何增大,奈奎斯特圖也不會包圍(-1,j0),故有GM=+∞;奈奎斯特圖與Re正軸交點是(1,j0),故有PM=180°。
再看波特圖,與奈奎斯特圖相對應,我們找不到幅頻曲線與0dB交點,也找不到相頻曲線與-180°交點。只能認為,頻率無窮大處幅頻與0dB相交,此時可以推出PM=180°;而相頻永遠不與-180°相交,所以GM=+∞。
考察開環傳遞函數
G=1/(s s (s+1))
這種系統是2型系統中的“結構不穩定”系統:若其分子增益和分母中一階子系統的時間常數可調,無論如何調參,其閉環以后均不能穩定。

由奈奎斯特圖可知,Z=N+P=1+0=1,閉環系統不穩定,且可以看出相位裕量PM為負,GM的話只有=-∞才有可能讓極坐標圖穿越(-1,0)。
再看波特圖,PM為負是明確的;同時相頻在頻率為0處與-180°相交,故GM=-∞。
- 結論:
當相頻不與-180°明顯相交,僅從波特圖觀察穩定裕量GM并不十分直觀。
局限1→幅頻多次穿越0dB
考察開環傳遞函數
G=2*(s+0.05) (s+0.1)/(s (s+1)*(s+0.5))

波特圖的幅頻曲線,多次穿越0dB,給相位裕量PM的認定造成困擾。
由奈奎斯特圖可知,Z=N+P=0+0=0,閉環系統穩定,增益裕量GM=+∞。
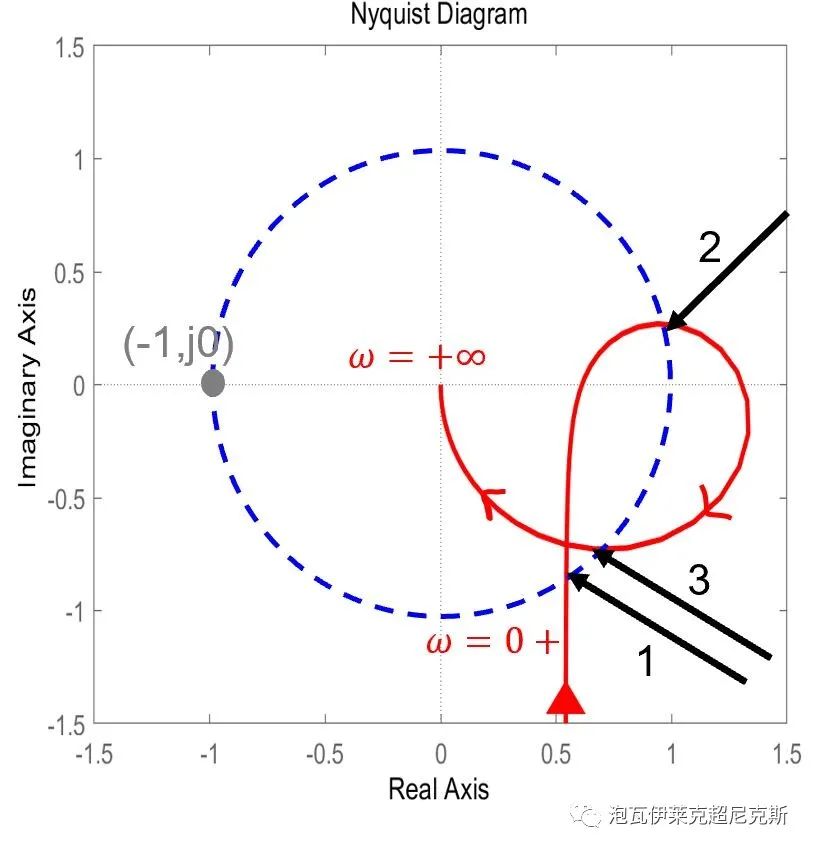
系統在頻率1,頻率2,頻率3處依次穿越0dB線,當曲線順時針旋轉到頻率1的位置與(-1,j0)相交后,系統已經開始不穩定。因此,相位裕量PM由頻率1處(最小的穿越頻率)的相角決定。
然而,倘若奈奎斯特曲線如下,當曲線順時針旋轉到頻率3的位置與(-1,j0)相交后,系統已經開始不穩定。因此,相位裕量PM由頻率3處(最大的穿越頻率)的相角決定。
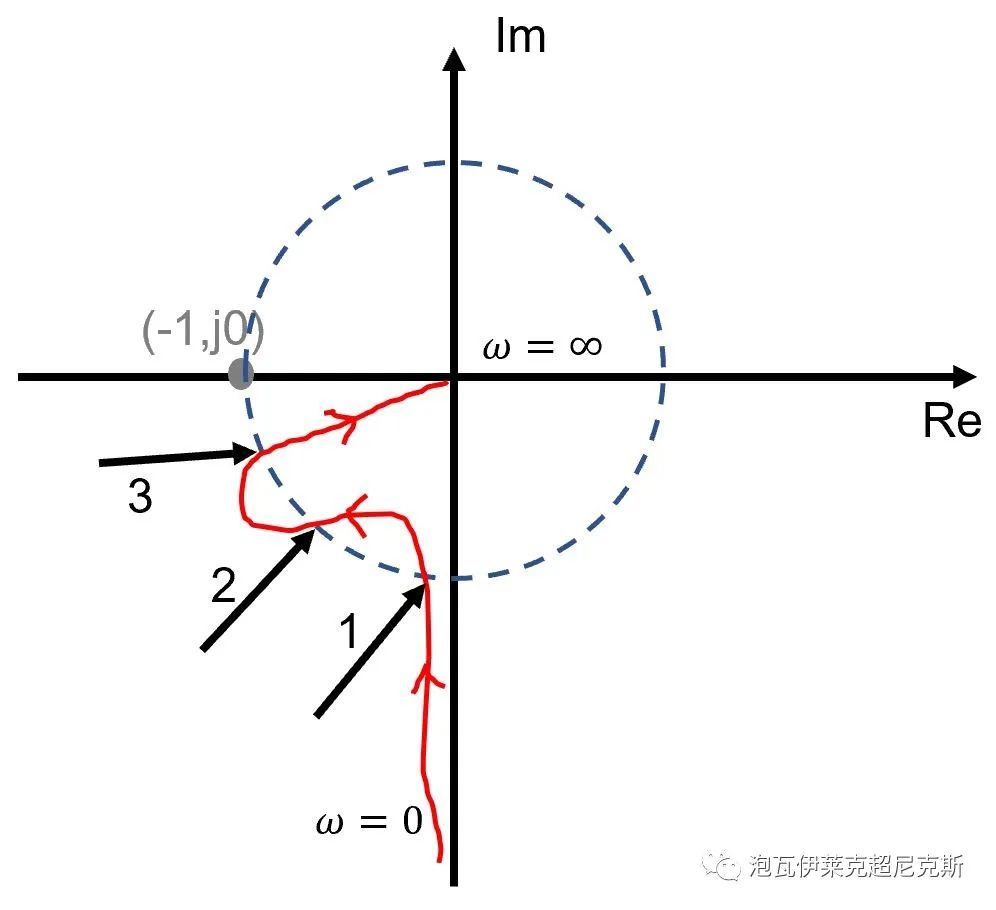
- 結論:
幅頻多次穿越0dB,相位裕量PM可能由最小或者最大穿越頻率處決定,取決于奈奎斯特圖的具體形狀。
局限2→相頻多次穿越-180°
考察開環傳遞函數
G=15*(s+5)(s+15)/((ss+s+1) (s+0.5) (0.01*s+1))
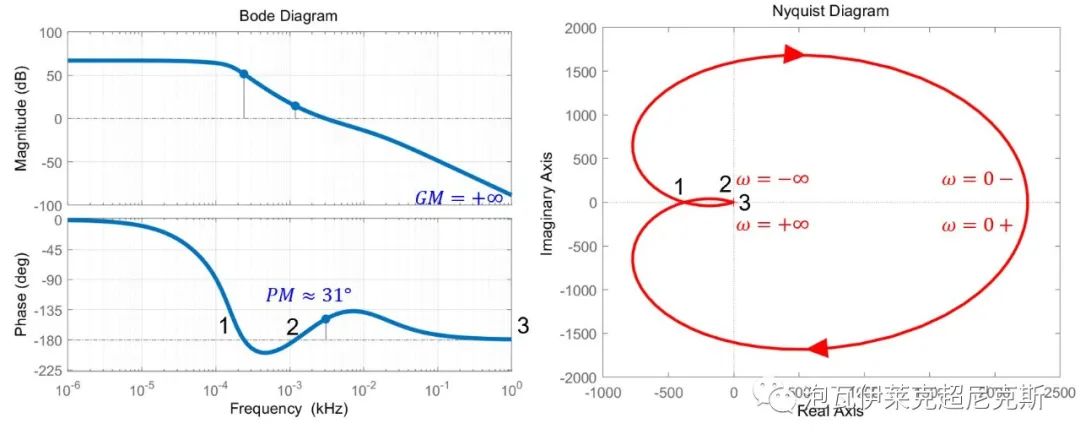
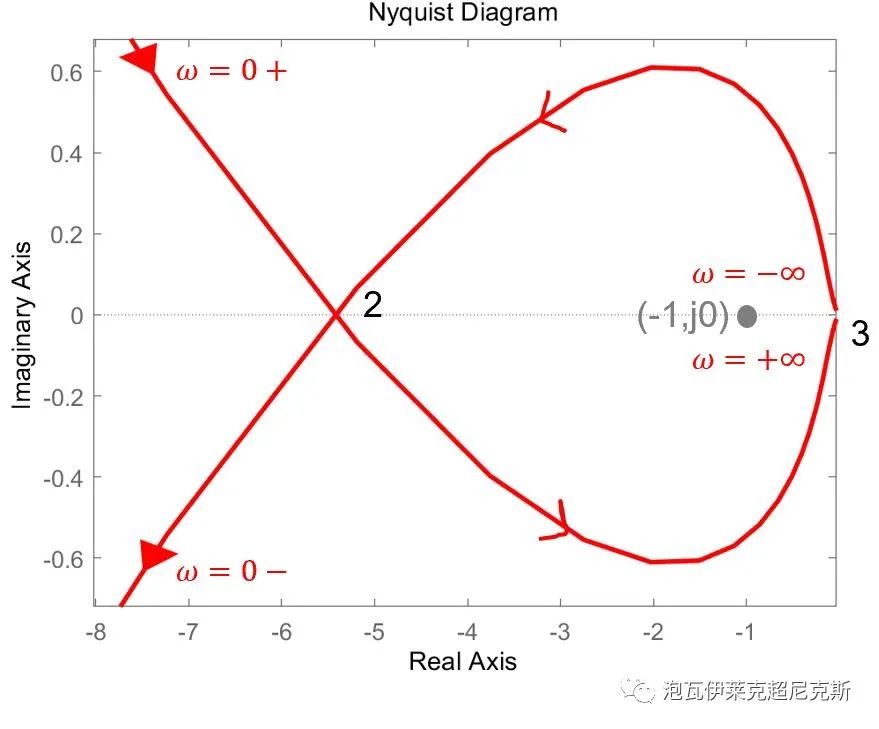
放大奈奎斯特圖(-1,j0)附近穿越的細節,以觀察頻率2和頻率3:
該例波特圖中,相位裕度PM=31°是易見的,但相頻曲線, 多次穿越-180°,給增益裕量GM的認定造成困擾 。
由該例的奈奎斯特圖可知,Z=N+P=-1+1+0=0,閉環系統穩定,且應該得到增益裕量GM=+∞。
然而,上例只是特例,更普遍的,多次穿越-180°,形似該形狀的奈奎斯特曲線可稱作"條件穩定"系統。如下,(-1,j0)可能位于如下箭頭指向的四個區間(1左側,1-2,2-3,3-4)。
若(-1,j0)在頻率1左側,則存在若干的不連續增益區間,使系統穩定。這樣一來,增益裕量GM是無法定義的:不存在一個GM,使得系統增益超過它后就不穩定,因為一個更大的增益區間會使系統又重新穩定。
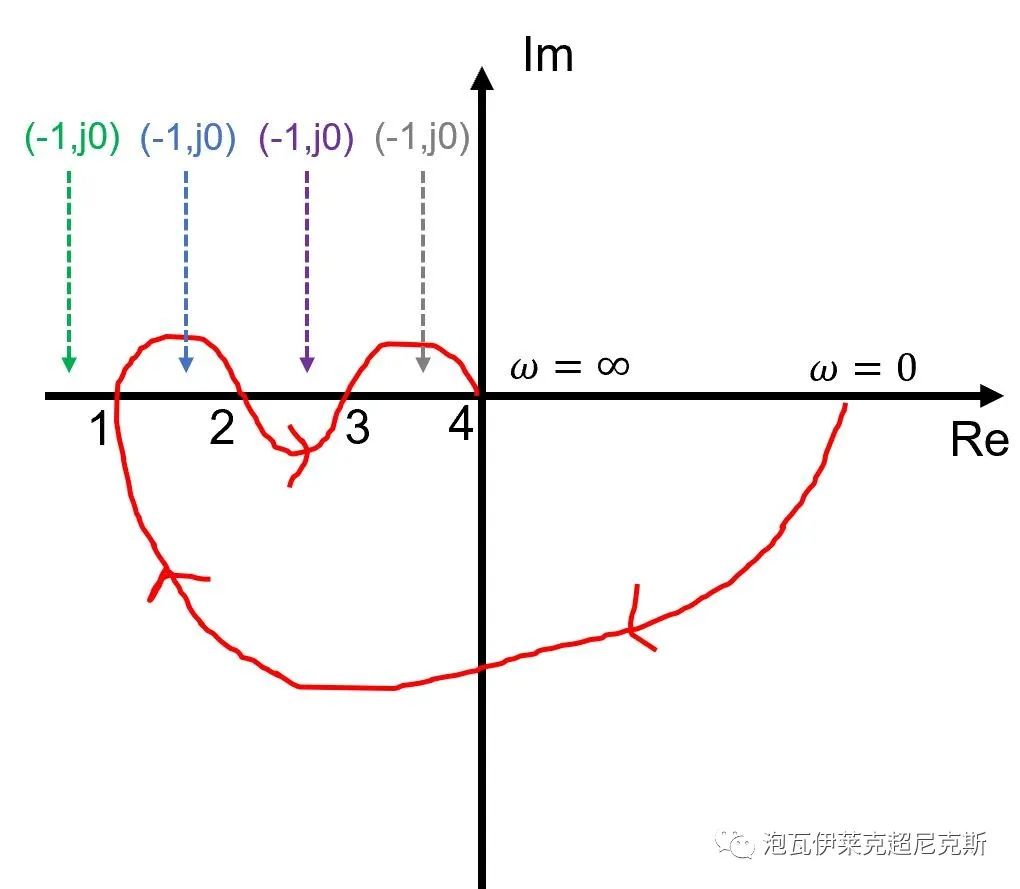
- 結論:
幅頻多次穿越-180°,若是“條件穩定”系統,增益裕量GM無法定義,失去物理意義。
失效→增益裕量GM<0才穩定
考察開環傳遞函數(非最小相位)
G=5*(s+3)/(s*(s-1))

由波特圖,**增益裕量GM=-14dB<0, **相位裕度PM=51.6°>0,根據判據,判為閉環不穩定系統嗎?
再看奈奎斯特圖,由于開環函數G含有一個右半平面不穩定極點,即P=1,那么Z=N+P=-1+1=0,閉環系統穩定!
- 結論:
存在開環不穩定的非最小相位系統,其波特圖穩定裕量判據是:增益裕量GM<0,相位裕量PM>0。
總結
基于波特圖的穩定裕量和穩定性判據,僅僅是針對典型系統的“工程性”簡化方法。
奈奎斯特圖才是判斷系統絕對穩定性和相對穩定性的有效頻域工具。
*注: 奈奎斯特穩定性判據在不同資料中形式不盡相同,本文采用的定義如下。
Z為閉環系統不穩定的極點個數,Z=0代表閉環系統穩定; P為開環函數不穩定極點數,N為完整正負頻域的閉合奈奎斯特曲線包圍(-1,j0)的帶符號圈數總和,順時針計為+,逆時針計為-。
-
奈奎斯特
+關注
關注
0文章
9瀏覽量
9274 -
增益天線
+關注
關注
0文章
13瀏覽量
7680 -
頻率儀
+關注
關注
0文章
12瀏覽量
5452 -
次奈奎斯特采樣
+關注
關注
0文章
3瀏覽量
5359
發布評論請先 登錄
相關推薦
如何運用波特圖的力量來確保電路穩定性
運放的穩定性仿真分析

環路增益的穩定性
模擬IC公司專家寫的波特圖詳解,放大器穩定補償
模擬IC公司專家寫的波特圖詳解,放大器穩定補償
系統開環判斷閉環穩定性
判定系統穩定性的充分必要條件是什么?
淺析環路穩定性原理與DCDC Buck環路穩定性
TCP/RED模型的穩定性分析
弱電網條件下基于阻抗的穩定性判據重塑
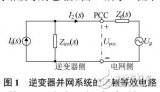
直流微電網穩定性分析
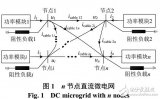
獨立電力系統靜態穩定性分析
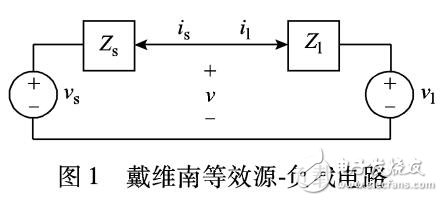




 波特圖穩定性判據為何存在嚴重的使用局限?
波特圖穩定性判據為何存在嚴重的使用局限?










評論