信號在頻域能夠呈現出時域不易發現的性質和規律，傅里葉變換是將信號從時域變換到頻域，便于在頻域對信號的特性進行分析。離散傅里葉變換 (DFT)，是傅里葉變換在時域和頻域上的離散呈現形式，通俗的說就是將經過采樣的有限長度時域離散采樣序列變換為等長度的頻域離散采樣序列，通過對變換得到的頻域采樣序列進行適當的換算和處理，可以得到信號的頻譜（頻率-幅值曲線和頻率-相位曲線）。

1. 定義

離散傅里葉變換 (DFT)的定義為：

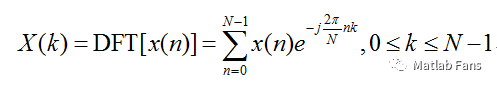
式中，x(n)為時域離散采樣序列（通常為實數序列），N為時域離散采樣序列x(n)的長度，X(k)為頻域離散采樣序列（通常為復數序列）。

快速傅里葉變換（FFT）是離散傅里葉變換（DFT）的一種快速算法，FFT的計算結果與DFT完全相同，但FFT相對于DFT減小了計算量、節約計算資源消耗，能夠適應在線計算，因此實際DFT都是通過FFT算法來求得結果。

Matlab軟件自帶fft函數實現快速傅里變換算法，但是光使用fft并不能直接得到信號的頻譜，還需要解決以下問題：

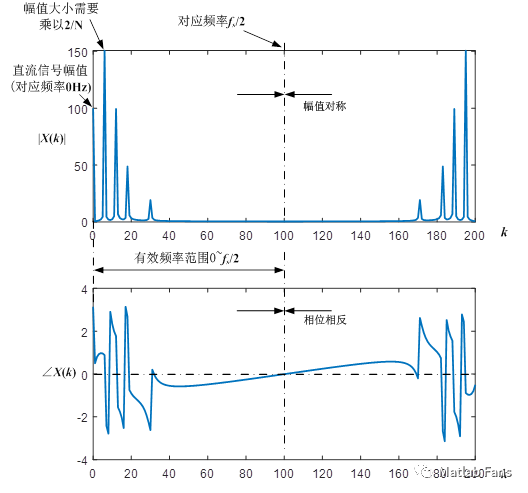
• 幅值變換 ：X(k)序列的幅值大小與參與變換的時域序列x(n)長度N有關，變換后的幅值|X(k)|需要乘以2/N得到真實幅值；
• 有效頻率區域 ：X(k)序列由兩部分共軛復數序列組成（復數共軛表示幅值相等、相位相反），相當于只有一半的復數序列是獨立有效的，這部分復數序列對應0~fs/2的頻率區域（fs為時域離散采樣序列x(n)的采樣頻率）。
• ** 直流信號的處理** ：直流信號幅值（對應頻率0Hz）為兩部分共軛復數序列在頻率0Hz處的加和，其真實幅值再乘以2/N后還需要再除以2得到真實的直流信號幅值。

2. 函數

初學的朋友若不理解上述變換和處理技巧，很難得到正確的頻譜圖。為此作者在fft函數的基礎上，使用Matlab開發了函數 DFT.m ，通過函數來實現上述幅值變換、有效頻率區域和直流信號的處理，能夠直接分析出給定離散信號x(n)的幅值譜和相位譜，函數簡單、易用、通用性好。

function [f,X_m,X_phi] = DFT(xn,ts,N,drawflag)
% [f,X_m,X_phi] = DFT(xn,ts,N,drawflag) 離散序列的快速傅里葉變換，時域轉換為頻域
% 輸入  xn為離散序列 為向量  
%       ts為序列的采樣時間/s
%       N為FFT變換的點數，默認為xn的長度  
%       drawflag為繪圖標識位，取0時不繪圖，其余非0值時繪圖，默認為繪圖
% 輸出 f為頻率向量
%      X_m為幅值向量
%      X_phi為相位向量，單位為°
% 注意計算出來的0頻分量(直流分量應該除以2)  直流分量的符號應結合相位圖來確定

3. 演示

3.1 單頻正弦信號（整數周期采樣）

%% Eg 1 單頻正弦信號
ts = 0.01;
t = 0:ts:1;
A = 1.5;       % 幅值  
f = 2;         % 頻率
w = 2*pi*f;    % 角頻率
phi = pi/3;    % 初始相位 
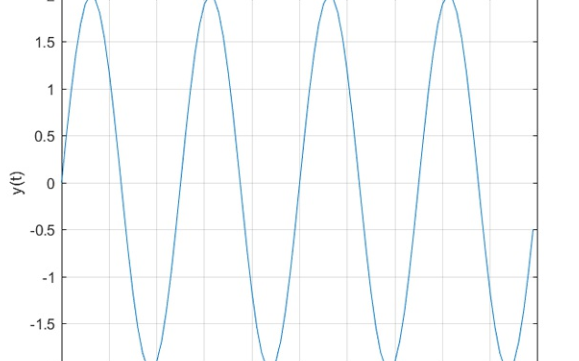
x = A*cos(w*t+phi);   % 時域信號
figure
plot(t,x)
xlabel('時間/s')
ylabel('時域信號x(t)')
% DFT變換將時域轉換到頻域,并繪制頻譜圖
[f,X_m,X_phi] = DFT(x,ts);

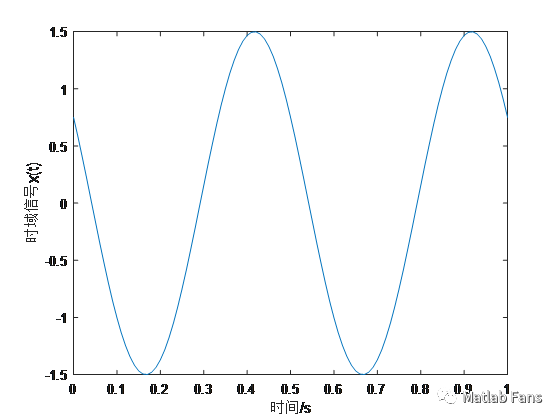
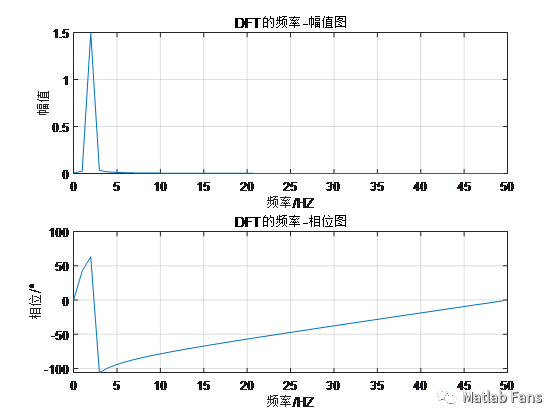
結果 ：

正弦信號頻率為2Hz，頻譜分析頻率為1.98Hz
正弦信號幅值為1.5，頻譜分析幅值為1.495
正弦信號相位為60°，頻譜分析相位為63.32°

**3.2 **單頻正弦信號（非整數周期采樣）

%% Eg 2 單頻正弦信號(非整數周期采樣)
ts = 0.01;
t = 0:ts:1;
A = 1.5;       % 幅值  
f = 1.5;         % 頻率
w = 2*pi*f;    % 角頻率
phi = pi/3;    % 初始相位 
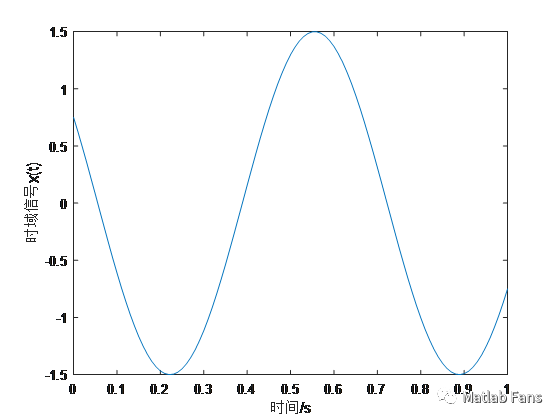
x = A*cos(w*t+phi);   % 時域信號
figure
plot(t,x)
xlabel('時間/s')
ylabel('時域信號x(t)')
% DFT變換將時域轉換到頻域,并繪制頻譜圖
[f,X_m,X_phi] = DFT(x,ts);

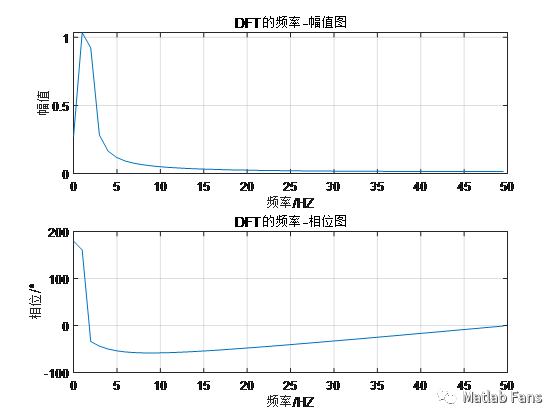
結果 ：

正弦信號頻率為1.5Hz，頻譜分析頻率為0.99Hz、1.98Hz
正弦信號幅值為1.5，頻譜分析幅值為1.034、0.923
正弦信號相位為60°，頻譜分析相位為160.93°、-33.76°

總結：

DFT變換后頻率序列的最小單位刻度為f s /N（此例為1Hz），非整數周期采樣時關心信號的頻率（此例為1.5Hz）不是頻率分辨率f s /N的正整數倍，那這個頻率成分信號會由前后兩個正整數倍的頻率成分信號（此例為1Hz和2Hz）的線性組合來替代，這就是頻譜泄漏現象，非周期采樣時某頻率成分信號向兩側頻率分辨率正整數倍的頻點泄漏。實際頻譜分析時并不清楚所關心的頻率點精確值，避免此問題的一個解決方法是，取更多的點參加DFT，即時域序列x(n)長度N值取長一些，讓頻率分辨率f s /N很小，以減小頻譜泄漏現象。再看下例。

%% Eg 2 單頻正弦信號(非整數周期采樣)
ts = 0.01;
t = 0:ts:1;
A = 1.5;       % 幅值  
f = 1.5;         % 頻率
w = 2*pi*f;    % 角頻率
phi = pi/3;    % 初始相位 
x = A*cos(w*t+phi);   % 時域信號
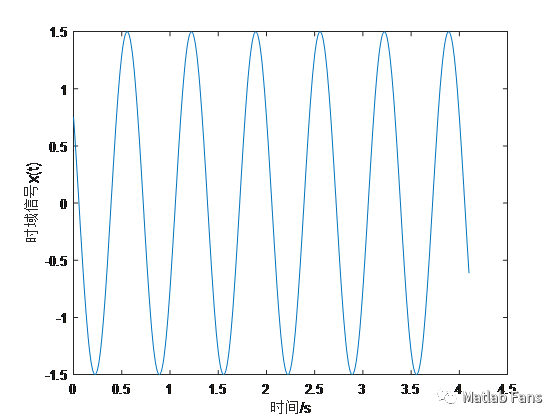
figure
plot(t,x)
xlabel('時間/s')
ylabel('時域信號x(t)')
% DFT變換將時域轉換到頻域,并繪制頻譜圖
[f,X_m,X_phi] = DFT(x,ts);

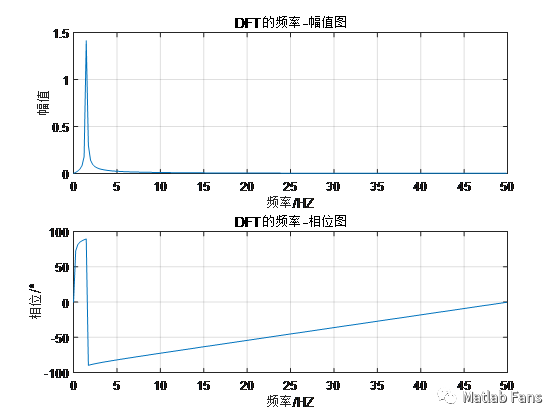
結果： 頻譜泄漏情況大為改善，采樣點繼續增多時，頻譜泄漏會進一步減小。

正弦信號頻率為1.5Hz，頻譜分析頻率主要成分為1.46Hz、
正弦信號幅值為1.5，頻譜分析頻率主要成分對應幅值為1.41
正弦信號相位為60°，頻譜分析頻率主要成分對應相位為89.5°

3.3 含有直流分量的單頻正弦信號

%% Eg 3 含有直流分量的單頻正弦信號
ts = 0.01;
t = 0:ts:1;
A = 1.5;       % 幅值  
f = 5;         % 頻率
w = 2*pi*f;    % 角頻率
phi = pi/6;    % 初始相位 
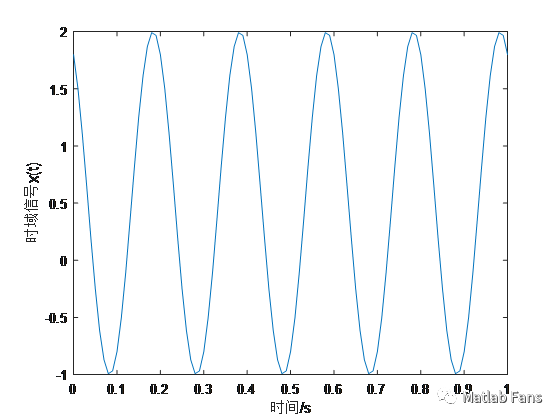
x = 0.5 + A*cos(w*t+phi);   % 時域信號,帶有直流偏移0.5
figure
plot(t,x)
xlabel('時間/s')
ylabel('時域信號x(t)')
% DFT變換將時域轉換到頻域,并繪制頻譜圖
[f,X_m,X_phi] = DFT(x,ts);

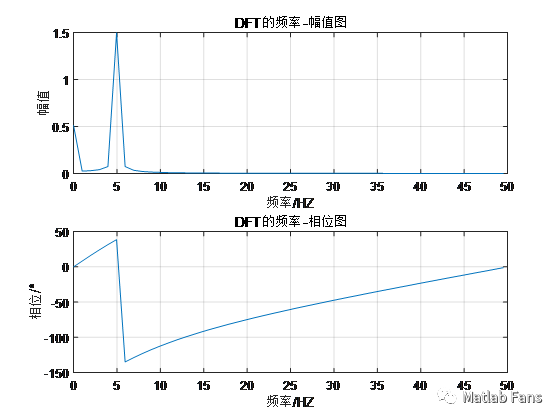
結果 ：

正弦信號頻率為5Hz，頻譜分析頻率為4.95Hz
正弦信號幅值為1.5，頻譜分析幅值為1.498
正弦信號相位為30°，頻譜分析相位為38.66°
正弦信號直流分量0.5，頻譜分析直流分量為0.51

**3.4 **正弦復合信號

%% Eg 4 正弦復合信號
ts = 0.01;
t = 0:ts:2;
A = [1.5 1 0.5 0.2];    % 幅值  
f = [3 6 9 15];         % 頻率
w = 2*pi*f;             % 角頻率
phi = (1:4)*pi/4;       % 初始相位 
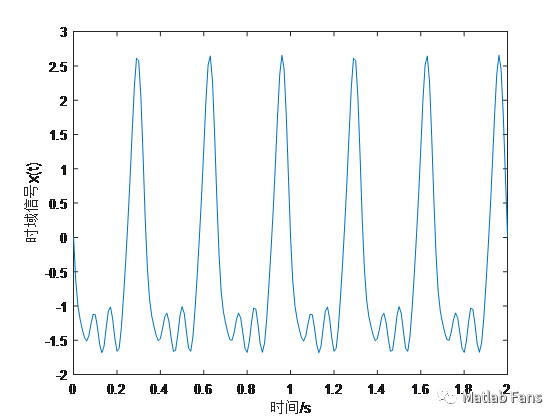
x = -0.5 + A(1)*cos(w(1)*t+phi(1)) + A(2)*cos(w(2)*t+phi(2)) + A(3)*cos(w(3)*t+phi(3)) + A(4)*cos(w(4)*t+phi(4));     % 時域信號
figure
plot(t,x)
xlabel('時間/s')
ylabel('時域信號x(t)')
% DFT變換將時域轉換到頻域,并繪制頻譜圖
[f,X_m,X_phi] = DFT(x,ts);

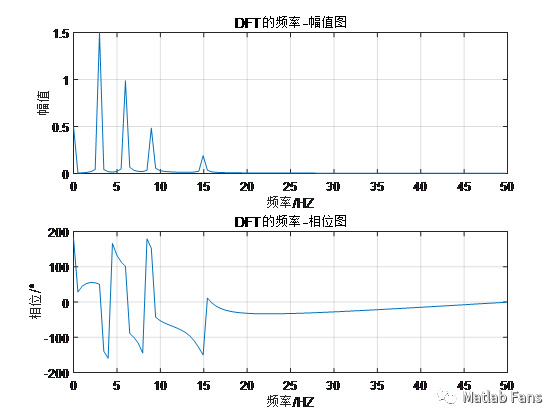
結果 ：

正弦信號頻率為3、6、9、15Hz，頻譜分析頻率為2.985、5.97、8.96、14.93Hz
正弦信號幅值為1.5、1、0.5、0.2，頻譜分析幅值為1.499、0.989、0.485、0.192
正弦信號相位為45°、90°、135°、180°，頻譜分析相位為50.6°、101.5°、152.9°、210°
正弦信號直流分量-0.5，頻譜分析直流分量為-0.497

注意 ：頻率為0Hz時對應的直流信號的幅值的正負號，是通過零頻相位來確定的，相位為0°表示幅值為正，相位為180°表示幅值為負。

**3.5 **含有隨機干擾的正弦信號

%% Eg 5 含有隨機干擾的正弦信號
ts = 0.01;
t = 0:ts:2;
A = [1 0.5];    % 幅值  
f = [3 10];         % 頻率
w = 2*pi*f;             % 角頻率
phi = (1:2)*pi/3;       % 初始相位 
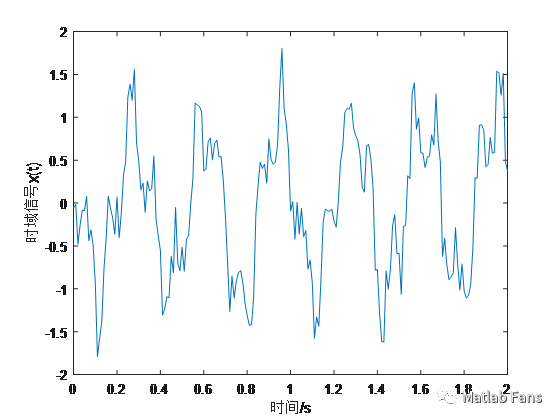
x =  A(1)*cos(w(1)*t+phi(1)) + A(2)*cos(w(2)*t+phi(2)) + 0.8*(rand(size(t))-0.5);     % 時域信號
figure
plot(t,x)
xlabel('時間/s')
ylabel('時域信號x(t)')
% DFT變換將時域轉換到頻域,并繪制頻譜圖
[f,X_m,X_phi] = DFT(x,ts);

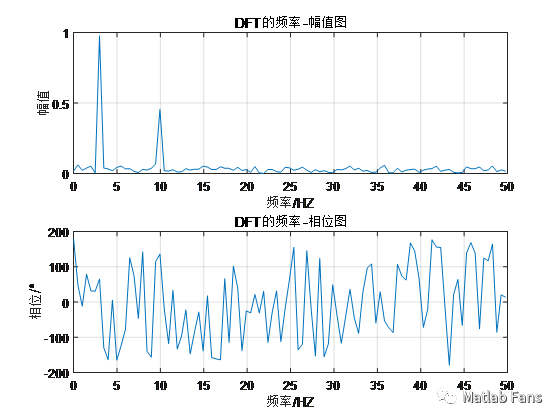
結果 ：

正弦信號頻率為3、10Hz，頻譜分析頻率為2.985、9.95Hz
正弦信號幅值為1、0.5，頻譜分析幅值為0.978、0.456
正弦信號相位為60°、135°，頻譜分析相位為65.1°、139.8°

**3.6 **實際案例

load data
ts = 0.001;
x = Jsd;
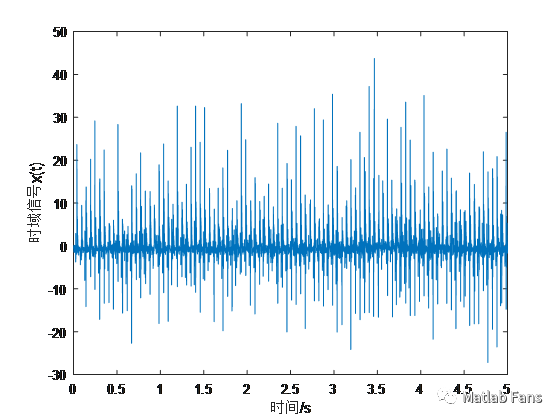
t = [0:length(x)-1]*ts;
figure
plot(t,x)
xlabel('時間/s')
ylabel('時域信號x(t)')
% DFT變換將時域轉換到頻域,并繪制頻譜圖
[f,X_m,X_phi] = DFT(x,ts);

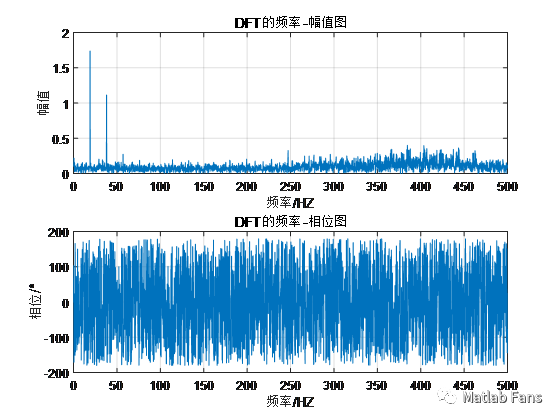
結果 ：

頻譜分析主要頻率成分為18.996、37.992Hz
頻譜分析主要頻率成分對應幅值為1.741、1.117

該項目為作者在強振環境下測得加速度信號，加速度是機械結構周期運動激勵產生，需要通過頻譜分析獲取機械結構周期運動的頻率。由于噪聲幅度遠大于有效信號幅度，信號的信噪比很低，從時域上很難辨別機械結構周期運動的頻率。但經過DFT后，從頻域上可以看出信號的主要頻率成分為19Hz和其倍頻38Hz，可以判斷機械結構周期運動的頻率為19Hz，38Hz為結構響應的非線性特性所產生的倍頻。