前面的幾篇文章分別分享了PID算法的原理、增量式和位置式PID算法的區別、以及過程控制中一些重要的指標，感興趣的朋友可以回看之前的文章或者自行查閱資料。

在實際項目中，使用數字PID算法對系統的被控量進行控制的時候，有時候并不是僅僅的使用簡單的增量式或者位置式的PID就完成了對系統的被控量控制。很多時候會采用一些改進了的PID算法進行系統的控制，以求達到更好的控制效果。

常見的對標準PID算法進行改進的措施有哪些呢？下面會根據我個人有限的經驗進行簡單的分享，就當是一次學習分享吧！

1、針對微分項的改進

對微分項的改進常見的有兩種措施：微分先行和輸入濾波。

（1）微分先行

我們知道，在一個閉環的控制系統中，即使我們期望被控量穩定在期望的值范圍內它也不可能是絕對的穩定的，變化才是常態，所以才要考慮才要某些算法進行調控，比如PID算法就很常用。

而微分先行的改進措施就是：在PID算法中把對偏差微分改為對被控量的微分。

這是什么意思呢？因為對于很多的系統而言，就算在給定的輸入值發生了變化，也不會引起被控量的輸出發生大幅度的變化。這就是說在輸入值發生變化的時候，被控量也是在一段時間范圍內緩慢進行變化的，是不會發生突變的。

那么既然被控量不會因為輸入值的突變而發生突變，所以微分先行就是把原本算法中由對偏差的微分變為對被控量的變化的微分。這樣的做法就是在即使輸入量發生變化偏差還未產生時，微分就已經在起作用了，從而緩慢變化到新的輸入值所要求的輸出值。

所以，微分先行的輸出增量計算如下：

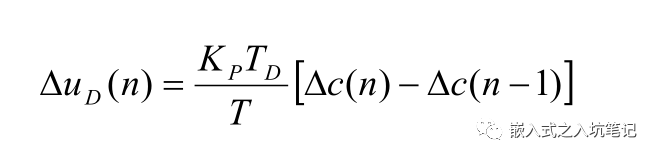
（2）輸入濾波

輸入濾波的做法就是在計算微分項的時候，不直接采用當前時刻的誤差e(n) 進行計算，而是采用經過濾波之后的濾波值。

這個濾波是怎么進行的呢？一般的做法是：用過去的三個采樣時刻的誤差和當前時刻的誤差共四個誤差值求一個平均值，再通過加權求和的方式構成微分項。

2、針對積分項的改進

對于積分的作用我前面的文章是有講過的，在PID算法中，積分可以消除系統的靜差，讓被控量偏離期望輸出值的偏差減小。但是積分作用它本身也有一個副作用，因為積分是對偏差的累積，可能會引起積分飽和的情況。

積分飽和又是什么呢？積分飽和指的是在一個PID調控的系統中，如果偏差一直存在的情況下，積分會一直對偏差進行累積，可能會導致積分項變得很大。

積分飽和又會對PID調控的系統帶來什么樣的影響呢？打個比方：如果積分飽和了，在系統的偏差方向發生了改變了之后，PID這個時候會起作用進行調節，但是由于積分項太大了，就需要經過比較長的時間才能讓輸出U(n) 從積分飽和區脫離，會使調控作用滯后，讓系統出現明顯的超調，整個系統的調節效果會變差，這肯定是不希望出現的。

所以需要一些措施對抗積分飽和。常見的克服積分飽和的方法有下面的方式：

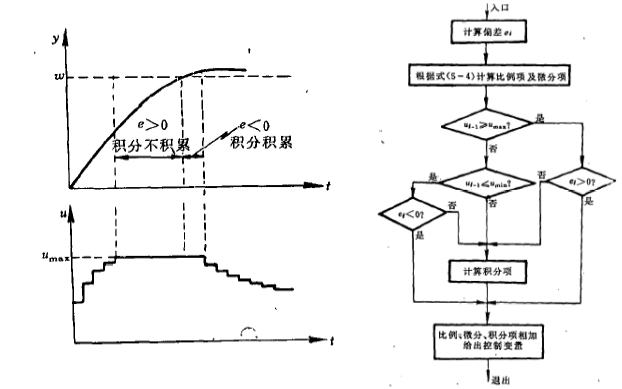
（1）積分限幅法

積分限幅法的操作原理是：對積分項的輸出設定一個限制，當積分項的輸出達到限制，就停止積分項的計算，PID算法中的積分計算項的值采用上一個時刻的積分值。這樣是為了防止積分項的輸出過大，讓系統的調節時間變慢，影響系統品質。

積分限幅的計算實現步驟一般如下圖：

（2）積分分離法

上面提到了積分限幅的方式，就是讓積分項的輸出不要過大，防止控制時間變化太慢。還有一種做法就是將積分分離出來。

積分分離的做法就是：對系統的偏差設定一個門限值，如果系統偏差的絕對值小于門限值，就進行積分累加；相反，如果系統的偏差的絕對值大于這個門限值，就不進行積分。這樣也可以避免過度積分的問題，防止系統因為偏差過大時產生了過大的控制作用。

積分分離的計算步驟如下：

（3）變速積分法

變速積分法的基本實現原理是：當系統的偏差比較大的時候，讓積分的速度慢一些；相反，當系統的偏差比較小的時候，讓積分的速度快一些，以求盡快的消除靜差。

這種操作方式時，積分項按照下面的方式計算：

上面的計算中，A為設定的一個偏差閾值。

3、補充數字PID的其他需要注意的問題

（1）積分的不靈敏區

數字PID算法的應用大多數都是通過微處理器實現的，所以即使同樣的算法放在不同的微處理器系統中產生的效果也是不一樣的。

之所以會出現積分不靈敏的情況，是跟微處理的運行字長和計算精度有關的。比如當一個微處理器的運行字長較短時，如果采樣周期很短，但是積分時間又比較長，這個時候就會容易因為字長太小精度不夠，導致偏差不明顯或者不出現，讓積分的作用消失了。這就是積分不靈敏的情況。

（2）數字PID采樣周期的選擇問題

根據前面的數字PID的計算公式中會發現，公式中有一個變量Ti，這個就是采樣周期。

一般而言，采樣周期越小，數字PID就越是精確，控制效果就越接近連續控制。但是呢，天下萬物都是有正反兩面的，采樣周期小了控制效果是精確了，但是太過頻繁的采樣就必然是要占用跟多的計算時間，計算機的計算負擔就會變重，對計算機的運算性能要求就更高。

那采樣頻率要怎么選擇才合適呢？

這個時候就要先看看采樣定理了，也就是“香農采樣定理”或“奈奎斯特采樣定理”。

采樣定理：在進行模擬/數字信號的轉換過程中，當采樣頻率fs.max大于信號中最高頻率fmax的2倍時(fs.max >= 2fmax)，采樣之后的數字信號完整地保留了原始信號中的信息，一般實際應用中保證采樣頻率為信號最高頻率的5~10倍。

所以，最大的采樣周期公式如下：

關于PID算法的一些改進就分享到這里，因為是個人實際使用中的總結，可能會有理解錯誤的地方，如有錯漏，還煩請指正。