引言
時(shí)空數(shù)據(jù)是復(fù)雜而又多樣化的數(shù)據(jù),分析時(shí)空數(shù)據(jù)能為人類天氣預(yù)測(cè)(如華為盤古大模型)、地質(zhì)起伏預(yù)測(cè)、太陽黑子預(yù)測(cè)、紅綠燈優(yōu)化調(diào)度、共享單車投放規(guī)劃等方面帶來重大影響。然而時(shí)空數(shù)據(jù)又是復(fù)雜的,體現(xiàn)在其數(shù)據(jù)的時(shí)空變換和空間異質(zhì),而其數(shù)據(jù)分布也極其極端 -- 存在大量的零值,以及數(shù)據(jù)體現(xiàn)長(zhǎng)尾分布。
今天要介紹的便是通過引入Tweedie分布和Zero-inflated負(fù)二項(xiàng)分布去捕捉零膨脹效應(yīng)和長(zhǎng)尾效應(yīng)的復(fù)雜時(shí)空數(shù)據(jù),結(jié)合時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò),來衡量預(yù)測(cè)的不確定性。
01
介紹
1.1
不確定性衡量
想象一下,當(dāng)我們踏入人工智能這片廣袤領(lǐng)域,仿佛邁入一片神秘森林,其中充滿了機(jī)器智能和前沿科技的奧秘。在這充滿活力的領(lǐng)域中,存在一個(gè)至關(guān)重要的概念,需要我們一同深入探索,那便是不確定性衡量。或許你正在引導(dǎo)一臺(tái)智能計(jì)算機(jī)學(xué)會(huì)識(shí)別各種動(dòng)物,像是讓它分辨狗、貓、大象等。但是,當(dāng)它面對(duì)一張全新的動(dòng)物圖片時(shí),需要做的不僅是做出判斷,還有告訴我們它對(duì)自己的判斷有多有信心,這個(gè)信心便是——不確定性。
這個(gè)過程引發(fā)了一個(gè)有趣的問題:在計(jì)算機(jī)模型做出預(yù)測(cè)時(shí),如何讓我們知道它有多確信這個(gè)預(yù)測(cè)是準(zhǔn)確的呢?這涉及到一個(gè)核心概念,即模型的不確定性。模型的不確定性涉及它在進(jìn)行預(yù)測(cè)時(shí)可能出現(xiàn)錯(cuò)誤或產(chǎn)生不確定結(jié)果的程度。這種不確定性可能來源于兩個(gè)方面,一個(gè)是模型接觸到的數(shù)據(jù)有限,另一個(gè)是模型自身的復(fù)雜性導(dǎo)致它無法始終做出準(zhǔn)確預(yù)測(cè)。
首先,我們來考慮模型所面臨的數(shù)據(jù)不確定性。就如同當(dāng)你只看過幾張貓和狗的照片后,被要求辨認(rèn)一種你從未見過的奇特動(dòng)物一樣,模型也可能在面對(duì)全新、未曾接觸過的數(shù)據(jù)時(shí)感到困惑。畢竟,模型所了解的知識(shí)來自于它在訓(xùn)練時(shí)接觸到的數(shù)據(jù),它難以直接將這些知識(shí)應(yīng)用于陌生情境。這就好比你只見過黑色和白色的狗,突然間面對(duì)一只藍(lán)色的狗,你也會(huì)感到困惑吧?
其次,還有模型本身的不確定性,也就是模型的局限性。假設(shè)你要教計(jì)算機(jī)區(qū)分貓和狗,你指示它關(guān)注尾巴的長(zhǎng)度、耳朵的形狀等特征。但是,如果你給它一張模糊的圖片,它可能無法精確判斷。因?yàn)槟P筒⒉荒芟袢祟愐粯訌哪:木€索中推斷出合理結(jié)論,它可能因?yàn)?a target="_blank">信息不足而做出錯(cuò)誤預(yù)測(cè)。
為了克服這些不確定性,研究者們提出了一些方法,使我們能更好地理解模型的預(yù)測(cè)。例如,模型可以輸出一個(gè)預(yù)測(cè)的置信度,就好像是它告訴你“我對(duì)這個(gè)預(yù)測(cè)很有信心”或者“我對(duì)這個(gè)預(yù)測(cè)不太確定”。另一種方法是,模型可以輸出一個(gè)預(yù)測(cè)的分布,顯示每個(gè)可能結(jié)果的概率。這種方法類似于擲骰子,你了解每個(gè)面的概率,從而更好地預(yù)測(cè)結(jié)果。
通過這些方法,我們可以更清晰地理解模型預(yù)測(cè)時(shí)的不確定性,就像是在未知的森林中多了一張地圖,幫助我們更自信地踏出每一步。這一概念在醫(yī)學(xué)、交通、金融等領(lǐng)域都有廣泛應(yīng)用,讓我們能更明智地利用模型的預(yù)測(cè),做出更可靠的決策。
1.2
時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)
Spatial-Temporal Graph Neural Network
時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)是近年來在深度學(xué)習(xí)領(lǐng)域異軍突起的一項(xiàng)強(qiáng)大工具,為我們理解和處理涉及時(shí)空關(guān)系的數(shù)據(jù)開辟了嶄新視角。比方說,我們想分析城市中的交通流量變化,或者預(yù)測(cè)未來氣象的演變,這些任務(wù)涉及到時(shí)間和空間的錯(cuò)綜復(fù)雜聯(lián)系。時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)就如同一把鑰匙,為我們敞開了探索時(shí)空數(shù)據(jù)的大門。
首先,我們來解釋一下時(shí)空數(shù)據(jù)是什么。時(shí)空數(shù)據(jù)包括了時(shí)間和空間信息,比如在不同時(shí)間和地點(diǎn)的溫度、交通流量、人口分布等。而時(shí)空?qǐng)D則是一種用來展示時(shí)空數(shù)據(jù)中關(guān)系和相互作用的圖結(jié)構(gòu)。在這個(gè)圖中,節(jié)點(diǎn)代表不同的地點(diǎn)或物體,邊代表它們之間的關(guān)聯(lián)。
時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)是專為處理時(shí)空?qǐng)D數(shù)據(jù)而設(shè)計(jì)的深度學(xué)習(xí)模型。它結(jié)合了圖神經(jīng)網(wǎng)絡(luò)和時(shí)間序列預(yù)測(cè)的思想,能夠幫助我們從復(fù)雜的時(shí)空數(shù)據(jù)中提取有價(jià)值的信息。這些網(wǎng)絡(luò)可以捕捉地點(diǎn)之間的關(guān)系,同時(shí)也能追蹤隨時(shí)間變化的模式,這樣我們就能更準(zhǔn)確地預(yù)測(cè)未來、分析趨勢(shì),甚至優(yōu)化決策。
舉個(gè)例子來說,想象一個(gè)城市的交通系統(tǒng)。每個(gè)路口可以被視為一個(gè)節(jié)點(diǎn),而車輛在不同時(shí)刻穿越這些路口則形成了邊。時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)可以學(xué)習(xí)交通流量在不同路口、不同時(shí)間之間的變化規(guī)律,這有助于城市規(guī)劃者更好地優(yōu)化交通流動(dòng),減少擁堵。
這種網(wǎng)絡(luò)結(jié)構(gòu)在很多領(lǐng)域都有廣泛應(yīng)用。在氣象學(xué)中,時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)可以分析全球各地的氣象數(shù)據(jù),幫助氣象學(xué)家更精準(zhǔn)地預(yù)測(cè)氣候變化。在醫(yī)療領(lǐng)域,它可以處理醫(yī)療設(shè)備產(chǎn)生的時(shí)空數(shù)據(jù),用于疾病預(yù)測(cè)和診斷。在金融領(lǐng)域,它可以分析不同市場(chǎng)之間的關(guān)系,幫助投資者做出更明智的決策。
1.3
概率模型
在數(shù)據(jù)分析的舞臺(tái)上,我們時(shí)常會(huì)面對(duì)一些特殊情況,這些情況使得傳統(tǒng)統(tǒng)計(jì)方法不再足夠。其中兩種常見情形分別是長(zhǎng)尾數(shù)據(jù)和零膨脹數(shù)據(jù)。這些數(shù)據(jù)背后隱藏著復(fù)雜的分布特征,傳統(tǒng)統(tǒng)計(jì)模型可能難以妥善應(yīng)對(duì)。而此時(shí),概率模型如 Zero-inflated負(fù)二項(xiàng)分布 和 Tweedie分布 就發(fā)揮了關(guān)鍵作用。
長(zhǎng)尾數(shù)據(jù)意味著數(shù)據(jù)分布中存在著許多數(shù)值較小但數(shù)量龐大的極端值,這些值往往對(duì)模型產(chǎn)生重大影響。比如,分析社交媒體上的點(diǎn)贊數(shù)或銷售數(shù)據(jù)中的銷售量時(shí),傳統(tǒng)的均值和方差等統(tǒng)計(jì)量可能無法完全揭示分布的特性。
零膨脹數(shù)據(jù)則是數(shù)據(jù)中零值的數(shù)量遠(yuǎn)超預(yù)期的情況。舉例而言,當(dāng)我們分析醫(yī)療保險(xiǎn)索賠數(shù)據(jù)時(shí),大部分人可能沒有提出索賠,導(dǎo)致數(shù)據(jù)中有大量的零值。然而,傳統(tǒng)模型可能因?yàn)槠浼僭O(shè)與實(shí)際情況不符而表現(xiàn)不佳。
長(zhǎng)尾和零膨脹效應(yīng)在時(shí)空數(shù)據(jù)上體現(xiàn)極為明顯,以 O-D flows數(shù)據(jù)(任意兩地在任意事件的車流量值)為例:

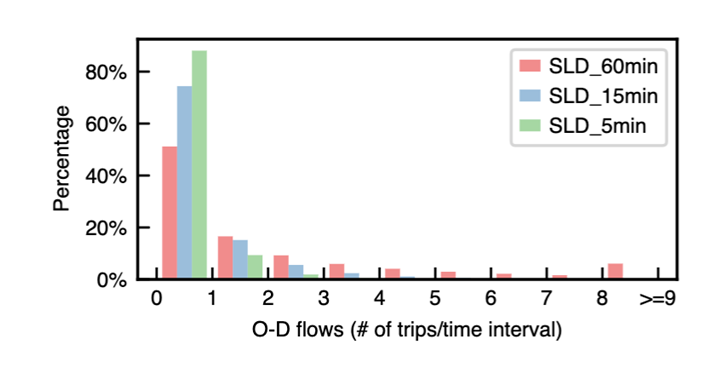
可以看到在SLD_60min, SLD_15min, SLD_5min這三個(gè)數(shù)據(jù)集上,零值幾乎占據(jù)了大多數(shù),而大于2的情況所占比例非常少,又明顯體現(xiàn)了“長(zhǎng)尾”的特點(diǎn)。
為了更好地解決這些問題,Zero-inflated負(fù)二項(xiàng)分布 和 Tweedie分布應(yīng)運(yùn)而生。
Zero-inflated 負(fù)二項(xiàng)分布可以看作是兩種分布的結(jié)合體:負(fù)二項(xiàng)分布(用于計(jì)數(shù)數(shù)據(jù)的離散分布)和零膨脹分布(用于描述數(shù)據(jù)中零值較多的情況)。這種分布適用于數(shù)據(jù)中不僅存在大量零值,還可能出現(xiàn)較大值的情形。利用這個(gè)模型,我們能夠更精確地捕捉數(shù)據(jù)分布的特點(diǎn),從而更好地進(jìn)行預(yù)測(cè)和分析。
Tweedie 分布則屬于廣義線性模型中的概率分布,適用于處理長(zhǎng)尾數(shù)據(jù)和零膨脹數(shù)據(jù)。其特點(diǎn)之一是廣泛適用范圍,能夠應(yīng)對(duì)連續(xù)數(shù)據(jù)、離散數(shù)據(jù)、混合數(shù)據(jù)等多種情況。通過調(diào)整Tweedie分布的參數(shù),我們可以更好地?cái)M合實(shí)際數(shù)據(jù)的分布。
這些概率模型在解決長(zhǎng)尾數(shù)據(jù)和零膨脹數(shù)據(jù)問題上發(fā)揮了重要作用。它們不僅有助于更精確地描述和理解特殊類型數(shù)據(jù),還為數(shù)據(jù)分析和預(yù)測(cè)提供了更強(qiáng)大的工具。醫(yī)療、金融、社會(huì)科學(xué)等領(lǐng)域都廣泛應(yīng)用這些模型,為數(shù)據(jù)分析帶來了更多可能性。
02
算法介紹
2.1
分布介紹
負(fù)二項(xiàng)分布(Negative Binomial Distribution)
負(fù)二項(xiàng)分布是統(tǒng)計(jì)學(xué)上一種離散概率分布,用于描述在重復(fù)試驗(yàn)中獲得固定數(shù)量的成功所需的獨(dú)立失敗次數(shù)的分布。這個(gè)分布經(jīng)常用來描述不定次數(shù)的成功事件,例如在多次投擲硬幣直到獲得一定數(shù)量的正面朝上為止。
與二項(xiàng)分布不同,二項(xiàng)分布描述的是進(jìn)行固定次數(shù)試驗(yàn)中成功次數(shù)的分布,而負(fù)二項(xiàng)分布則關(guān)注在獲得固定數(shù)量成功之前所需的試驗(yàn)次數(shù)。負(fù)二項(xiàng)分布在許多實(shí)際場(chǎng)景中都有應(yīng)用,比如在金融中用于分析投資成功前的失敗次數(shù),或者在生物學(xué)中用于研究實(shí)驗(yàn)成功前需要多少次不成功的嘗試。這個(gè)分布提供了一種數(shù)學(xué)工具,幫助我們理解和解釋各種隨機(jī)事件中的概率分布。
滿足以下條件的稱為負(fù)二項(xiàng)分布:實(shí)驗(yàn)包含一系列獨(dú)立的實(shí)驗(yàn),每個(gè)實(shí)驗(yàn)都有成功、失敗兩種結(jié)果,成功的概率是恒定的,實(shí)驗(yàn)持續(xù)到n次不成功,n為正整數(shù)。切換到我們的時(shí)空數(shù)據(jù)中,成功即數(shù)據(jù)非0,失敗即數(shù)據(jù)為0。
其概率分布如下:
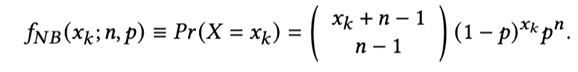
這里的 n 和 p 是模型參數(shù),分別表示成功的次數(shù)和單次失敗的概率。
零膨脹負(fù)二項(xiàng)分布(Zero-InflatedNegative
Binomial Distribution)
然而,現(xiàn)實(shí)世界中的數(shù)據(jù)通常會(huì)出現(xiàn)許多零觀測(cè)值。零值的激增加劇了負(fù)二項(xiàng)分布參數(shù)的學(xué)習(xí)。因此,引入了一個(gè)新的參數(shù)來學(xué)習(xí)零值膨脹率,從而得到了零膨脹負(fù)二項(xiàng)分布。
零膨脹負(fù)二項(xiàng)分布(Zero-Inflated Negative Binomial Distribution,簡(jiǎn)稱ZINB 分布)是一種概率統(tǒng)計(jì)學(xué)中的概率分布,用于處理數(shù)據(jù)中存在大量零值的情況,同時(shí)考慮了負(fù)二項(xiàng)分布的特性。
在現(xiàn)實(shí)世界的數(shù)據(jù)中,往往會(huì)有很多零值的存在,這可能是因?yàn)槟承┨囟ㄔ驅(qū)е碌摹@纾谏缃幻襟w上的點(diǎn)贊數(shù)量中,很多帖子可能沒有被點(diǎn)贊,導(dǎo)致數(shù)據(jù)中存在許多零值。然而,傳統(tǒng)的負(fù)二項(xiàng)分布在處理這種情況時(shí)可能表現(xiàn)不佳,因?yàn)樗鼰o法很好地捕捉到數(shù)據(jù)中的零值特征。
ZINB 分布的引入就是為了更好地處理這種零值問題。它結(jié)合了兩個(gè)部分:一個(gè)用于描述零值的部分,另一個(gè)用于描述非零值的部分。具體而言,ZINB分布中引入了一個(gè)額外的參數(shù),用于表示數(shù)據(jù)中零值的膨脹程度。在生成數(shù)據(jù)時(shí),有的概率產(chǎn)生零值,而有的概率遵循負(fù)二項(xiàng)分布生成非零值。這樣,ZINB分布能夠更準(zhǔn)確地刻畫存在零值的數(shù)據(jù)特征,并在建模和分析過程中更加適用。
其概率分布如下:
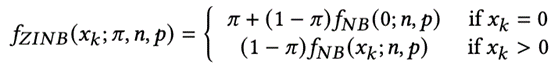
在負(fù)二項(xiàng)分布的基礎(chǔ)上,考慮了零值的加權(quán)。這里的pi即為零膨脹系數(shù)。
ZINB 分布在許多領(lǐng)域的數(shù)據(jù)分析中都有應(yīng)用,特別是在處理存在大量零值的數(shù)據(jù)集時(shí),如社交媒體數(shù)據(jù)、醫(yī)療數(shù)據(jù)等。通過引入零膨脹參數(shù),ZINB 分布幫助我們更好地理解和解釋這些特殊類型的數(shù)據(jù),并提供了更準(zhǔn)確的分析工具。
Tweedie 分布
負(fù)二項(xiàng)分布是對(duì)零值做了一定的處理,但不能適用于極度零值的情況;因此通過引入新參數(shù)來對(duì)零值做加權(quán),加強(qiáng)了模型魯棒性。然而,有過多零值的出現(xiàn),就一定會(huì)有長(zhǎng)尾效應(yīng)的產(chǎn)生,因此如何建模長(zhǎng)尾效應(yīng)也是一個(gè)值的考慮的問題 —— Tweedie 分布。
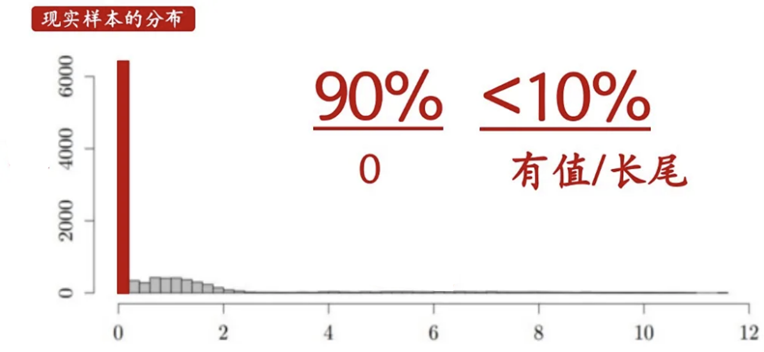
圖源知乎用戶:一直學(xué)習(xí)一直爽
Tweedie分布是一種概率統(tǒng)計(jì)學(xué)中的廣義線性模型,用于建模和分析具有復(fù)雜分布特征的正數(shù)數(shù)據(jù)。這種分布在描述連續(xù)、離散和混合數(shù)據(jù)等多種數(shù)據(jù)類型時(shí)都具有應(yīng)用價(jià)值。Tweedie分布由一系列的特殊情況組成,包括正態(tài)分布、伽馬分布、泊松分布等。它的靈活性使得它能夠適應(yīng)各種數(shù)據(jù)分布的特點(diǎn),而不需要對(duì)每種特定情況進(jìn)行單獨(dú)的建模。Tweedie分布的參數(shù)化形式取決于兩個(gè)主要參數(shù):指數(shù)參數(shù)和離散參數(shù)。指數(shù)參數(shù)決定了數(shù)據(jù)的分布形狀,離散參數(shù)則控制了數(shù)據(jù)的離散程度。通過適當(dāng)?shù)剡x擇這些參數(shù),可以使Tweedie分布擬合多種數(shù)據(jù)類型,包括長(zhǎng)尾數(shù)據(jù)和零膨脹數(shù)據(jù)。
Tweedie分布的概率密度函數(shù)如下:
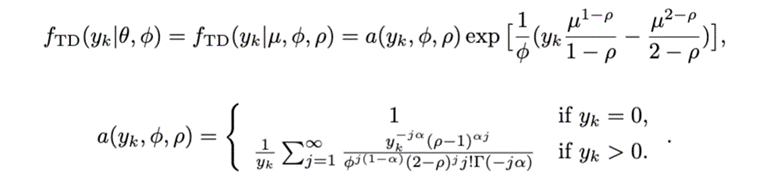
這里一共有三個(gè)參數(shù):離散系數(shù), 指數(shù)系數(shù)和模型均值。
在實(shí)際應(yīng)用中,Tweedie分布廣泛用于處理存在多樣性和復(fù)雜性的數(shù)據(jù)集,如保險(xiǎn)索賠數(shù)據(jù)、金融時(shí)間序列數(shù)據(jù)、生態(tài)學(xué)數(shù)據(jù)等。通過使用Tweedie分布,我們能夠更好地捕捉和解釋數(shù)據(jù)的分布特征,從而進(jìn)行更精確的分析、建模和預(yù)測(cè)。
綜上所述,為了更好地建模時(shí)空?qǐng)D的某一個(gè)時(shí)間點(diǎn)的某一個(gè)地理點(diǎn)的數(shù)據(jù)以及其不確定性,我們采用二參數(shù)模型(NB),三參數(shù)模型(ZINB和Tweedie)來計(jì)算模型的不確定性。
2.2
時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)介紹
如何建模每個(gè)分布的參數(shù)成為了一個(gè)棘手的問題,但在時(shí)空數(shù)據(jù)上,我們可以采用時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)來建模。
而為了學(xué)習(xí)這些參數(shù),我們使用了時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò)(STGNN)——這個(gè)神經(jīng)網(wǎng)絡(luò)的設(shè)計(jì)有點(diǎn)像是在解謎,它通過一個(gè)時(shí)間編碼器和一個(gè)空間編碼器來學(xué)習(xí)參數(shù)的值。
具體而言:時(shí)間編碼器使用了一種叫做門控循環(huán)單元(GRU)的技術(shù),類似于人類大腦中的一些運(yùn)作方式,來處理數(shù)據(jù)中的時(shí)間信息。
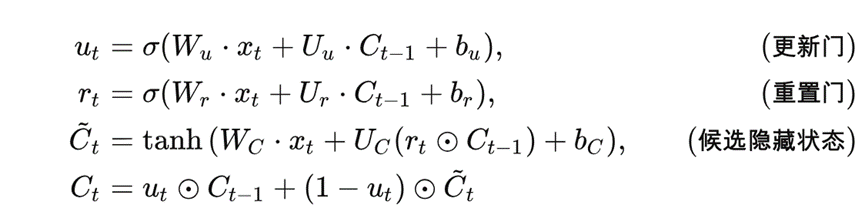
GRU 計(jì)算公式
而空間編碼器則使用了圖注意力網(wǎng)絡(luò)(GAT),就好像在數(shù)據(jù)之間建立了一種連接關(guān)系,幫助我們更好地理解數(shù)據(jù)之間的關(guān)聯(lián)性。
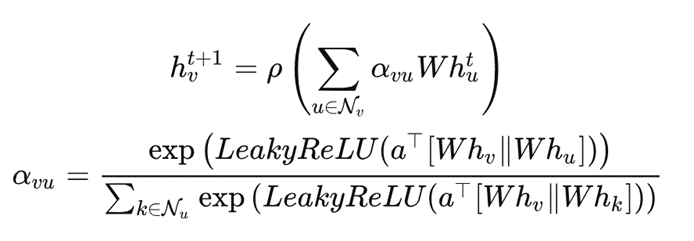
GAT 計(jì)算公式
其STGNN網(wǎng)絡(luò)框架如下:
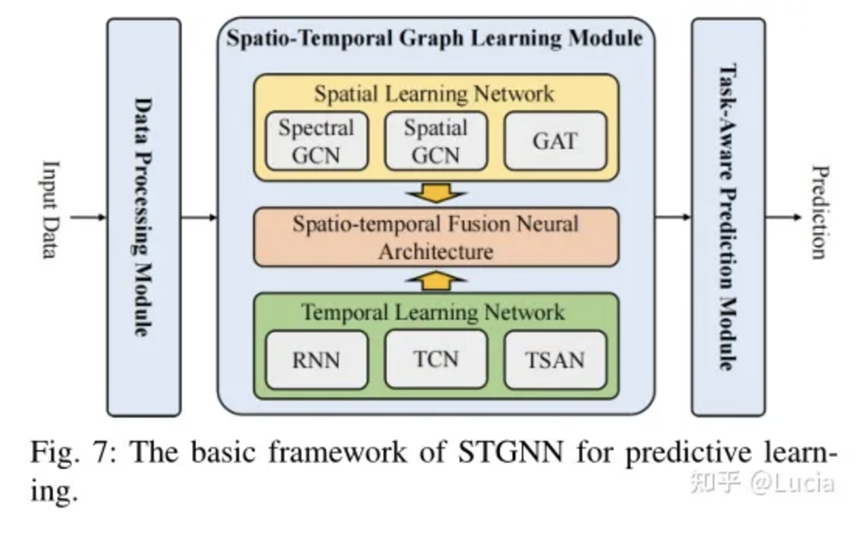
圖來自知乎用戶:Lucia
通過這個(gè)特殊的時(shí)空?qǐng)D神經(jīng)網(wǎng)絡(luò),我們能夠更準(zhǔn)確地學(xué)習(xí)數(shù)據(jù)模型中的參數(shù)(二參數(shù)、三參數(shù)等),基于該參數(shù)構(gòu)建結(jié)果分布,從而更好地分析數(shù)據(jù),做出更可靠的預(yù)測(cè)。這就像是在解謎一樣,不斷優(yōu)化網(wǎng)絡(luò),讓我們的數(shù)據(jù)分析變得更加精準(zhǔn)和有用。
2.3
模型訓(xùn)練指導(dǎo)函數(shù)
作者采用最大似然函數(shù)方法來指導(dǎo)模型訓(xùn)練。
最大化似然函數(shù)是一種在統(tǒng)計(jì)學(xué)和概率論中常用的方法,用于找到最適合數(shù)據(jù)的參數(shù)值,以便使得數(shù)據(jù)出現(xiàn)的概率最大化。
讓我們用一個(gè)簡(jiǎn)單的例子來解釋這個(gè)概念。假設(shè)你有一堆骰子擲出的數(shù)據(jù),你想要找出這個(gè)骰子是均勻的還是有偏的。你知道這個(gè)骰子有6個(gè)面,但你不知道每個(gè)面出現(xiàn)的概率。你可以用一個(gè)參數(shù)來表示每個(gè)面出現(xiàn)的概率,然后構(gòu)建一個(gè)概率模型。
現(xiàn)在,你有了一些實(shí)際擲骰子得到的數(shù)據(jù),比如說你投了100次骰子,記錄下每次的結(jié)果。你的目標(biāo)是找到一個(gè)參數(shù),使得在這個(gè)參數(shù)下,投出這100次骰子的概率最大化。
這就是最大化似然函數(shù)的思想。似然函數(shù)表示的是,在給定參數(shù)的情況下,觀察到實(shí)際數(shù)據(jù)的概率。你要做的就是調(diào)整參數(shù),使得這個(gè)概率最大化,也就是讓觀察到的數(shù)據(jù)在模型下出現(xiàn)的概率最大化。
最大化似然函數(shù)是一種尋找最優(yōu)參數(shù)的方法,它在許多領(lǐng)域都有應(yīng)用,從機(jī)器學(xué)習(xí)到統(tǒng)計(jì)分析。通過找到最適合數(shù)據(jù)的參數(shù),我們能夠更好地理解數(shù)據(jù)的規(guī)律,從而做出更準(zhǔn)確的預(yù)測(cè)和決策。這個(gè)方法就像是在拼圖,我們不斷嘗試不同的拼法,以找到最符合實(shí)際情況的模型。
ZINB 最大似然函數(shù)
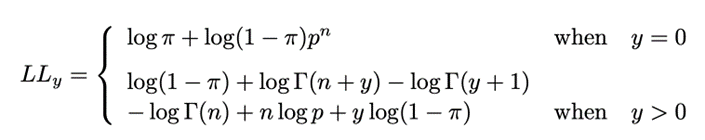
其中, , 均為通過STGNN學(xué)習(xí)所得,不斷得優(yōu)化該函數(shù),能達(dá)到模型的訓(xùn)練目的。
Tweedie 最大似然函數(shù)
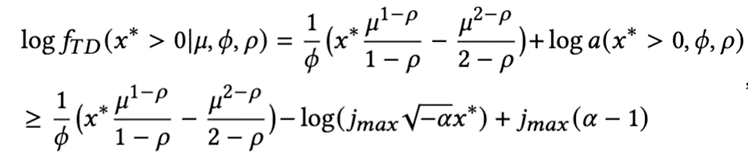
其中, , 均為通過STGNN學(xué)習(xí)所得,不斷得優(yōu)化該函數(shù),能達(dá)到模型的訓(xùn)練目的。
審核編輯:劉清
-
處理器
+關(guān)注
關(guān)注
68文章
19407瀏覽量
231186 -
編碼器
+關(guān)注
關(guān)注
45文章
3668瀏覽量
135243 -
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4779瀏覽量
101171 -
人工智能
+關(guān)注
關(guān)注
1796文章
47666瀏覽量
240288 -
Gru
+關(guān)注
關(guān)注
0文章
12瀏覽量
7504
原文標(biāo)題:基于時(shí)空?qǐng)D概率模型的不確定性衡量
文章出處:【微信號(hào):bdtdsj,微信公眾號(hào):中科院半導(dǎo)體所】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
如何創(chuàng)造可信任的機(jī)器學(xué)習(xí)模型?先要理解不確定性
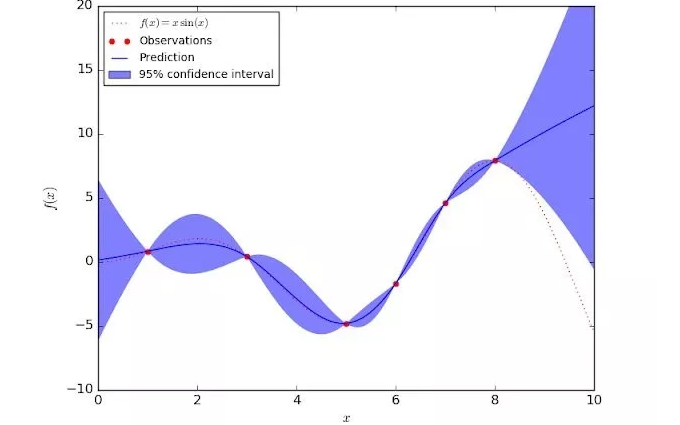




 基于時(shí)空?qǐng)D概率模型的不確定性衡量介紹
基于時(shí)空?qǐng)D概率模型的不確定性衡量介紹











評(píng)論