2.1 電路的等效
2.1.1 二端網絡
任何一個復雜的電路網絡, 如果向外引出兩個端鈕, 則稱為二端網絡 ( 一端口網絡)。網絡內部沒有獨立源的二端網絡,稱為無源二端網絡;反之,稱為有源二端網絡。
2.1.2 等效的概念
對于任何兩個二端網絡,盡管它們的內部結構可能不同,但只要它們端口處的電壓-電流關系完全相同,從而它們對聯接到該端口上的任一外部電路的作用效果相同,則這兩個二端網絡互為等效。
這里所謂“完全相同”的含義是指這一相同不應受外部電路的限制,即相同并不只是對某一特定的外部電路而言。
注意:這里的等效,只是指這個二端網絡對外部電路等效,在二端網絡內部是不等效的。
2.2 簡單電阻電路分析
2.2.1 電阻的串聯
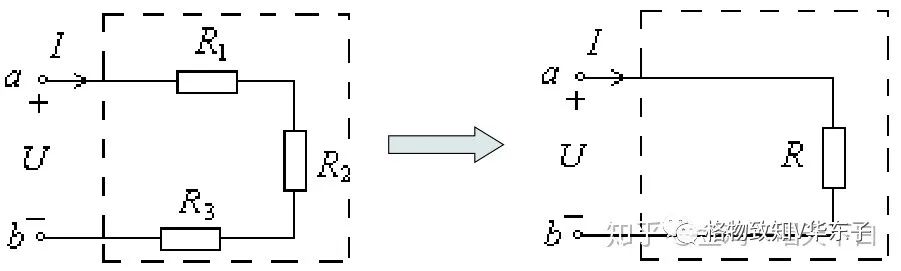
n個電阻串聯時,其等效電阻為 :

等效電阻:任一無源二端電阻網絡,在其二端施加獨立電源us(或is),輸入電流為i (或u),此網絡可等效為一個電阻,即等效電阻為R,其值為:
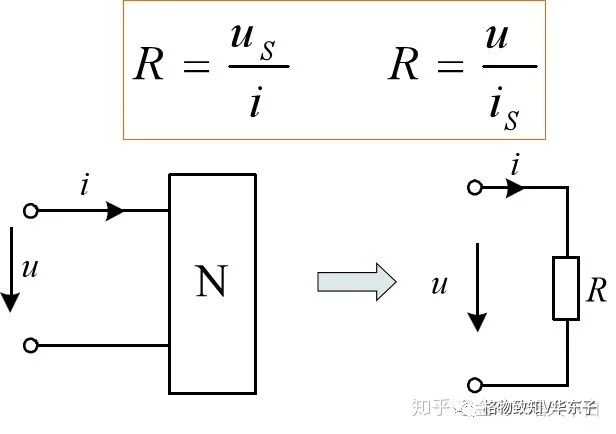
限流作用:端口電壓一定時,串聯電阻越多,電流越小,所以串聯電阻可以“限流”。
分壓作用:串聯的各電阻,其兩端電壓與自身電阻大小成正比,即
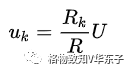
分壓公式
2.2.2 電阻的并聯

n個電阻并聯時,其等效電導為 :

兩個電阻的并聯公式:
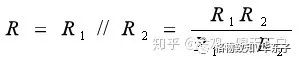
分流公式:并聯的各電阻中電流與各電阻大小成反比,即
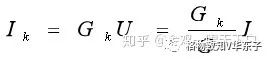
兩個電阻并聯的分流公式:
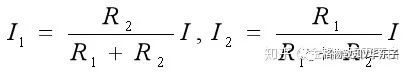
2.2.3 電阻的混聯
既有電阻元件串聯又有電阻元件并聯的電路稱為電阻元件的混聯。
如下圖所示電路:
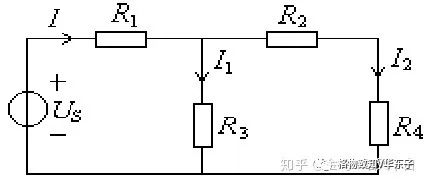
電源右端的網絡,等效電阻為:

2.2.4 電阻的三角形連接與星形連接

電阻的三角形連接 電阻的星形連接
等效變換:
等效變換的條件是對應端流入或流出的電流(I1 、I2、I3 )對應相等,對應端間的電壓(U1、U2、U3 )也對應相等。

特別的:如果  則有
則有

反過來如果  則有
則有
 2.3 含獨立源的簡單電路分析
2.3 含獨立源的簡單電路分析
2.3.1 電壓源與電流源之間的等效變換
等效變換的根據:對外電路來說,伏安關系完全相同。
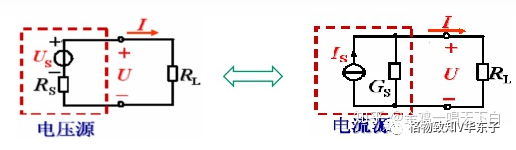
電壓源的伏安關系為: 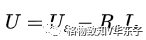
電流源的伏安關系為:
結論就是:等效的條件
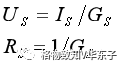
任何一個理想電壓源 Us 和一個電阻 Rs串聯的電路,都可化為一個電流為 Is 的理想電流源和這個電阻的并聯的電路,反之亦然。
兩種理想電源不能等效變換;等效變換時,兩電源的參考方向要一一對應。
2.3.2 電源串并聯電路的分析
1.任何一個網絡與一個理想電壓源相并聯,均可等效為這個理想電壓源;
2.任何一個網絡與一個理想電流源相串聯,均可等效為這個理想電流源;
3.n個理想電壓源串聯,可以等效為一個電壓源Us,且有
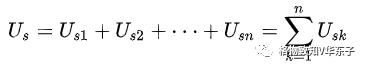
其中,Usk與Us方向一致時其值取正,反之取負。
4.n個理想電流源并聯,可以等效為一個電流源Is,且有
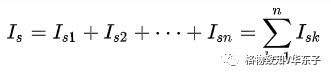
其中,Isk與Is方向一致時其值取正,反之取負。
注意:電壓源和電流源的等效關系只對外電路而言,對電源內部則是不等效的。
2.4 含受控源的簡單電路的分析
在分析電路時,受控源可當作獨立源一樣對待。電路基本定律和元件的伏安特性是分析此類電路的依據,也就是仍要用KCL、KVL和VCR。和獨立源所不同的是在電路中受控源不能象獨立源一樣作為獨立激勵,也就是這類電路不能只有受控源,而沒有獨立源(局部電路除外)。
2.4.1 受控源的等效變換
受控電壓源與電阻串聯組合形式可以和受控電流源與電阻并聯組合形式之間進行等效變換。
方法:與獨立源支路的等效變換基本相同。但變換時一定要注意不要消去控制量,只有先將控制量轉化為不會被消去的量以后,才能進行等效變換。
例題:求圖示二端網絡ab的等效電路。

2.4.2 含受控源的單回路電路和單結點偶電路分析
分析含受控源的簡單電路與分析不含受控源的電路方法是相同,只不過會多出控制量這一變量,把控制量用準備求解的變量表示,做為補充方程,方程數仍然是足夠的。
2.4.3 含受控源不含獨立源的二端網絡的等效電路
含受控源不含獨立源的二端電阻網絡可以等效為一個電阻。
方法是:在端口處施加一個電壓或施加電流,然后計算端口的伏安關系,從而求得該二端網絡的等效電阻。
例:求圖示電路對于端口的等效電阻。
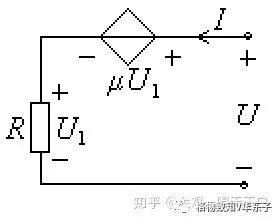
解:在圖示電路的端口處施加電壓U,然后寫出端口電流I與電壓U的關系式
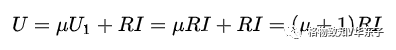
從而求得二端網絡的等效電阻為

進一步分析:顯然,由于受控源的存在,使端口等效電阻發生變化,等效電阻與參數 μ 相關。
① 二端網絡等效為一個電阻,說明該二端網絡從外電路吸收電能;
②若  ,則等效電阻小于零,為一負電阻。則這時,該二端網絡向外電路提供電能。出現負電阻的原因是由于網絡內含受控源,而受控源是可以提供電能的。
,則等效電阻小于零,為一負電阻。則這時,該二端網絡向外電路提供電能。出現負電阻的原因是由于網絡內含受控源,而受控源是可以提供電能的。
2.5 支路電流法
2.5.1 分析線性電路的一般方法
分析線性電路的一般方法:根據電路元件的伏安特性、歐姆定律、基爾霍夫定律等基本規律,通過列寫電路方程來求解電路電壓和電流的方法。這種電路方程的列寫方法有規律可循,具有一般性(對任何線性電路都適用),故稱為一般分析方法。
線性電路方程:通常是一組線性代數方程,非常適合于計算機去處理(解方程)。
復雜線性電路的一般分析法就是根據KCL、KVL及元件的電壓與電流關系列方程、解方程。根據列方程時所選變量的不同可分為支路電流法、回路電流法和節點電壓法。
一般分析方法的步驟:
① 選取一組合適的電路變量(如支路電流、網孔電流或節點電壓等)。
② 根據元件的電壓、電流關系特性(VCR)以及KCL、KVL建立一組獨立的電路方程。
③ 聯立求解方程中的變量。
這里的關鍵是建立的方程相互間是否獨立、以及方程數是否足夠。
2.5.2 支路電流法
我們以各支路電流為變量列寫方程、解方程的方法稱為支路電流法。
一般地說,對具有n個節點,b條支路的電路,只要列出b個獨立的電路方程,便可以求解這b個未知量。:
只有(n-1)個節點是獨立的,即只能列出(n-1)個KCL 方程;
對于平面電路而言,網孔數為[b -(n-1)]個,恰好為獨立回路數,即可列[b -(n-1)]個KVL方程。
因此應用KCL和KVL一共可列出 (n-1)+ [b-(n-1)]=b個獨立方程,即可解出b個支路電流。
使用支路電流法的工作步驟:
a.設定每一條支路的電流(  )并標注其參考方向;
)并標注其參考方向;
b. 在n個節點中選定一個參考節點,對其它各獨立節點列出(n-1)個 KCL方程;
c. 選取網孔,設定各網孔繞行方向;
d.對各網孔列出[b-(n-1)]個KVL方程 ;
e.聯立求解上述的b個獨立方程 ,得出并個待求的各支路電流。
可以看到,一個稍微復雜的電路,采用支路電流法列寫出的方程組是一個多元方程組,如果不借助于計算機,求解起來非常麻煩。實踐中,我們往往也并不需要知道每一條支路的電流,而是部分電流或電壓,這就需要我們思考,有沒有更簡潔的分析電路的方法。
2.6 網孔電流法
什么是網孔電流:沿著網孔邊界連續流動的假想電流。要注意,這是一個假想電流,并不是實際存在的,但它和每一條支路的實際電流有關系。
網孔電流法:就是以網孔電流為變量列寫方程、求解方程的一種電路分析方法。它僅適用于平面電路。
基本思想:為減少未知量(方程)的個數,假想每個網孔中有一個網孔電流。各支路電流可用網孔電流的線性組合表示,來求得電路的解。
網孔電流在網孔中是閉合的,對每個相關結點均流進一次,流出一次,所以網孔電流在所有節點處都自動滿足KCL,因此,只需列出[b -(n-1)]個KVL方程,就可以使得電路得到求解。網孔電流法中的變量—網孔電流個數就是網孔數[b -(n-1)]個。所以網孔電流是一組獨立變量。
使用網孔電流法的工作步驟:
① 選定各網孔電流的參考方向,也就是列方程式時這個網孔的繞行方向。
② 列寫 [m=b -(n-1)]個網孔的KVL方程。

其中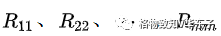 稱為網孔1-m的自電阻,為該網孔中所有電阻之和;
稱為網孔1-m的自電阻,為該網孔中所有電阻之和;
其余電阻為各個網孔之間的互電阻:計算方法是兩個相鄰網孔公共支路中所有電阻之和,不相鄰則互電阻為零);當通過該互電阻的兩個網孔電流的參考方向一致時,互電阻取正號;參考方向相反時,取負號。
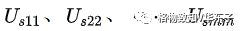 為網孔1-m中所有電源兩端電壓的代數和。注意此處,在求這個代數和時,如果某個電源電壓方向與繞行方向相同取負號,否則取正號。
為網孔1-m中所有電源兩端電壓的代數和。注意此處,在求這個代數和時,如果某個電源電壓方向與繞行方向相同取負號,否則取正號。
③ 聯立取求解網孔電流方程,得到網孔電流。
④ 指定待求支路電流的參考方向。此支路電流為與其相關的網孔電流的代數和,列寫方程,從而求出待求支路電流。
下面單獨說一下,含理想電流源支路時的求解方法:
如能使這個電流源中只有一個網孔電流流過,則該網孔電流就等于此電流源的電流,而不必對這個網孔列網孔方程了;
如不能使電流源中只有一個網孔電流流過。則需要把電流源的電壓也作為變量列入網孔方程,并將電流源電流與有關網孔電流的關系作為補充方程,方程數仍然足夠,就可以一并求解。
2.7 節點電壓法
節點電壓:確定某個節點作為參考節點(理論上那個節點都可以),則其余任意獨立節點到該參考節點的電壓,就成為該節點的節點電壓。
要注意,這是一個假想電壓,并不是實際存在的,但它和每一條支路的實際電壓有關系。
節點電壓法:就是以節點電壓為變量列寫方程、求解方程的一種電路分析方法。適用于節點較少的電路。
基本思想:選節點電壓為未知量,則KVL自動滿足,無需列寫KVL 方程。各支路電流、電壓可視為節點電壓的線性組合,求出節點電壓后,便可方便地得到各支路電壓、電流。
節點電壓在所有網孔都自動滿足KVL,因此,只需列出(n-1)個KCL方程,就可以使得電路得到求解。節點電壓法中的變量—節點電壓個數就是其余獨立節點數(n-1)個。所以節點電壓是一組獨立變量。
使用節點電壓法的工作步驟:
① 選定各節點電壓的參考方向,也就是列方程式時這個節點的電壓方向。
② 列寫(n-1)個節點的KCL方程。

其中
 稱為節點1-(n-1)的自電導,為與該節點相連的各支路的所有電導之和;
稱為節點1-(n-1)的自電導,為與該節點相連的各支路的所有電導之和;
其余電導為各個節點的互電導:計算方法是兩個相鄰節點公共支路中所有電導之和的負值,不相鄰則互電導為零)。
 為節點1-(n-1)中所有流入該節點的電源電流的代數和。注意此處,在求這個代數和時,流入為正,流出為負。
為節點1-(n-1)中所有流入該節點的電源電流的代數和。注意此處,在求這個代數和時,流入為正,流出為負。
若支路為電壓源與電阻串聯,則電流為電壓源與電阻之比,當電壓源正極性端連接該結點時取正,反之取負。
③ 聯立取求解節點電壓方程,得到節點電壓。
④ 指定待求支路電流的參考方向,根據歐姆定律就可求出該支路的電流。
下面單獨說一下,含理想電壓源支路時的求解方法:
盡可能取電壓源支路的負極性端作為參考結點。則該支路的另一端電壓為電壓源電壓,因而不必再對此節點列寫節點電壓方程;
如不能使電流源中只有一個網孔電流流過。則需要把電流源的電壓也作為變量列入網孔方程,并將電流源電流與有關網孔電流的關系作為補充方程,方程數仍然是足夠的,就可以一并求解了。
彌爾曼定理:
單結點偶電路:有兩個結點多個支路的電路。所以它只有一個獨立結點,只有一個變量,只需要列寫一個方程。
獨立節點的電壓U1的計算公式:

-
電阻電路
+關注
關注
0文章
51瀏覽量
11653 -
等效變換
+關注
關注
0文章
32瀏覽量
10721 -
等效電阻
+關注
關注
7文章
60瀏覽量
11465 -
直流電路
+關注
關注
3文章
121瀏覽量
13758 -
支路電流法
+關注
關注
0文章
18瀏覽量
6783
發布評論請先 登錄
相關推薦
變壓器直流電阻測試儀一般選多大的電流的
直流電路的過流保護設計方法
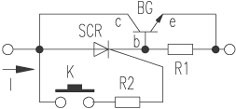




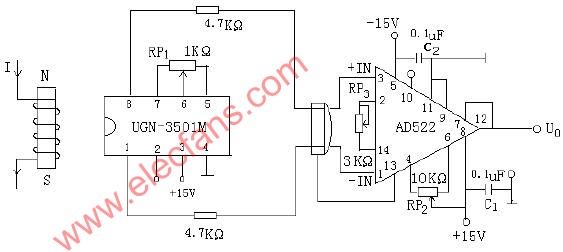
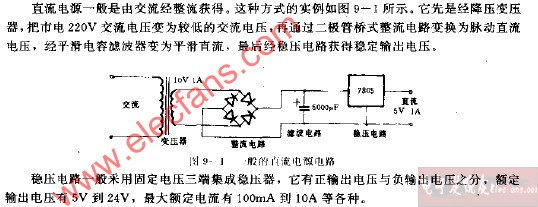
 直流電路的一般分析方法
直流電路的一般分析方法











評論