1. 說在前面的
之前調試基于QMI8658 6軸姿態解算的時候,我對Mahony濾波的認識還比較淺薄。初次的學習和代碼的移植讓我對四元數、歐拉角、旋轉余弦矩陣有了一定的接觸。然而,直到我將地磁傳感器加入到我的硬件,進行9軸姿態解算時,我深深地感受到對四元數與姿態陣之間關系的理解是非常重要的。在此之前,我檢索了網絡文章,并記錄了《MEMS_慣性傳感器09 - Mahony姿態解算算法詳解》、《MEMS_慣性傳感器14 - Mahony濾波算法的代碼分析》兩篇文章。可能對于大佬、資深工程師來說,這些文章的嚴謹性不夠,可能會誤導別人。但我必須承認,我仍然沒有扎實的數學計算研究背后更深層次的理論。即使如此,我依然希望通過自己的努力在慣性導航算法上學習得更深入一些。同時,我也想多記錄一些學到的知識,多記錄一些自己的理解和思考。希望這些記錄能幫助到一些初學者。如果我的文章有錯誤的引導,我非常希望大佬們能夠指正,因為這對我來說是最大的收獲,我非常樂意傾聽和學習。我愿意自我突圍,向著理想前進!
這次學習檢索時發現了一個博文內容硬核、有理有據的博主:路癡導航員[1]。她的博文 《AHRS互補濾波(Mahony)算法及開源代碼》對我幫助很大。
2.Mahony濾波算法的核心思想
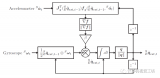
Mahony濾波算法的核心思想是通過將角速度和角度的測量值與歷史估計值進行加權平均,從而得到更加準確的姿態估計結果。同時,濾波算法還利用加速度計的測量值來糾正姿態角度的漂移。該算法也存在一些缺點,例如對于快速旋轉和加速度變化較大的情況,其姿態估計結果可能會出現較大的誤差。
3. 易懂的理解 Mahony 濾波算法的過程
為了更好的理解,表達式先不用矩陣的思想,在算法的實現的過程中,需要將表達式轉換成矩陣形式。
① 根據陀螺儀的測量數據計算出角速度的增量,即:
Δθ = 0.5 * (gyro + bias) * Δt
其中,gyro表示陀螺儀的測量值,bias表示陀螺儀的零偏誤差,Δt表示時間間隔。
② 根據加速度計的測量數據計算出重力方向的估計值,即:
g_est = q * (0, 0, -1) * q^-1
其中,q表示四元數的姿態估計值。
③ 根據加速度計的測量數據和重力方向的估計值,計算出加速度計的誤差,即:
acc_err = acc_meas - g_est
其中,acc_meas表示加速度計的測量值。
④ 根據角速度的增量和加速度計的誤差,更新四元數的姿態估計值,即:
q = q * exp(Δθ - K * acc_err)
其中,K為控制增益。
4. 其他的一些思考
傳感器EVB板的測量數據以載體坐標系(b-框架)表示。歐拉角的直觀表示描述了地理坐標系中的角度,其中包括重力的影響。地理坐標系中的重力矢量為[0,0,1]g,磁傳感器將地球磁場中的強度表示為[cos(θ),0,sin(θ)]guess。因此,在算法中,加速度和磁數據被歸一化,確保它們的模是一定大小的。
四元數從地理坐標系(東北天)轉換到載體坐標系,就得到了旋轉矩陣Cnb。
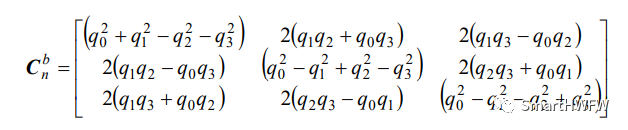
Cnb的最后一列取負,即將其轉換為載體坐標系中的值。在理想情況下,如果沒有誤差,這個矢量應該與測量值相等。然而,由于這兩者總會存在差異,因此我們需要利用它們之間的差值來修正陀螺儀更新的不準確性。
在修正的過程中,我們認為加速度計測量的可信度較高,還需要使用地磁傳感來修正加速度傳感的Z軸。磁力計的模的長度是確定的,但是兩個分量的具體大小無法像重力加速度一樣確定。因此,我們使用上一次的四元數得到的Cbn(從載體到地理坐標系的旋轉矩陣)來計算測量的磁場強度。理論上,此刻的Cbn應該在東向上的分量是零[cos(θ),0,sin(θ)],而北向和地向會有分量。然而,由于此刻的Cbn尚未得到,我們使用的是上一次的Cbn,并加上一些測量誤差,導致東向上仍會有分量存在。為了處理這種情況,我們將xy平面的分量合成到一個方向上,使得y軸上的分量為0。這樣,處理后的地磁信息的地位就與重力加速度(0,0,-1)相似了。
根據余弦矩陣和歐拉角的定義,我們可以將地理坐標系的重力向量轉換到載體坐標系中。具體而言,將四元數轉換成方向余弦矩陣后,我們可以得到方向余弦矩陣的第三列的三個元素,即vx、vy和vz。這三個元素實際上表示了當前歐拉角(即四元數)在載體坐標系上換算得到的重力單位向量。
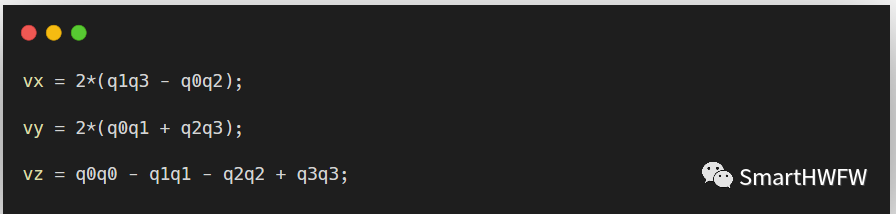
axayaz是載體坐標參照系上,加速度計測出來的重力向量。vxvyvz是陀螺積分后的姿態推算出的重力向量。它們之間的誤差向量exeyez是陀螺積分后的姿態和加計測出來的姿態之間的誤差。誤差向量可以用向量叉積來表示。叉積向量exeyez位于載體坐標系上,且其大小與陀螺積分誤差成正比,可用于糾正陀螺。由于陀螺是對機體直接積分,所以對陀螺的糾正量會直接體現在對載體坐標系的糾正。
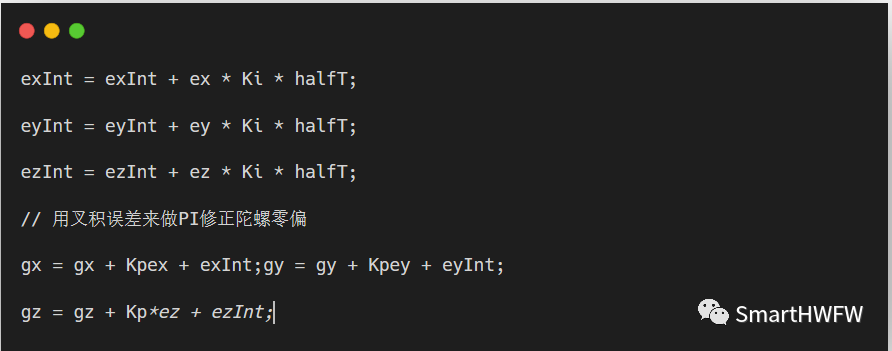
矢量之間的叉乘公式為err = A × B = |A| × |B| × sin(β)。當兩個矢量重合時,誤差為零,表示沒有差異。當兩個矢量之間夾角為90°時,誤差達到最大值,表示差異最大。然而,在夾角為90°附近的區間內,誤差的變化是非線性的,這可能導致一些準確性問題。
審核編輯:湯梓紅
-
傳感器
+關注
關注
2553文章
51392瀏覽量
756593 -
mems
+關注
關注
129文章
3958瀏覽量
191101 -
加速度計
+關注
關注
6文章
704瀏覽量
46024 -
慣性傳感器
+關注
關注
2文章
170瀏覽量
27992 -
濾波算法
+關注
關注
2文章
89瀏覽量
13776
原文標題:MEMS_慣性傳感器17-調試 Mahony 濾波算法的思考
文章出處:【微信號:SmartHWFW,微信公眾號:SmartHWFW】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
姿態融合算法是什么
介紹幾種嵌入式常用濾波算法的matlab實現
采用軟件算法實現數字濾波
基于分布式算法的FIR濾波器的設計與實現
數字圖像空域濾波算法的FPGA設計與實現
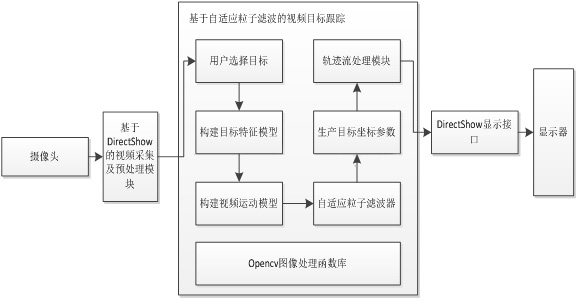
QT+Opencv粒子濾波算法實現視頻目標跟蹤——(二)濾波算法分析及測試
matlab實現的自適應濾波算法
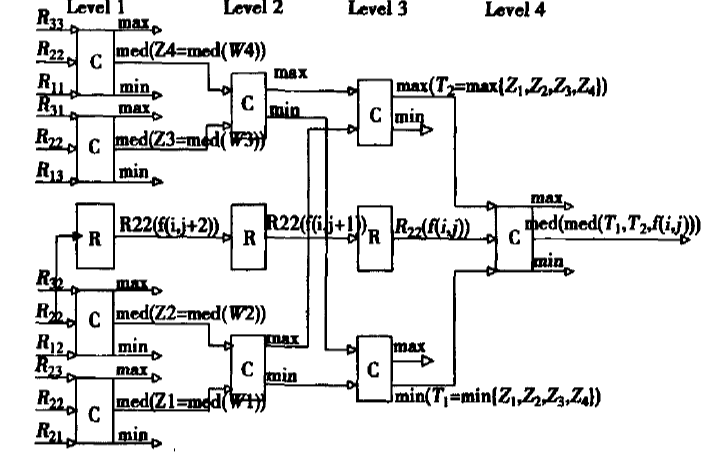
如何使用FPGA實現圖像的中值濾波算法
IMU姿態濾波算法——Mahony算法:原理與代碼

Mahony算法常見的姿態融合算法

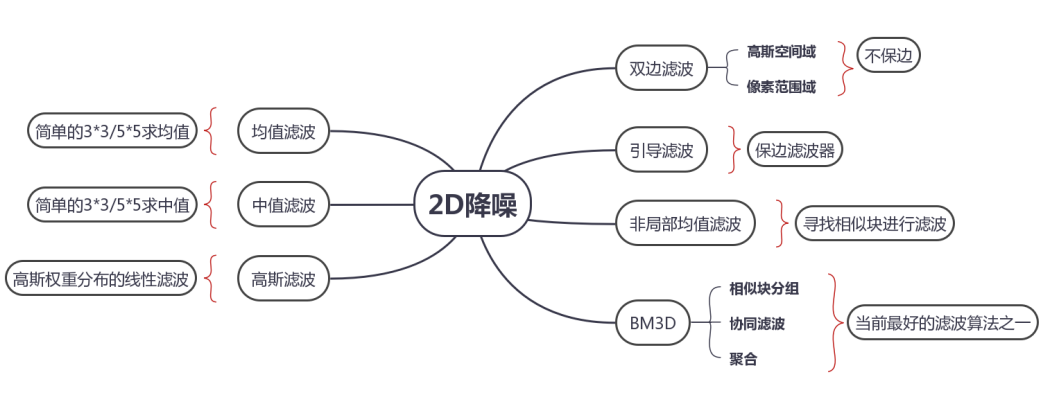
詳解從均值濾波到非局部均值濾波算法的原理及實現方式




 理解Mahony濾波算法的實現過程
理解Mahony濾波算法的實現過程










評論