由電阻很小的電感線圈組成的交流電路,都可近似地看成是純電感電路。如下圖a所示為由一個線圈構成的純電感電路。
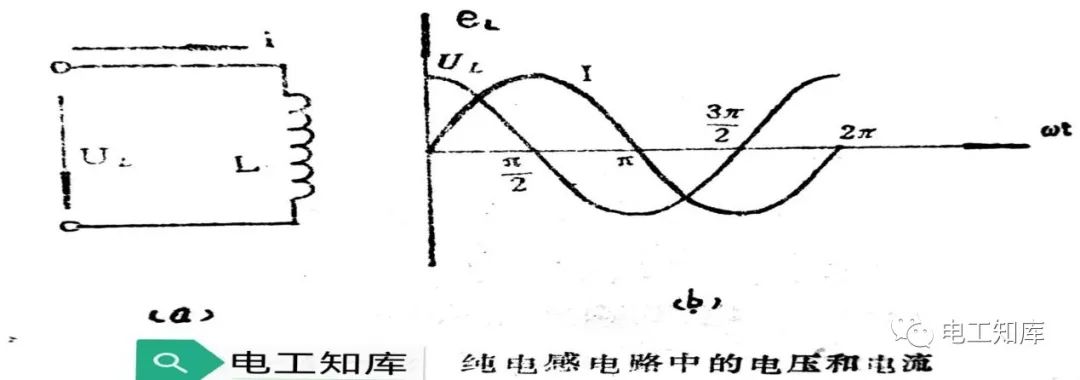
1、純電感電路中電流與電壓的相位關系
在純電感線圈的兩端,加上交流電壓u L ,線圈中必定要產生一交流電流i,由于這一電流時刻都在變化,因而線圈上就產生自感電動勢來反抗電流的改變,因而線圈中的電流變化就要落后于線圈兩端的電壓變化,uL和i之間就會有相位差。
對于一個內阻很小的電源,其電動勢與端電壓總是大小相等方向相反,因而:
u L =-e L =-(-L?i/?t)=L?i/?t
由上式可以看出,線圈兩端的電壓大小與電流的變化率成正比。下面就通過上式來分析電流與電壓之間的相位關系。
設線圈中電流的初相位為零。電流波形如上圖b所示。現把一個周期電流的變化分成四個階段來討論:
在0π/2,即第一個1/4周期內,電流從零增加到最大正值。此間電流的變化率?i/?t為正值,并且起始時最大,然后逐漸減小到零。根據uL~=L?i/?t可知,此期間的電壓uL從最大值逐漸變為零。
在π/2π,即第二個1/4周期內,電流從最大值減小到零。此間電流的變化率?i/?t為負值,并且從零變到最大負值。uL~也從零變到最大負值。
在π3π/2,即第三個1/4周期內,電流從零變為最大負值,此間電流的變化率仍為負值,且從最大負值變到零,則uL~也從最大負值變到零。
在3π/22π,即第四個1/4周期內,電流從最大負值變到零,此間電流的變化率為正值,且從零變到最大正值,則uL~也從零變到最大正值。
從以上分析可得上圖b所示的uL的波形圖。從波形圖可清楚地看出:在純電感線圈中的正弦電流要比它兩端的電壓滯后90°。即電壓總是超前電流90°。這就是純電感電路中電流和電壓的相位關系。
設流過電感的正弦電流的初相位為零,則電流、電壓的瞬時值表達式為:
i=Imsinωt
u L =ULsin(ωt+π/2)
2、純電感電路中電流與電壓的數量關系
由數學推導可知,電壓的最大值為:
U Lm =ωLIm
若把兩邊同除以√2,則得:
U L =ωLI或I=U~L~/ωL=U~L~/X~L~
式中X L =ωL=2πfL
XL稱為電感抗,簡稱感抗,它的單位是歐姆。因此,電感線圈中的電流有效值就等于線圈兩端電壓的有效值除以它的感抗。
感抗是用來表示電感線圈對交流阻礙作用的一個物理量。感抗的大小,取決于線圈的電感量L和流過它的電流頻率f。對具有某一電感量的線圈而言,f越高則XL越大。在相同電壓作用下,線圈中的電流就會減小。在直流電路中,因頻率f=0,故線圈的感抗也等于零,這時線圈只起電阻作用。由于一般線圈的電阻很小,故電感線圈可視為短路。
3、純電感電路的功率
純電感線圈的瞬時功率為:
P L =uLi
=UL~~msin(ωt+π/2)ILmsinωt
=ULmImsinωtcosωt
=ULmImsin2ωt/2
=ULIsin2ωt
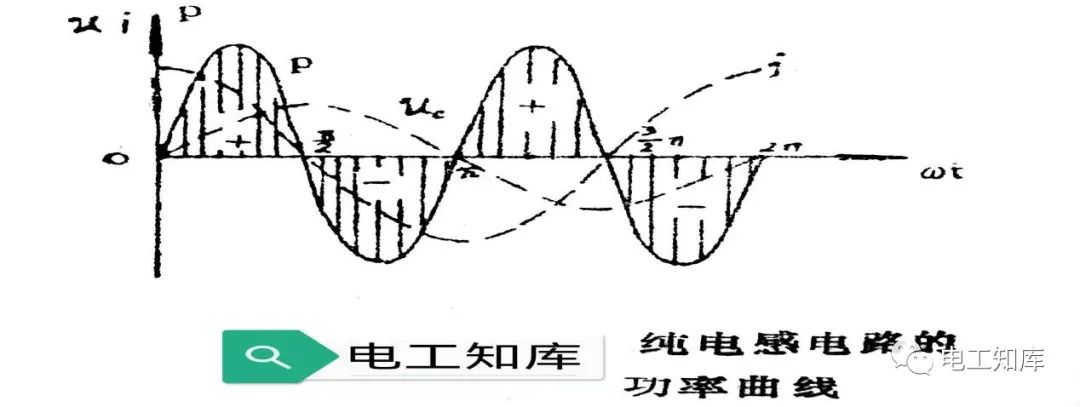
上圖畫出了PL的變化曲線,從圖中可以看到,在第一和第三個1/4周期內,PL是正值,這就表示線圈要從電源方面吸取電能并把它轉換為電磁能,儲藏在線圈周圍的磁場中,此時線圈起著一個負載的作用。但在第二和第四個1/4周期內,PL為負值,這表示線圈是向電源輸送能量。即線圖把磁能再轉換為電能而送回電源,此時線圈起著一個電源的作用。綜上所述,純電感線圈時而“吞進”功率,時而“吐出”功率,在一個周期內的平均功率為零,平均功率不能反映線圈能量交換的規模,因而就用瞬時功率的最大值來反映這種能量交換的規模,并把它叫做電路的無功功率。無功功率用字母QL表示。QL的大小為:
Q L =ULI=I^2^X~L~=U~L~^2^/X~L~
為與有功功率相區別,無功功率的單位是乏。在上式中,當各物理量的單位分別用伏特、安培、歐姆時,無功功率的單位是乏(var)。
必須指出,“無功”的含義是“交換”而不是“消耗”,它是相對“有功”而言的,絕不能理解為“無用”。
-
電流
+關注
關注
40文章
6941瀏覽量
132682 -
電壓
+關注
關注
45文章
5637瀏覽量
116255 -
純電感電路
+關注
關注
0文章
5瀏覽量
3868
發布評論請先 登錄
相關推薦




 純電感電路中電流與電壓的相位關系
純電感電路中電流與電壓的相位關系
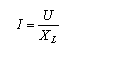










評論