1. 引言
有鑒于數字信號處理涉及的面太多,我們必須要把話題收縮。數字濾波的種類也是五花八門,因此再選一個小的類型,我們將圍繞離散線性時不變系統(Discrete Linear Time-Invariant System)來簡單討論一下陷波濾波器(Notch Filter)和梳狀濾波器(Comb Filter),通過代碼的演示和輸出,我們可以比較一下這兩類濾波器的特點。在本文中我們先以陷波濾波器為題來討論相關的內容。
關于濾波,我們多少會了解一些,諸如帶通,帶阻,高通,低通等特性。信號濾波,其實我們在很多的應用中都會不自覺地應用起來,比如ADC值的多次采樣平均——這是一種典型的數字濾波方式,當然也是最簡單濾波方式中的一種。
2. 關于線性移不變系統和數字濾波器
何謂線性移不變系統?主要是兩點:
系統的弛豫狀態滿足可疊加原理(表現為線性,比例性)
系統的弛豫狀態時移不變,即任意時間平移量k,有x(n-k)→T→ y(n-k) )
再加上系統是因果的(如果一個系統的輸出僅僅依賴于過去和現在的輸入,而不依賴于未來的輸入,那么此系統就被稱為因果系統),穩定的(系統輸出不是發散振蕩的),就構成我們濾波器的幾個基本要素。
一個弛豫的系統是指當初始時刻系統內部無能量或所有狀態變量的初值為零的系統,也就是說該系統的所有狀態變量都已經"弛豫"到它們的穩定或靜態值。在弛豫條件下,系統中不存在任何內部能量或動力以推動系統產生輸出。換句話說,所有的輸出都將僅被輸入驅動。
在差分方程或差分方程系統中,所謂的"初始條件為零"或"弛豫的初始條件",意味著所有的y(n)(對于n<0)都被假定為零,即系統在開始接收輸入(即n=0)之前是"靜止"或"弛豫"的。對于許多系統和信號處理分析,完全弛豫的假設能夠簡化計算和分析過程。然而,實際上,實際的物理系統可能需要一些時間才能達到完全弛豫的狀態。
離散數字濾波器在時域上可以用常系數差分方程來表示:
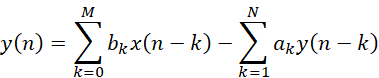
(1)
其中ak,bk都是已知常數,但是該方程中,并不能直接看到y(n)和x(n)之間的等式關系,實際應用最好通過軟件迭代的方式才方便處理。我們以參考書本[1]上的例子簡單說明。假如一個遞歸的輸入輸出方程有:
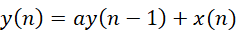
設定對n<0的輸入信號不計,輸出部分只考慮y(-1),那么省掉遞推過程,可以得到:
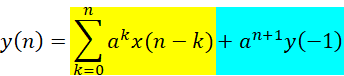
,其中n>0
y(n)的結果表達式中,第一部分是系統的零輸入響應,第二部分是零狀態響應(顏色區分)。如果該系統的初始狀態是弛豫的,即有:
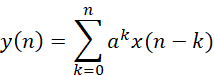
關于系統的線性,從上式可以知道,對于系統S和任意輸入x1,x2和常數c1,c2,有如下等式說明當前系統是滿足疊加性的,因此系統是線性的。
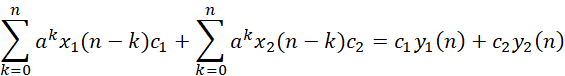
其中關于兩個響應的說明:
零狀態響應(ZSR):這是指當系統的初始狀態為零,即沒有存儲的能量和信息,對系統的新輸入信號產生的響應。這個響應完全由當前的輸入驅動,和系統在初始時刻的狀態無關。ZSR是系統特性(如系統函數、沖激響應等)和輸入信號的函數。
零輸入響應(ZIR):這是指當系統的輸入為零,即沒有新輸入信號,系統由其初始狀態或初始條件產生的響應。這通常描述了系統如何在沒有外部輸入的情況下,自然地演化和衰減,即系統的自由響應。ZIR僅僅取決于系統的特性和初始狀態
上面的結論是通過簡單的時域例子來說明的,可能無法代表全狀態的方程。我們通過對式-1單邊Z變換的方式從復頻域的角度來加深理解一下(將Z=e^jω帶入,就轉入頻域)。單邊Z變換中,輸入信號x(n)被認為是因果的,因此不考慮x(n),n<0的輸入,并且以前的輸入所有信號的作用都反映在初始條件y(-1),y(-2),…,y(-N)上。將式-1經過單邊Z變換,我們可以得到[1]:
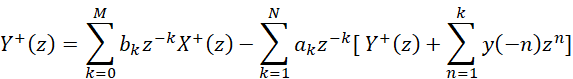
(2)
式-2經過合并可得(式-3):

(3)
式-3中,前半部分就是系統的零狀態響應;后半部分就是零輸入響應,和系統以前的狀態相關。系統的響應組成和在時域的響應組成是相同的。而且我們也知道,復頻域中,下面的系統等式也是屬于LTI的:
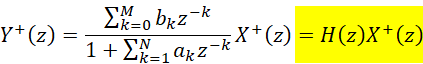
(4)
對于一般性的我們有:
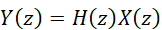
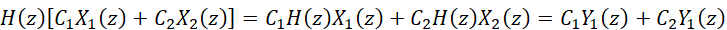 ????(5)
????(5)
式-5所表達的系統在復頻域的弛豫狀態,是滿足疊加性要求的,因此系統是線性的。
我們再看關于系統符合線性系統的其他要求:
總響應等于零輸入響應和零狀態響應之和;
零狀態響應滿足疊加法則;
零輸入響應滿足疊加法則。
關于系統時移,我們知道,在時域的時移,對應復頻域中在z平面上的旋轉:
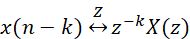
如果將z=e^jω代入,就可以將式-4轉換到頻域的輸入到輸出的頻幅響應。我們有:
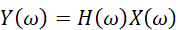
此時如果輸入信號有時移x(n-k),我們得到的系統響應將是:
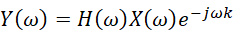
這種情況下,無論e^(-jωk)是系統的頻率響應H(ω)引起的相應變化,還是輸入信號X(ω)本身的時延引起的相位變化,效果是一樣的。另外,如果頻率響應H(ω)對輸入信號的幅度有同樣的縮放功能|H(ω)|。這些對于信號本身可以不認為是失真的。
事實上,線性時不變系統和濾波器這兩個術語是同義的。某種意義上,H(ω)對于輸入信號中不同的頻率成分起著加權函數或頻譜整形函數的作用[1]。這就是我們圍繞系統函數H(ω)展開如何設計濾波器的由來。
既然這里又回到了濾波器這個話題,我們再將內容收縮一下,從陷波濾波器開始。式-1中,如果任意a_k=0,那么這個系統屬于有限沖激響應系統(FIR);有任意a_k≠0,就會被稱之為無限沖擊響應系統(IIR)。
3. 陷波濾波器(Notch Filter)
陷波濾波器,也稱為陷帶濾波器,是一種在某一特定頻率或者頻率范圍上,將信號的幅度衰減到極低甚至為零的濾波器。它屬于帶阻濾波器的特例,帶阻濾波器是一種抑制某一頻帶內的信號而允許頻帶以外的信號通過的濾波器。它們的區別在于陷波濾波器的阻止帶寬通常更窄,目標更準確。如果是針對某個單一頻率的信號進行濾波,那么該濾波器的品質因數Q值的要求也會更高,以便讓被阻止的帶寬足夠窄而不影響該頻率附件信號的傳遞。但是過高的Q值就可能會引起濾波器的抖動,這個我們在設計濾波器的過程中,是需要留意的。
陷波濾波器的特性:
目標頻率或頻道的信號被顯著削弱,而其他頻率的信號幾乎不受影響。
陷波頻率或頻帶的選擇往往能夠調整。
能有效削弱或消除特定頻率的噪聲或干擾。
應用場合:
音頻處理:在音樂制作或音頻修復中,陷波濾波器用于消除特定的干擾音,例如電流電壓的噪聲。
工業現場信號采集處理系統:比如用于濾除50或60Hz的工頻噪聲。
通信系統:超窄帶陷波濾波器用于從廣帶信號中選擇性地濾除某一特定信號。
醫療和生物工程:用于消除生物和醫療信號中的電源頻率以及任何周期性干擾。
雷達和導航系統:從信號中移除某一特定頻率的干擾。
陷波濾波器為了更準確抑制特定頻段的信號而設計,因此相比普通帶阻濾波器,它的阻帶通常會設置得更窄更精確。
我們通過模擬信號以及濾波處理后的信號之間進行對比,來了解這種類型濾波器的特點。
模擬信號中有50Hz的工頻干擾信號需要濾除,保留20Hz的有用信號。先看結果,后查代碼[2](在本文的最后部分)。
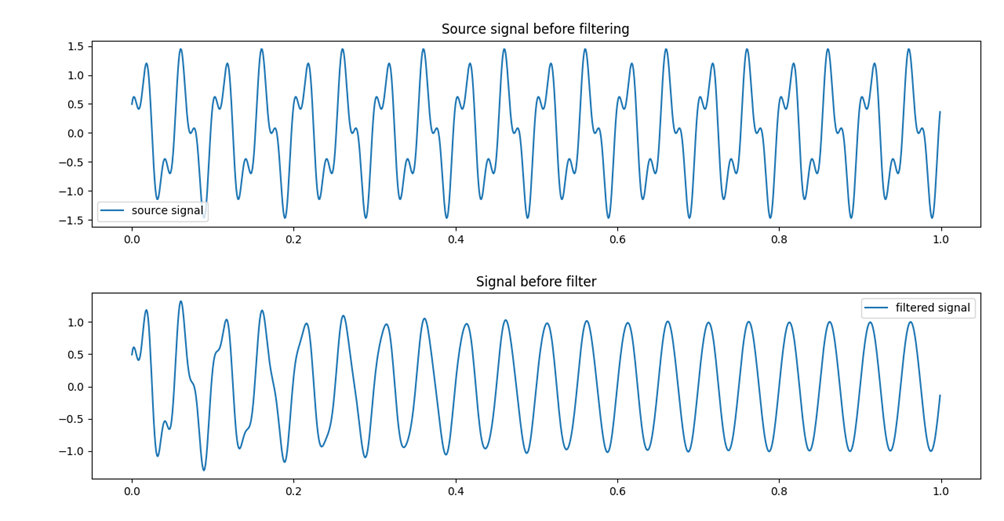
圖-1 信號濾波前后對比
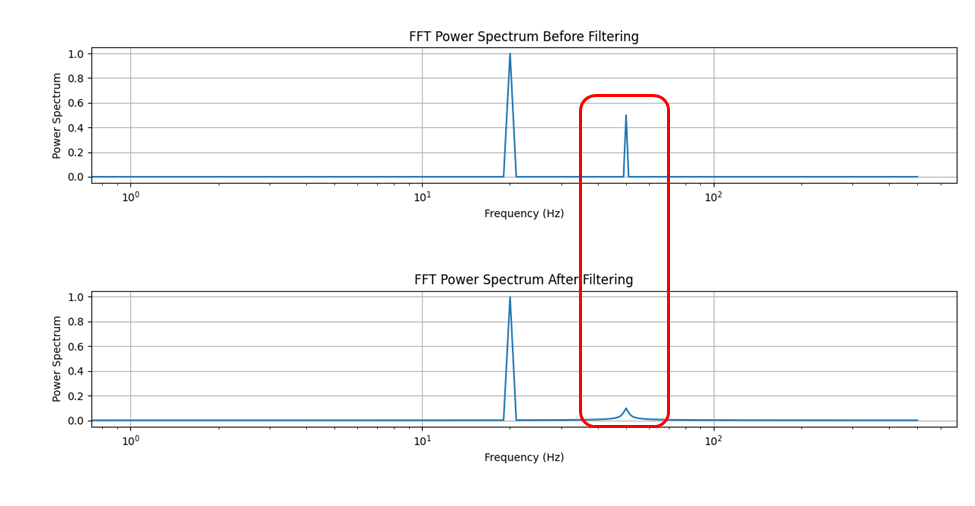
圖-2 信號濾波前后的頻譜圖(削弱后的50Hz信號)
第三個圖,是我們陷波濾波器典型的特征圖。在指定的頻率處對輸入信號進行衰減,而其他頻率處保持通過。
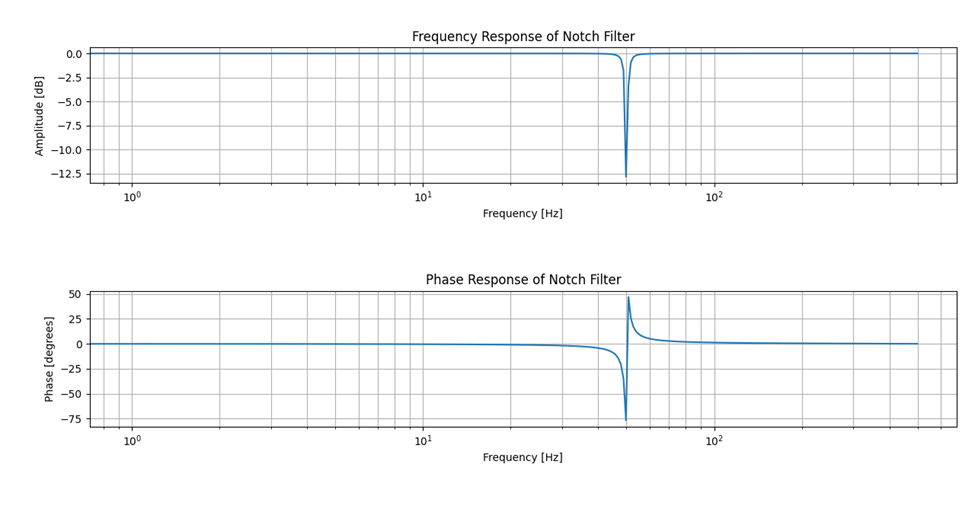
圖-3 濾波器的幅相頻響應圖
該2階IIR濾波器在50Hz之外的頻域的信號都可以保持的通過性。參數如下(程序中有輸出):
b0~b2: [ 0.99479124, -1.89220538, 0.99479124]
a0~a2: [ 1.0 , -1.89220538, 0.98958248]
對應的系統函數有:
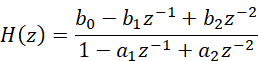
(6)
陷波濾波器對于特定的頻率過濾有其獨到的用途。該模擬測試程序可以在本文的附頁部分查看。通過計算得到系統函數在z平面中對應的零點和極點結果如下(本文最后提供計算代碼):
| 零點1 | 零點2=零點1* | |
| 結果 | 0.9510565151337682+0.3090169979493239j | 0.9510565151337682-0.3090169979493239j |
| 絕對值 | 1.0 | 1.0 |
| 相角 | 18.00000021533598° | -18.00000021533598° |
| 極點1 | 極點2=極點1* | |
| 結果 | 0.94610269+0.3073632703736149j | 0.94610269-0.3073632703736149j |
| 絕對值 | 0.9947776032862823 | 0.9947776032862823 |
| 相角 | 17.997582759707843° | -17.997582759707843° |
在設計二階Notch濾波器時,零點和極點的位置和數值對濾波器的性能起著關鍵的作用。在上面的模擬的濾波器中,z平面中的2個零點就在單位圓上,不過兩個極點已經很靠近單位圓了,實際應用中需要進一步測試驗證以避免濾波器的額外抖動。
大家可以嘗試用C/C++的方式將參數轉換為代碼,成為你所需的濾波器。這里使用的是Python中的IIR方式,而如果真要用FIR方式實現同樣的效果,通常會需要很高的濾波器階次,反而會導致計算復雜度增加,響應也會滯后。以下是設計陷波濾波器的一些基本的要求:
零點的位置:Notch濾波器的零點通常被放在單位圓上,其位置決定了阻止頻率的相關位置。要阻止的頻率就是零點所在的角度對應的頻率。
極點的位置:極點的位置靠近零點可以產生較窄的Notch帶寬,這意味著濾波器能夠拒絕的頻率范圍較窄。相反,如果極點離零點較遠,那么Notch帶寬將較寬。但需要注意的是,極點的位置必須在單位圓內,否則濾波器將不穩定。
零點和極點的數值:這些數值決定了濾波器的具體阻止頻率和帶寬。通過精確地選擇這些數值,可以設計出滿足各種應用要求的濾波器。
總的來說,設計Notch濾波器時,需要根據具體的阻止頻率和帶寬需求,精確地調整零點和極點的位置和數值。并且要確保極點的位置在單位圓內,以保證濾波器的穩定。具體數值的確定可以借助各種濾波器設計工具進行計算。
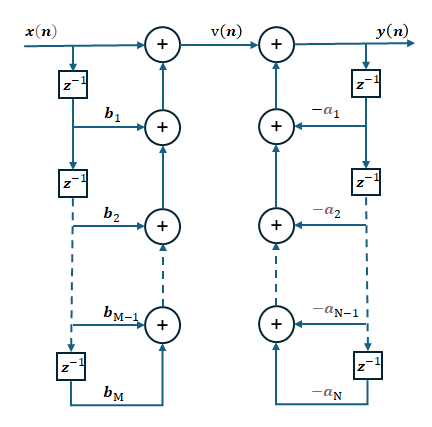
圖-4 濾波器的信號傳遞
4. 小結
在本文中,我們詳細探討了Notch濾波器的設計和應用。我們理解了Notch濾波器的工作原理以及如何有效消除特定頻率的干擾。此外,我們還簡單了解了如何根據需求對濾波器進行設計,特別是零點和極點的定位。
通過理解和正確應用這些原則,我們可以設計出性能優秀的Notch濾波器,這對于許多應用場景,如信號處理,噪聲消除等領域都是非常重要的。在很多工業現場的傳感器應用中,會涉及很多信號的相對高速采集的場合,會用到Notch濾波器,尤其針對諸如工頻干擾,或者特定頻率的過濾等。
安費諾傳感器(Amphenol Sensors)提供諸多滿足您應用的可靠、準確高精度的傳感器,但如果實際應用過程中碰到一些異常的信號,可以和我們一起來分析原因,解決問題,根據實際工況來改善應用。
后續的文檔中,我們將簡單討論另一種濾波器——梳狀濾波器(Comb Filter),并通過Python模擬該濾波器的功能和實現,以及一些特情的處理方式。
陷波濾波器模擬測試Python代碼
import numpy as np import matplotlib.pyplot as plt from scipy import signal from scipy import fft,fftpack # 采樣頻率 fs = 1000 # 設計帶阻濾波器,過濾50Hz噪聲 f0 = 50.0 # Frequency to be removed from signal (Hz) Q = 30.0 # Quality factor w0 = f0/(fs/2) # 設計歸一化頻率 b, a = signal.iirnotch(w0, Q) # 生成一段帶噪音的信號 t = np.arange(0, 1.0, 1/fs) # Time vector x = np.sin(2*np.pi*20*t) # 20Hz sine wave x = x + 0.5*np.cos(2*np.pi*f0*t + .1) # 50Hz sine wave # 設計濾波器并應用 yi = signal.lfilter(b, a, x) # 輸出該濾波器的參數 print("Filter Parameters:","b:",b,"a:",a) # 繪制信號的波形圖 plt.figure(1) plt.subplot(211) plt.title('Source signal before filtering') plt.plot(t, x, label='source signal') plt.legend() # 繪制信號的頻譜圖 plt.subplot(212) plt.title('Signal before filter') plt.plot(t, yi, label='filtered signal') plt.legend() plt.tight_layout() plt.show() # 進行FFT變換 xf = np.linspace(0.0, 1.0/(2.0/fs), fs//2) signal_original = fftpack.fft(x) # 源信號的FFT signal_filtered = fftpack.fft(yi) # 濾波之后的FFT # 繪制信號的FFT圖 plt.figure(figsize=(8, 4)) plt.subplot(2, 1, 1) plt.semilogx(xf, 2.0/len(x) * np.abs(signal_original[0:len(x)//2]), label='source signal') plt.title('FFT Power Spectrum Before Filtering') plt.xlabel('Frequency (Hz)') plt.ylabel('Power Spectrum') plt.grid() plt.subplot(2, 1, 2) plt.semilogx(xf, 2.0/len(signal_filtered) * np.abs(signal_filtered[0:len(signal_filtered)//2]), label='filtered signal') plt.title('FFT Power Spectrum After Filtering') plt.xlabel('Frequency (Hz)') plt.ylabel('Power Spectrum') plt.grid() plt.tight_layout() plt.show() # 繪濾波器的幅度頻響應和相頻響應 freq, h = signal.freqz(b, a, fs=fs) plt.figure(figsize=(8, 4)) plt.subplot(2, 1, 1) plt.semilogx(freq, 20*np.log10(abs(h))) plt.title('Frequency Response of Notch Filter') plt.xlabel('Frequency [Hz]') plt.ylabel('Amplitude [dB]') plt.grid(which='both', axis='both') angle = np.unwrap(np.angle(h)) plt.subplot(2, 1, 2) plt.semilogx(freq, angle * 180 / np.pi) plt.title('Phase Response of Notch Filter') plt.xlabel('Frequency [Hz]') plt.ylabel('Phase [degrees]') plt.grid(which='both', axis='both') plt.tight_layout() plt.show()
通過濾波器的參數計算濾波器Z平面的零、極點(Zero/Pole)的Python
import cmath
import math
# 定義系數
b = [0.99479124, -1.89220538, 0.99479124] # 用新的參數替換掉表中的
a = [1.0, -1.89220538, 0.98958248]
# 計算0點
zero1 = (- b[1] + cmath.sqrt(b[1]**2 - 4 * b[0] * b[2])) / (2 * b[0])
zero2 = (- b[1] - cmath.sqrt(b[1]**2 - 4 * b[0] * b[2])) / (2 * b[0])
# 計算極點
pole1 = (- a[1] + cmath.sqrt(a[1]**2 - 4 * a[0] * a[2])) / (2 * a[0])
pole2 = (- a[1] - cmath.sqrt(a[1]**2 - 4 * a[0] * a[2])) / (2 * a[0])
# 計算相位角
zero1_abs = abs(zero1)
zero2_abs = abs(zero2)
pole1_abs = abs(pole1)
pole2_abs = abs(pole2)
zero1_angle = cmath.phase(zero1)
zero2_angle = cmath.phase(zero2)
pole1_angle = cmath.phase(pole1)
pole2_angle = cmath.phase(pole2)
phase_degrees_zero1 = math.degrees(zero1_angle)
phase_degrees_zero2 = math.degrees(zero2_angle)
phase_degrees_pole1 = math.degrees(pole1_angle)
phase_degrees_pole2 = math.degrees(pole2_angle)
print("Zeros: ", zero1, zero2)
print("Poles: ", pole1, pole2)
print("Zeros Angles: ", zero1_angle, zero2_angle, "abs Zeros:", zero1_abs, zero2_abs)
print("Poles Angles: ", pole1_angle, pole2_angle, "abs Poles:", pole1_abs, pole2_abs)
print("零點相位的度數為:", phase_degrees_zero1,phase_degrees_zero2)
print("極點相位的度數為:", phase_degrees_pole1,phase_degrees_pole2)
-
adc
+關注
關注
99文章
6533瀏覽量
545755 -
數字濾波器
+關注
關注
4文章
270瀏覽量
47095 -
陷波濾波器
+關注
關注
2文章
33瀏覽量
10084
原文標題:數字濾波器(1)——陷波濾波器
文章出處:【微信號:安費諾傳感器學堂,微信公眾號:安費諾傳感器學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




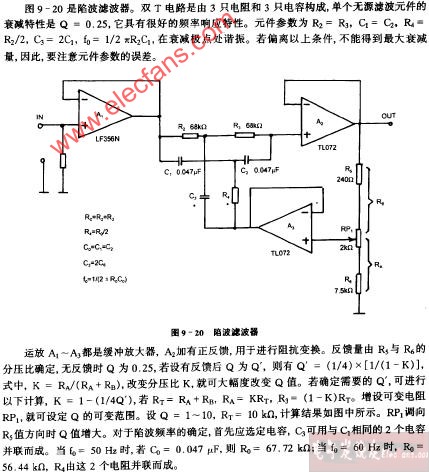
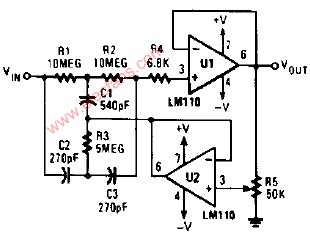
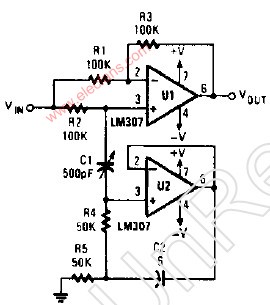
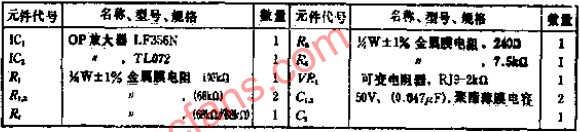
 陷波濾波器的相關知識
陷波濾波器的相關知識










評論