一、引言

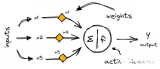
在神經網絡中，激活函數是一個至關重要的組成部分，它決定了神經元對于輸入信號的反應方式，為神經網絡引入了非線性因素，使得網絡能夠學習和處理復雜的模式。本文將詳細介紹神經網絡中常用的激活函數，包括其定義、特點、數學形式以及在神經網絡中的作用和用途。

二、常用的激活函數

Sigmoid函數

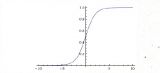
Sigmoid函數是一種常用的S型激活函數，它將輸入的實數映射到(0,1)之間。數學形式為：f(x) = 1 / (1 + e^(-x))。

優點：輸出范圍在(0,1)之間，可以表示概率；具有平滑的S形曲線，可以保持梯度的連續性，有利于反向傳播算法的穩定性。

缺點：當輸入較大或較小時，梯度會接近于零，導致梯度消失問題；輸出不是以零為中心，可能導致梯度更新不均勻，影響訓練速度。

Tanh函數（雙曲正切函數）

Tanh函數也是一種S型激活函數，將輸入的實數映射到(-1,1)之間。數學形式為：f(x) = (ex - e(-x)) / (ex + e(-x))。

優點：輸出范圍在(-1,1)之間，相比Sigmoid函數更廣泛，可以提供更大的梯度，有利于神經網絡的學習；是Sigmoid函數的平移和縮放版本，具有相似的S形曲線，但輸出以零為中心，有助于減少梯度更新不均勻的問題。

缺點：在極端輸入值時，梯度仍然會變得非常小，導致梯度消失的問題。

ReLU函數（Rectified Linear Unit，修正線性單元）

ReLU函數是一種簡單而有效的激活函數，它將輸入的實數映射到大于等于零的范圍。數學形式為：f(x) = max(0, x)。

優點：在實踐中，ReLU函數比Sigmoid和Tanh函數更快地收斂；當輸入為正時，ReLU函數的梯度為常數，避免了梯度消失的問題；計算簡單，只需比較輸入和零的大小即可，運算速度快。

缺點：當輸入為負時，ReLU函數的梯度為0，這被稱為“神經元死亡”現象，可能導致一些神經元永遠不會被激活，影響模型的表達能力；ReLU函數輸出不包括負值，這可能會導致一些神經元的輸出偏向于0。

Leaky ReLU函數

Leaky ReLU函數是對ReLU函數的改進，它解決了ReLU函數在負數部分輸出為零的問題。數學形式為：f(x) = max(αx, x)，其中α是一個小的正數（如0.01）。

優點：Leaky ReLU函數解決了ReLU函數的“死亡”現象，使得神經元可以在輸入為負時被激活；保留了ReLU函數的快速計算速度。

缺點：需要額外的超參數α，這增加了模型的復雜性；當α設置不當時，Leaky ReLU函數可能會導致神經元輸出過大或過小，影響模型的表達能力。

ELU函數（Exponential Linear Unit，指數線性單元）

ELU函數也是ReLU函數的一種改進形式，它在負數部分采用指數函數來避免“死亡”現象。數學形式為：f(x) = x（如果x > 0），α(e^x - 1)（如果x ≤ 0），其中α是一個超參數。

優點：解決了ReLU函數的“死亡”現象；當輸入為負時，ELU函數具有負飽和度，這有助于提高模型的魯棒性；ELU函數的輸出可以被歸一化，這有助于模型的訓練。

缺點：需要計算指數函數，這可能會增加模型的計算復雜度；當輸入為正時，ELU函數的梯度仍然可能變得非常小，導致梯度消失的問題。

Softmax函數

Softmax函數通常用于多分類問題的輸出層，它將神經網絡的原始輸出轉換為概率分布。數學形式為：f(x)_i = e^(x_i) / Σ_j e^(x_j)，其中x_i表示第i個神經元的輸出，Σ_j e^(x_j)表示所有神經元輸出的指數和。

優點：可以將輸出映射到概率空間，適用于分類問題；在多分類問題中表現良好。

缺點：可能會導致梯度消失或梯度爆炸的問題；計算復雜度較高，特別是在輸出維度較大時。

三、總結

激活函數在神經網絡中扮演著重要的角色，它們為神經網絡引入了非線性因素，使得網絡能夠學習和處理復雜的模式。不同的激活函數具有不同的特點和優缺點，適用于不同的任務和數據集。在選擇激活函數時，需要根據具體的應用場景和需求進行權衡和選擇。同時，隨著深度學習技術的不斷發展，新的激活函數也不斷被提出和應用，為神經網絡的優化和改進提供了新的思路和方法