神經網絡是一種強大的機器學習模型,廣泛應用于各種領域,如圖像識別、語音識別、自然語言處理等。神經網絡的核心是前向傳播和反向傳播算法。本文將詳細介紹神經網絡的前向傳播和反向傳播的區別,以及它們在神經網絡訓練中的作用。
- 前向傳播(Forward Propagation)
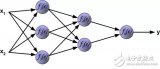
前向傳播是神經網絡中最基本的過程,它將輸入數據通過網絡層進行逐層計算,最終得到輸出結果。前向傳播的過程可以分為以下幾個步驟:
1.1 初始化輸入數據
在神經網絡的輸入層,我們將輸入數據初始化為網絡的輸入。輸入數據可以是圖像、音頻、文本等多種形式,它們需要被轉換為數值型數據,以便神經網絡進行處理。
1.2 激活函數
激活函數是神經網絡中的關鍵組成部分,它為網絡引入非線性,使得網絡能夠學習復雜的函數映射。常見的激活函數有Sigmoid、Tanh、ReLU等。激活函數的作用是對輸入數據進行非線性變換,增加網絡的表達能力。
1.3 權重和偏置
權重和偏置是神經網絡中的參數,它們在訓練過程中不斷更新,以優化網絡的性能。權重決定了輸入數據在網絡中的權重,而偏置則為網絡提供了一個偏移量,使得網絡能夠更好地擬合數據。
1.4 矩陣運算
在神經網絡中,每一層的輸出都是通過矩陣運算得到的。矩陣運算包括加權求和和激活函數的計算。加權求和是將輸入數據與權重相乘,然后加上偏置,得到當前層的輸出。激活函數則對加權求和的結果進行非線性變換,得到最終的輸出。
1.5 逐層傳遞
神經網絡通常由多個隱藏層組成,每個隱藏層都會對輸入數據進行處理。前向傳播的過程就是將輸入數據逐層傳遞,直到最后一層得到輸出結果。
- 反向傳播(Backpropagation)
反向傳播是神經網絡訓練中的關鍵算法,它通過計算損失函數的梯度,更新網絡的權重和偏置,以優化網絡的性能。反向傳播的過程可以分為以下幾個步驟:
2.1 損失函數
損失函數是衡量神經網絡性能的指標,它衡量了網絡輸出與真實標簽之間的差異。常見的損失函數有均方誤差(MSE)、交叉熵(Cross-Entropy)等。損失函數的選擇取決于具體的任務和數據類型。
2.2 計算梯度
在反向傳播中,我們需要計算損失函數關于權重和偏置的梯度。梯度是一個向量,它指示了損失函數在當前點的增長方向。通過計算梯度,我們可以知道如何調整權重和偏置,以減小損失函數的值。
2.3 鏈式法則
在神經網絡中,由于存在多個層和激活函數,我們需要使用鏈式法則來計算梯度。鏈式法則是一種數學方法,它允許我們通過計算復合函數的導數,來得到每個單獨函數的導數。在神經網絡中,鏈式法則用于計算損失函數關于每個權重和偏置的梯度。
2.4 更新權重和偏置
根據計算得到的梯度,我們可以使用梯度下降算法來更新網絡的權重和偏置。梯度下降算法的核心思想是沿著梯度的反方向更新參數,以減小損失函數的值。更新的幅度由學習率決定,學習率是一個超參數,需要根據具體任務進行調整。
2.5 迭代優化
神經網絡的訓練是一個迭代優化的過程。在每次迭代中,我們都會進行前向傳播和反向傳播,計算損失函數的梯度,并更新權重和偏置。通過多次迭代,網絡的性能會逐漸提高,直到達到滿意的效果。
- 前向傳播與反向傳播的區別
前向傳播和反向傳播是神經網絡中兩個不同的過程,它們在網絡訓練中扮演著不同的角色。以下是它們之間的主要區別:
3.1 目的不同
前向傳播的目的是將輸入數據通過網絡層進行計算,得到輸出結果。而反向傳播的目的是計算損失函數的梯度,更新網絡的權重和偏置,以優化網絡的性能。
3.2 過程不同
前向傳播是一個自上而下的過程,從輸入層開始,逐層傳遞到輸出層。而反向傳播是一個自下而上的過程,從輸出層開始,逐層傳遞到輸入層。
3.3 參數更新
在前向傳播中,網絡的權重和偏置是固定的,不會發生變化。而在反向傳播中,我們會根據計算得到的梯度更新網絡的權重和偏置。
3.4 依賴關系
前向傳播是反向傳播的基礎,反向傳播需要前向傳播的結果作為輸入。在每次迭代中,我們都會先進行前向傳播,然后進行反向傳播。
-
神經網絡
+關注
關注
42文章
4779瀏覽量
101168 -
數據
+關注
關注
8文章
7139瀏覽量
89576 -
圖像識別
+關注
關注
9文章
521瀏覽量
38386 -
機器學習模型
+關注
關注
0文章
9瀏覽量
2607
發布評論請先 登錄
相關推薦
解讀多層神經網絡反向傳播原理




 神經網絡前向傳播和反向傳播區別
神經網絡前向傳播和反向傳播區別
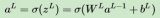











評論