時序邏輯電路是數字電路中的一種重要類型,它具有存儲功能,能夠根據輸入信號和內部狀態的變化來改變其輸出。時序邏輯電路廣泛應用于計算機、通信、控制等領域。本文將介紹時序邏輯電路的描述方法,包括狀態圖、狀態表、有限狀態機、卡諾圖、布爾差分方程、布爾函數、時序邏輯仿真等。
- 狀態圖
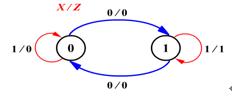
狀態圖是一種圖形化的描述方法,用于表示時序邏輯電路的狀態轉換關系。狀態圖由節點和有向邊組成,節點表示電路的狀態,有向邊表示狀態之間的轉換。狀態圖的繪制步驟如下:
1.1 確定狀態集合:首先需要確定電路的所有可能狀態,并將它們表示為狀態集合。
1.2 確定初始狀態:在狀態集中選擇一個狀態作為初始狀態。
1.3 確定輸入變量:確定電路的輸入變量,它們將影響狀態轉換。
1.4 繪制狀態轉換:根據電路的邏輯功能,繪制狀態之間的轉換關系。對于每個狀態,列出所有可能的輸入變量組合,并確定它們對應的下一個狀態。
1.5 標注狀態轉換條件:在有向邊旁邊標注狀態轉換的條件,通常使用布爾表達式表示。
1.6 檢查狀態圖的完整性:確保狀態圖包含了所有可能的狀態轉換。
- 狀態表
狀態表是一種表格化的描述方法,用于表示時序邏輯電路的狀態轉換關系。狀態表通常包括以下幾列:當前狀態、輸入變量、輸出變量和下一個狀態。狀態表的編制步驟如下:
2.1 確定狀態集合:與狀態圖相同,首先確定電路的所有可能狀態。
2.2 列出輸入變量:確定電路的輸入變量,并在狀態表的左側列出它們。
2.3 列出輸出變量:確定電路的輸出變量,并在狀態表的右側列出它們。
2.4 填充狀態表:對于每個狀態和輸入變量的組合,確定下一個狀態和輸出變量,并將它們填入狀態表中。
2.5 檢查狀態表的完整性:確保狀態表包含了所有可能的狀態轉換。
- 有限狀態機(FSM)
有限狀態機是一種抽象的計算模型,用于描述時序邏輯電路的狀態轉換關系。有限狀態機由一組狀態、一組輸入變量、一組輸出變量和一組狀態轉換規則組成。有限狀態機的描述方法包括:
3.1 確定狀態集合:與狀態圖和狀態表相同,首先確定電路的所有可能狀態。
3.2 確定初始狀態:在狀態集中選擇一個狀態作為初始狀態。
3.3 確定輸入變量:確定電路的輸入變量,它們將影響狀態轉換。
3.4 確定輸出變量:確定電路的輸出變量,它們將根據狀態轉換結果產生。
3.5 確定狀態轉換規則:根據電路的邏輯功能,確定狀態轉換規則。狀態轉換規則通常使用布爾表達式表示。
3.6 描述有限狀態機:使用狀態圖或狀態表描述有限狀態機的狀態轉換關系。
- 卡諾圖
卡諾圖是一種圖形化的優化方法,用于簡化布爾函數。卡諾圖的繪制步驟如下:
4.1 列出布爾函數的真值表:首先列出布爾函數的所有可能輸入組合及其對應的輸出值。
4.2 繪制卡諾圖:根據輸入變量的數量,繪制相應大小的卡諾圖。卡諾圖由單元格組成,每個單元格對應一個輸入組合。
4.3 標記1值:在卡諾圖中,將真值表中的1值對應的單元格標記出來。
4.4 尋找覆蓋1值的最小集合:在卡諾圖中,尋找能夠覆蓋所有1值的最小單元格集合。這些單元格集合可以共享邊或頂點。
4.5 簡化布爾函數:使用找到的最小單元格集合,構造簡化后的布爾函數。
- 布爾差分方程
布爾差分方程是一種代數化的描述方法,用于表示時序邏輯電路的狀態轉換關系。布爾差分方程的建立步驟如下:
5.1 確定狀態變量:首先確定電路的狀態變量,它們將表示電路的狀態。
5.2 確定輸入變量:確定電路的輸入變量,它們將影響狀態轉換。
5.3 建立狀態方程:根據電路的邏輯功能,建立狀態變量與輸入變量之間的關系,通常使用布爾表達式表示。
5.4 建立輸出方程:根據狀態變量和輸入變量,建立輸出變量與它們之間的關系,通常使用布爾表達式表示。
5.5 求解布爾差分方程:使用布爾代數的運算規則,求解布爾差分方程,得到電路的狀態轉換關系。
-
數字電路
+關注
關注
193文章
1629瀏覽量
80822 -
時序邏輯電路
+關注
關注
2文章
94瀏覽量
16594 -
函數
+關注
關注
3文章
4346瀏覽量
62970 -
輸入信號
+關注
關注
0文章
469瀏覽量
12608
發布評論請先 登錄
相關推薦
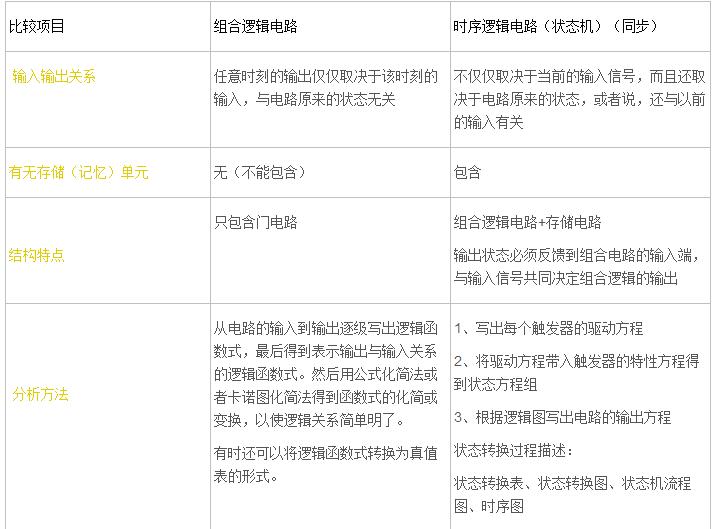
組合邏輯電路和時序邏輯電路比較_組合邏輯電路和時序邏輯電路有什么區別
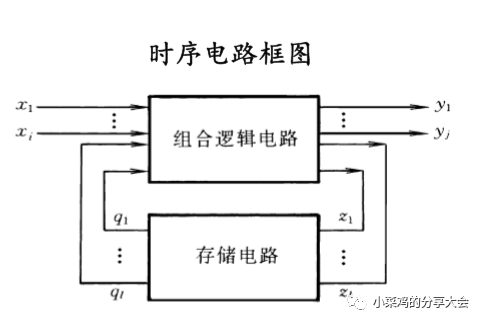
時序邏輯電路的分析方法




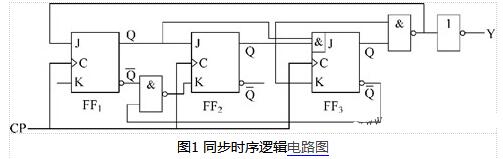
 時序邏輯電路的描述方法有哪些
時序邏輯電路的描述方法有哪些











評論