摘要
經典濾波器的濾波思路是從頻率域上將噪聲濾掉,關鍵是設計相應的濾波器傳遞函數H(s)、H(z),分別對應著模擬濾波器和數字濾波器的實現。模擬濾波器主要是通過電感(L)、電容(C)、電阻(R)和運放(OPA)等元器件搭建傳遞函數為H(s)或者近似為H(s)的硬件電路來實現,比如RC濾波電路和有源濾波器等。數字濾波器(DF)從實現的結構上或者是單位脈沖響h(n)上可以分為無限長脈沖響應(IIR)和有限長脈沖響應(FIR)濾波器。兩者在結構上的區別是:IIR有反饋回路,即當前輸出y(n)中包含以前輸出y(n-k)(k>0);FIR則沒有反饋回路,當前輸出y(n)中只包含輸入x(n)和以前的輸入x(n-k)(k>0)。正是有了反饋回路,導致了IIR單位脈沖響應h(n)的無限長。
FIR濾波器
設計流程如下圖所示(以窗函數法為例,其它方法不涉及)

IIR濾波器
設計流程如下圖所示(以巴特沃斯低通濾波器采用雙線性變換法為例)
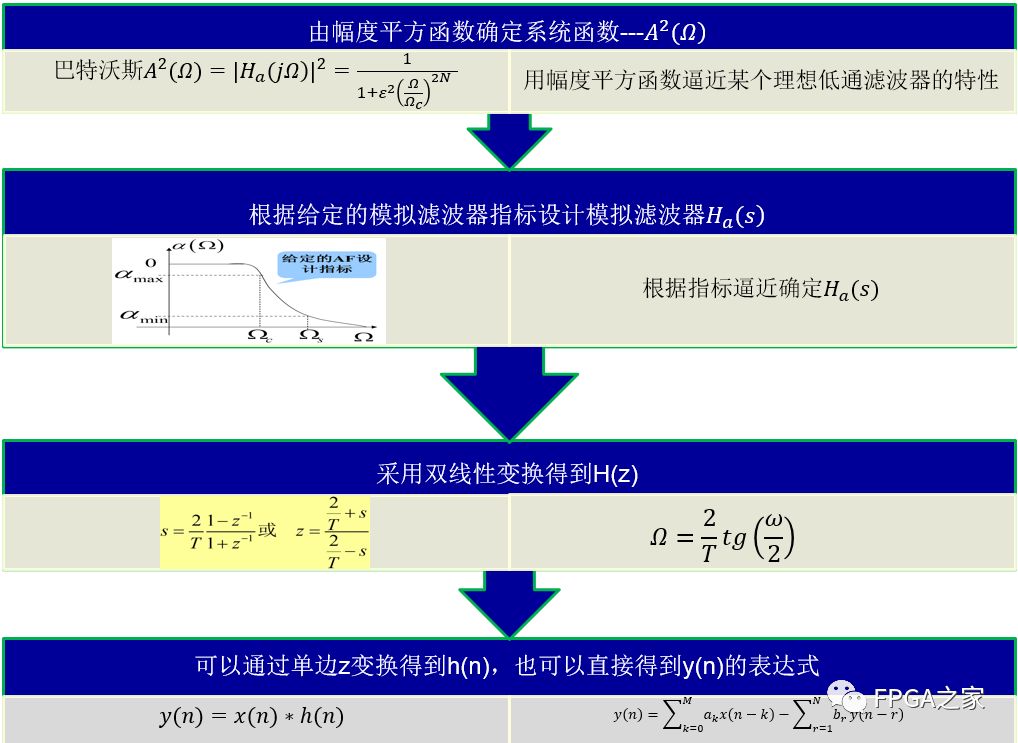
數字濾波器的實現
由上面分析,數字濾波器的兩種形式在得到的最后表達式上都可以歸一化為N階線性常系數差分方程的一般形式:
y(n)=∑Mk=0akx(n?k)?∑Nr=1bry(n?r)
這樣一個系統的實現可以分別從硬件和軟件上實現:硬件上只需要包括移位寄存器、乘法器和加法器就可以;軟件上實現就較為簡單了,直接高級語言描述。
兩種經典數字濾波器的比較
如下圖所示:
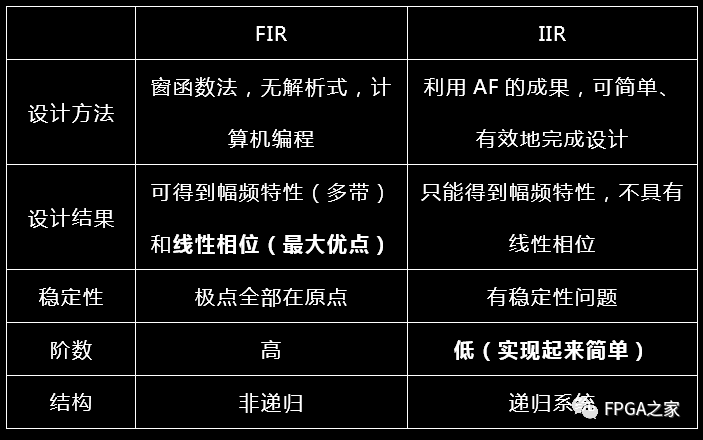
基于Matlab的實驗
用窗函數法設計FIR數字濾波器
設計一線性相位低通FIR數字濾波器,通帶截止頻率wp=0.2π,通帶最大衰減0.25dB,阻帶起始頻率ws=0.3π,阻帶最小衰減50dB。請給出N和所選窗函數,求出h(n),并繪制相應的幅頻特性(dB)曲線,根據該圖給出實際的阻帶衰減,繪制窗函數的時域頻域特性曲線。
實驗過程分析:
阻帶最小衰減為50dB,對于各種窗函數的基本參數,不能用矩形窗和漢寧窗函數,因為它們的阻帶最小衰減不能滿足設計的要求,因此可以選用漢明和布萊克曼窗進行FIR數字濾波器的設計。為了對比漢寧窗不能滿足設計要求,同樣做出漢寧窗設計的FIR數字濾波器。
根據通帶截止頻率和阻帶起始頻率得到過渡帶的帶寬,漢明窗對應的數字濾波器的過渡帶寬為8π÷N,推出用漢明窗設計時的數字濾波器的至少N=80,為了取用類型I,即偶對稱、N為奇數,取用N=81;對于用布萊克曼窗對應的數字濾波器的過渡帶寬為12π÷N,推出N=120,取N=121。漢寧窗與漢明窗的N值計算相同。
首先給出漢明窗的FIR實驗結果:
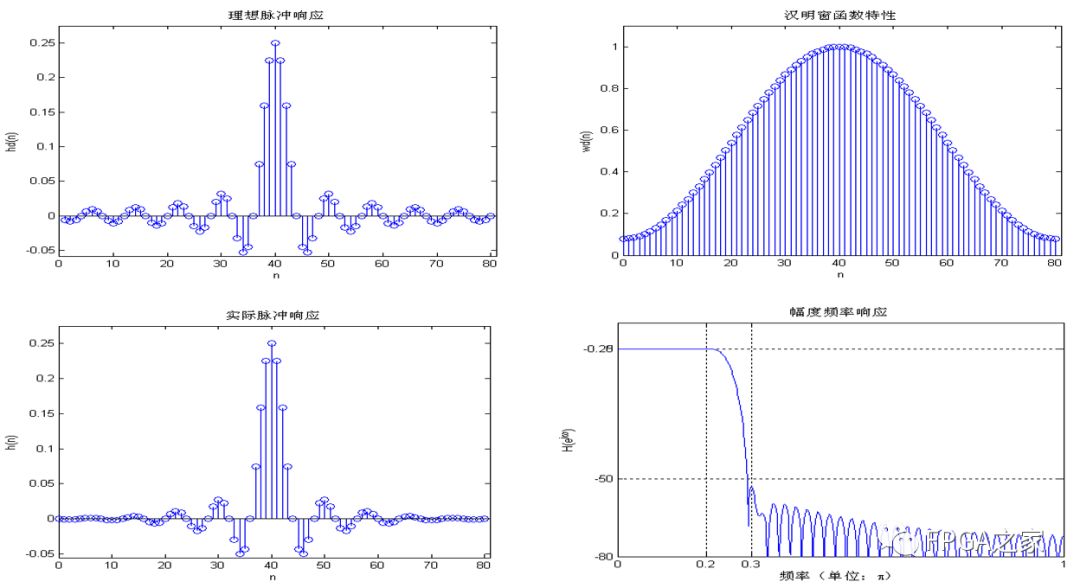
察漢明窗設計的FIR濾波器的幅頻特性曲線,在通帶內,最大衰減小于0.25db,在阻帶內,最小衰減大于50db,滿足了設計要求。
然后給出布萊克曼窗的FIR實驗結果:
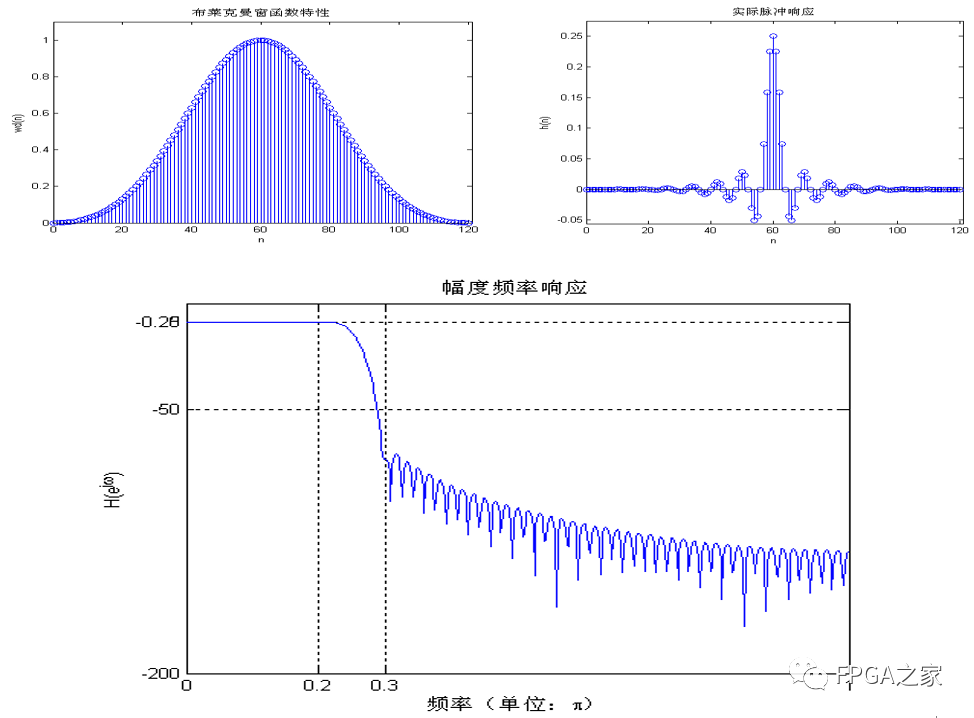
觀察布萊克曼窗設計的FIR濾波器的幅頻特性曲線,在通帶內,最大衰減小于0.25db,在阻帶內,最小衰減大于50db,滿足了設計要求。
最后給出漢寧窗的FIR實驗結果作為對比:
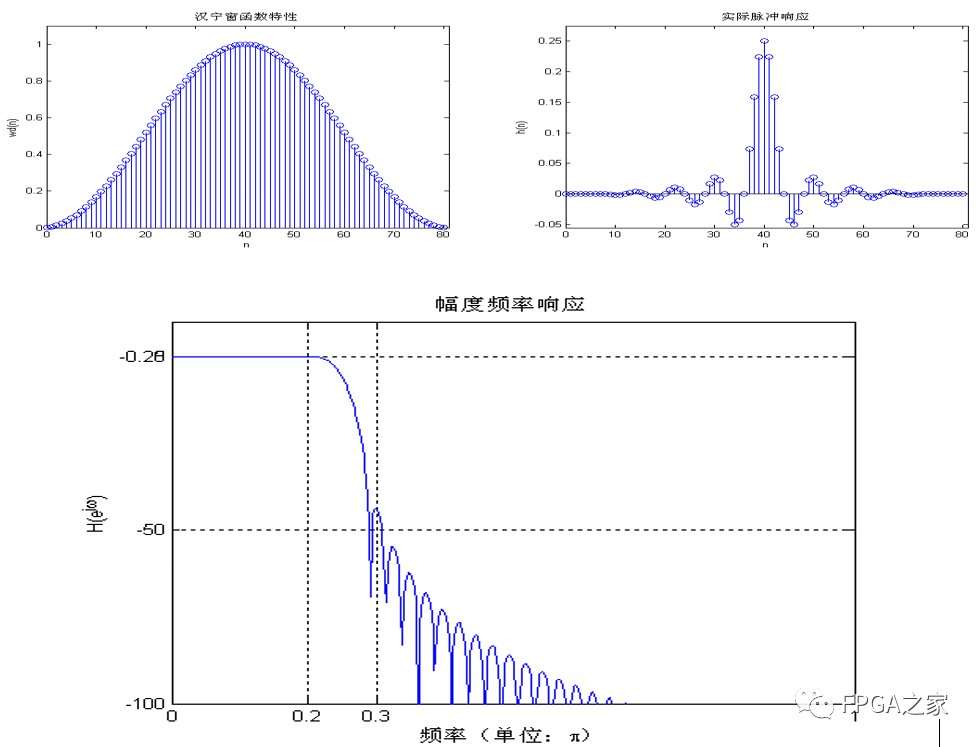
觀察漢寧窗設計的FIR濾波器的幅頻特性曲線,在通帶內,最大衰減小于0.25db,但在阻帶內最小衰減小于了50db,所以不滿足設計要求。
一般地,隨著N值增大,過渡帶愈加陡峭,衰減更快。旁瓣越多對應的通帶起伏越大。為了獲得更加平穩的通帶和更加陡峭的過渡帶,雖然不能兼得,一般處理時是通過增加主瓣寬度來換取對旁瓣的抑制。
用雙線性變換法設計IIR數字濾波器
用雙線性變換法設計一個IIR巴特沃斯低通數字濾波器。設計指標參數為:在通帶內頻率低于0.2π時,最大衰減小于1dB;在阻帶內[0.3π,π]頻率區間上,最小衰減大于15dB。用所設計的濾波器對實際心電圖信號采樣序列進行仿真濾波處理,并分別繪出濾波前后的心電圖信號波形圖。觀察總結濾波作用與效果。
實驗結果:
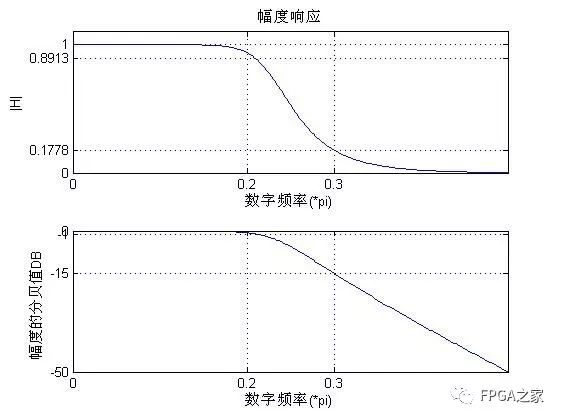
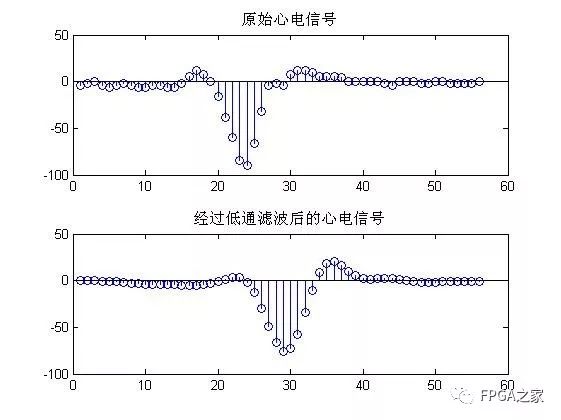
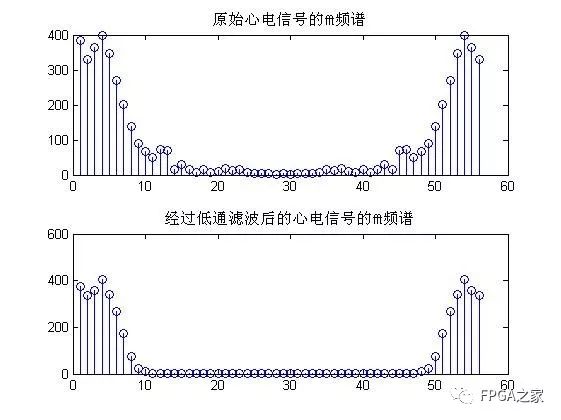
實驗結果分析:
由幅頻特性曲線可以看出設計的IIR濾波器滿足要求,同時經過心電信號的測試,能夠達到濾除高頻噪聲的目的。
本實驗中,經IIR設計的濾波器傳遞函數H(z)為:
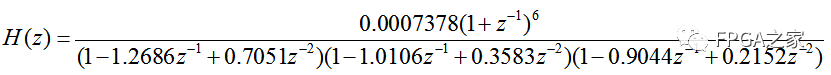
計算得到一般的線性系統表達式:
y(n)=0.0007378x(n)+0.004427x(n?1)+0.01107x(n?2)+0.01476x(n?3)+0.01107x(n?4)+0.004427x(n?5)+0.0007378x(n?6)+3.184y(n?1)?4.622y(n?2)+3.779y(n?3)?1.814y(n?4)+0.48y(n?5)?0.05445y(n?6)
一般設計濾波器就是為了得到上面的表達式,有了這樣的表達式之后就可以很方便的通過硬件或者軟件實現濾波器了。
Matlab代碼
FIR濾波器
理想低通濾波器的構建:
function hd= ideal_lp( wc,N ) %hd=點0到N-1之間的理想脈沖響應 % wc=截止頻率(弧度) %N=濾波器的長度 tao=(N-1)/2; n=[0:(N-1)]; %+eps轉換成浮點數 m=n-tao+eps; hd=sin(wc*m)./(pi*m); end
布萊克曼窗FIR濾波器:
%阻帶最小衰減為50DB,所以可以選擇漢明窗 wp=0.2*pi;ws=0.3*pi; deltaw=ws-wp;%過渡帶寬 N0=12*pi/deltaw; %N0=ceil(6.6*pi/deltaw); N=N0+mod(N0+1,2);%為實現FIR類型I偶對稱濾波器,確保N為奇數。 windows=(blackman(N))'; wc=(ws+wp)/2; hd=ideal_lp(wc,N); b=hd.*windows; [H,w]=freqz(b,1); n=0:N-1; dw=2*pi/100; dbH=20*log10((abs(H)+eps)/max(abs(H)));%化為分貝值 %Rp=-(min(db(1:wp/dw+1)))%檢驗通帶波動 %As=-round(max(db(ws/dw+1:501)))%檢驗最小阻帶衰減 %作圖 subplot(221) stem(n,hd); axis([0,N,1.1*min(hd),1.1*max(hd)]);title('理想脈沖響應'); xlabel('n'); ylabel('hd(n)'); subplot(222); stem(n,windows); axis([0,N,0,1.1]); title('布萊克曼窗函數特性'); xlabel('n'); ylabel('wd(n)'); subplot(223),stem(n,b); axis([0,N,1.1*min(b),1.1*max(b)]);title('實際脈沖響應'); xlabel('n'); ylabel('h(n)'); subplot(224); plot(w/pi,dbH); title('幅度頻率響應'); axis([0,1,-200,10]); xlabel('頻率(單位:pi)'); ylabel('H(e^{jomega})'); set(gca,'XTickMode','manual','XTick',[0,wp/pi,ws/pi,1]); set(gca,'YTickMode','manual','YTick',[-200,-50,-0.25,0]); grid
漢明窗FIR濾波器:
%阻帶最小衰減為50DB,所以可以選擇漢明窗
wp=0.2*pi;ws=0.3*pi;
deltaw=ws-wp;%過渡帶寬
N0=8*pi/deltaw;
%N0=ceil(6.6*pi/deltaw);
N=N0+mod(N0+1,2);%為實現FIR類型I偶對稱濾波器,確保N為奇數。
windows=(hamming(N))';
%windows=ones(1,N);
wc=(ws+wp)/2;
hd=ideal_lp(wc,N);
b=hd.*windows;
[H,w]=freqz(b,1);
n=0:N-1;
dw=2*pi/100;
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化為分貝值
%Rp=-(min(db(1:wp/dw+1)))%檢驗通帶波動
%As=-round(max(db(ws/dw+1:501)))%檢驗最小阻帶衰減
%作圖
figure(1)
%subplot(221)
stem(n,hd);
axis([0,N,1.1*min(hd),1.1*max(hd)]);title('理想脈沖響應');
xlabel('n');
ylabel('hd(n)');
figure(2)
%subplot(222);
stem(n,windows);
axis([0,N,0,1.1]);
title('漢明窗函數特性');
xlabel('n');
ylabel('wd(n)');
figure(3)
%subplot(223),
stem(n,b);
axis([0,N,1.1*min(b),1.1*max(b)]);title('實際脈沖響應');
xlabel('n');
ylabel('h(n)');
figure(4)
%subplot(224);
plot(w/pi,dbH);
title('幅度頻率響應');
axis([0,1,-80,10]);
xlabel('頻率(單位:pi)');
ylabel('H(e^{jomega})');
set(gca,'XTickMode','manual','XTick',[0,wp/pi,ws/pi,1]);
set(gca,'YTickMode','manual','YTick',[-80,-50,-0.25,0]);
grid
漢寧窗FIR濾波器:
%阻帶最小衰減為50DB,所以可以選擇漢明窗
wp=0.2*pi;ws=0.3*pi;
deltaw=ws-wp;%過渡帶寬
N0=8*pi/deltaw;
%N0=ceil(6.6*pi/deltaw);
N=N0+mod(N0+1,2);%為實現FIR類型I偶對稱濾波器,確保N為奇數。
windows=(hanning(N))';
wc=(ws+wp)/2;
%計算得到理想低通濾波器,已經移位(N-1)/2
hd=ideal_lp(wc,N);
%加窗施加在hn上
b=hd.*windows;
%
[H,w]=freqz(b,1);
n=0:N-1;
dw=2*pi/100;
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化為分貝值
%Rp=-(min(db(1:wp/dw+1)))%檢驗通帶波動
%As=-round(max(db(ws/dw+1:501)))%檢驗最小阻帶衰減
%作圖
subplot(221)
stem(n,hd);
axis([0,N,1.1*min(hd),1.1*max(hd)]);title('理想脈沖響應');
xlabel('n');
ylabel('hd(n)');
subplot(222);
stem(n,windows);
axis([0,N,0,1.1]);
title('漢寧窗函數特性');
xlabel('n');
ylabel('wd(n)');
subplot(223),stem(n,b);
axis([0,N,1.1*min(b),1.1*max(b)]);title('實際脈沖響應');
xlabel('n');
ylabel('h(n)');
subplot(224);
plot(w/pi,dbH);
title('幅度頻率響應');
axis([0,1,-100,10]);
xlabel('頻率(單位:pi)');
ylabel('H(e^{jomega})');
set(gca,'XTickMode','manual','XTick',[0,wp/pi,ws/pi,1]);
set(gca,'YTickMode','manual','YTick',[-100,-50,-0.25,0]);
grid
IIR數字濾波器
IIR濾波器設計:
%雙線性變換前預畸 Fs=500; wp=(100/Fs)*2*pi; ws=(200/Fs)*2*pi; Rp=2; Rs=15; wp2=2*Fs*tan(wp/2); ws2=2*Fs*tan(ws/2); %選擇濾波器的最小階數 [N,wn]=buttord(wp2,ws2,Rp,Rs,'s');%注意此處輸入的是畸變后的指標,輸出N為符合要求的模擬濾波器的最小階數,wn為3dB帶寬 %創建butterworth模擬濾波器 [Z,P,K]=buttap(N); %把濾波器零極點模型轉化為傳遞函數模型 [Bap,Aap]=zp2tf(Z,P,K); %把模擬濾波器原型轉換為截止頻率為wn的模擬低通濾波器 [b,a]=lp2lp(Bap,Aap,wn); %用雙線性法實現模擬濾波器到數字濾波器的轉換 [bz,az]=bilinear(b,a,Fs); %繪制頻率響應曲線 [H,W]=freqz(bz,az); subplot(2,1,1); plot(W/pi,abs(H)); grid; xlabel('頻率w/pi'); ylabel('幅度絕對值'); subplot(2,1,2); plot(W/pi,20*log10((abs(H)+eps)/max(abs(H)))); grid; xlabel('頻率w/pi'); ylabel('幅度dB');
心電信號濾波:
%數字濾波器指標: wc=0.2*pi;ws=0.3*pi;Rp=1;As=15; ripple=10^(-Rp/20);Attn=10^(-As/20); %轉換成為模擬指標: Fs=1;T=1/Fs; Omgp=(2/T)*tan(wc/2); Omgs=(2/T)*tan(ws/2); %模擬原型濾波器計算: [n,Omgc]=buttord(Omgp,Omgs,Rp,As,'s');%計算階數和截止頻率 [z0,p0,k0]=buttap(n); ba=k0*real(poly(z0)); aa=real(poly(p0)); [ba1,aa1]=lp2lp(ba,aa,Omgc); %雙線性變換法計算數字濾波器系數 [bd,ad]=bilinear(ba1,aa1,Fs);%雙線性變換法求數字濾波器系數b,a tf(bd,ad,1) [sos,g]=tf2sos(bd,ad)%由直接型轉變成級聯型 %求數字系統的頻率特性: [H,w]=freqz(bd,ad); dbH=20*log10((abs(H)+eps)/max(abs(H)));%化為分貝值 subplot(2,1,1); plot(w/pi,abs(H)); % 加上對應取值軸來驗證是否滿足設計要求 set(gca,'XTickMode','Manual','XTick',[0,0.2,0.3,pi]) set(gca,'YTickMode','Manual','YTick',[0,Attn,ripple,1]) ylabel('|H|'); xlabel('數字頻率(*pi)') title('幅度響應'); axis([0,1/2,0,1.1]); grid on subplot(212); plot(w/pi,dbH); xlabel('數字頻率(*pi)'); ylabel('幅度的分貝值DB'); % 加上對應取值軸來驗證是否滿足設計要求 set(gca,'XTickMode','Manual','XTick',[0,0.2,0.3,pi]) set(gca,'YTickMode','Manual','YTick',[-50,-As,-Rp,0]) axis([0,1/2,-50,0.1]); grid on %心電信號: xn=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,... 0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4,8,12,12,10,6,... 6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0] figure; subplot(211); stem(xn); title('原始心電信號') yn=filter(bd,ad,xn); subplot(212); stem(yn); title('經過低通濾波后的心電信號') figure; subplot(211); stem(abs(fft(xn))); title('原始心電信號的fft頻譜') yn=filter(bd,ad,xn); subplot(212); stem(abs(fft(yn)));
title('經過低通濾波后的心電信號的fft頻譜');
-
濾波器
+關注
關注
161文章
7860瀏覽量
178926 -
fir濾波器
+關注
關注
1文章
95瀏覽量
19093 -
IIR濾波器
+關注
關注
0文章
33瀏覽量
11565
原文標題:經典濾波器設計
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
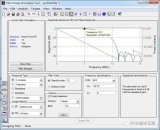
Vivado經典案例:使用Simulink設計FIR濾波器
頻率濾波器怎么分類?
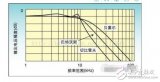
濾波器有幾種?四種濾波器之間對比詳解
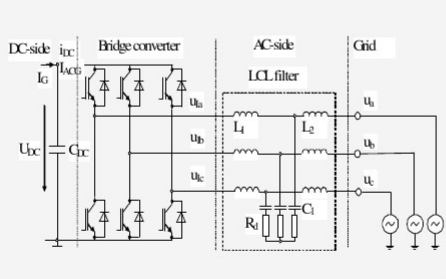
光伏并網逆變器LCL濾波器的設計資料說明
階躍阻抗諧振器的結構原理和實現微帶帶通濾波器的設計說明
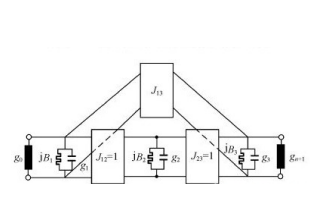
LC濾波器的設計和應用資料說明





 經典濾波器的設計說明
經典濾波器的設計說明











評論