感知機(jī)是個(gè)相當(dāng)簡(jiǎn)單的模型，但它既可以發(fā)展成支持向量機(jī)（通過(guò)簡(jiǎn)單地修改一下?lián)p失函數(shù)）、又可以發(fā)展成神經(jīng)網(wǎng)絡(luò)（通過(guò)簡(jiǎn)單地堆疊），所以它也擁有一定的地位

為方便，我們統(tǒng)一討論二分類(lèi)問(wèn)題，并將兩個(gè)類(lèi)別的樣本分別稱為正、負(fù)樣本

感知機(jī)能做什么？

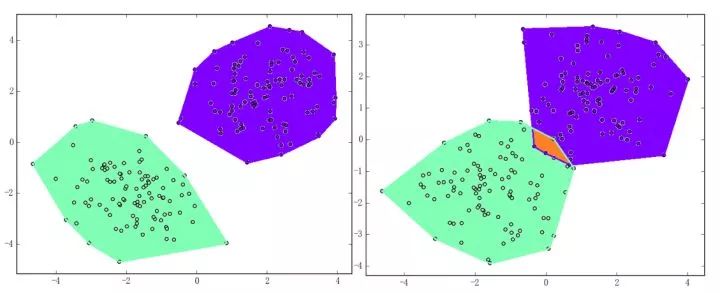
感知機(jī)能（且一定能）將線性可分的數(shù)據(jù)集分開(kāi)。什么叫線性可分？在二維平面上、線性可分意味著能用一條線將正負(fù)樣本分開(kāi)，在三維空間中、線性可分意味著能用一個(gè)平面將正負(fù)樣本分開(kāi)。可以用兩張圖來(lái)直觀感受一下線性可分（上圖）和線性不可分（下圖）的概念：

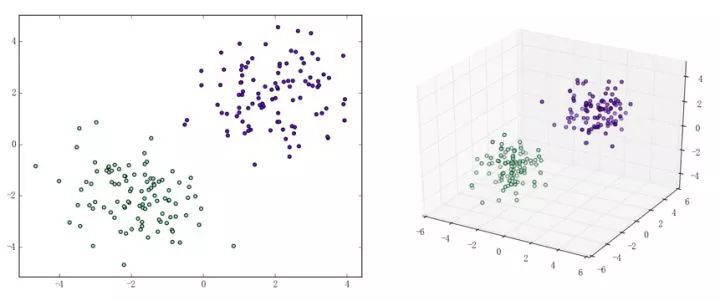
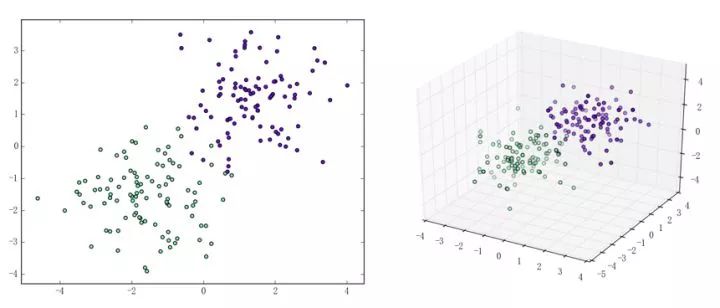
那么一個(gè)感知機(jī)將會(huì)如何分開(kāi)線性可分的數(shù)據(jù)集呢？下面這兩張動(dòng)圖或許能夠給觀眾老爺們一些直觀感受：

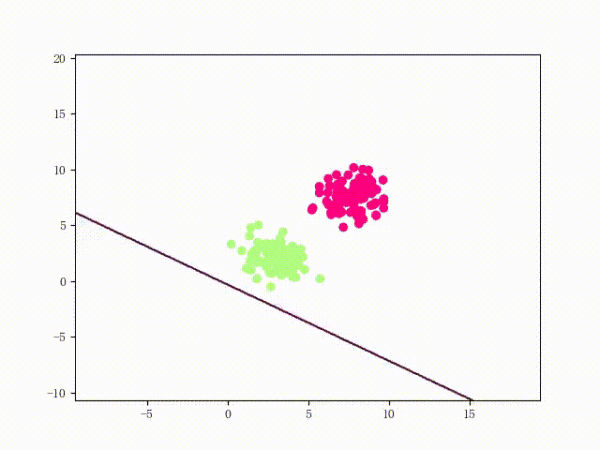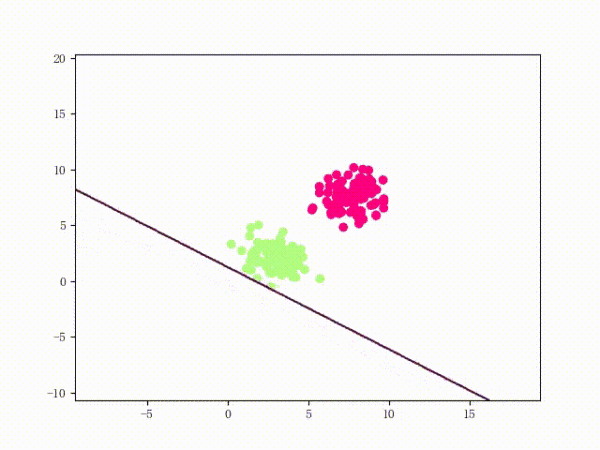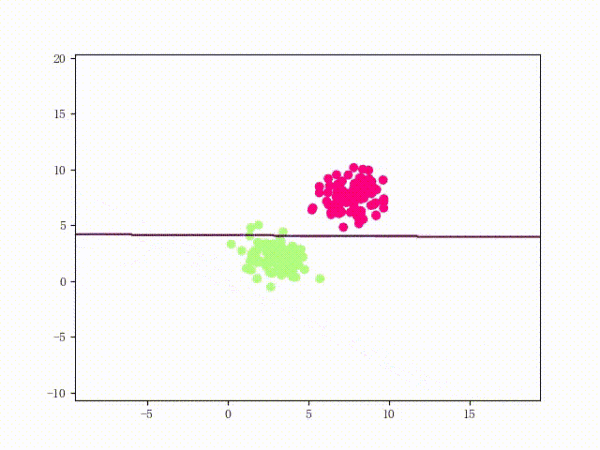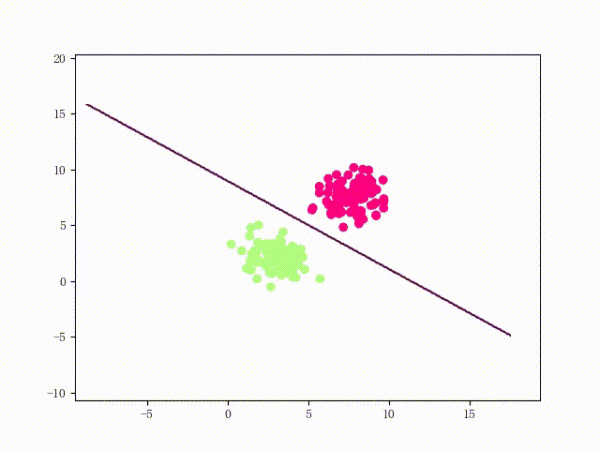
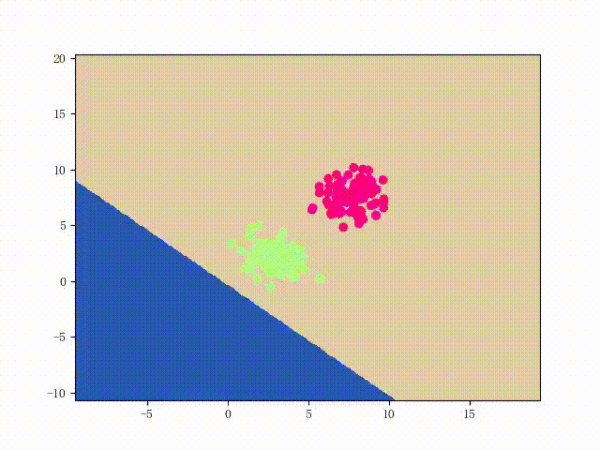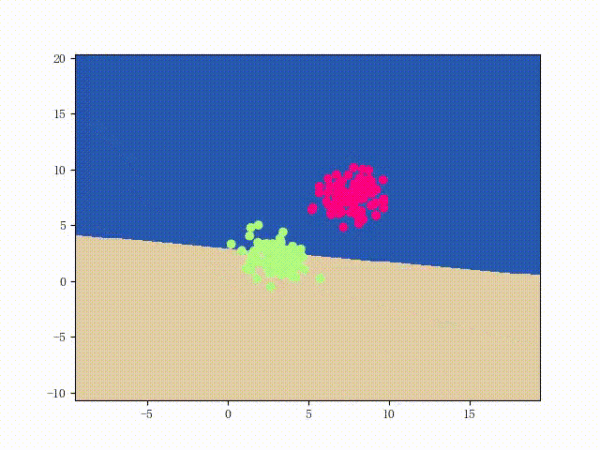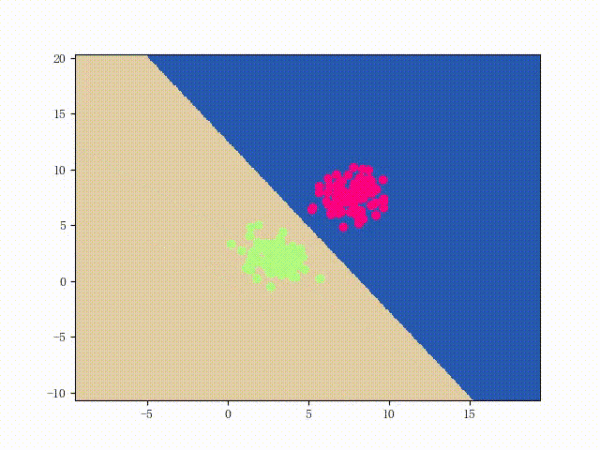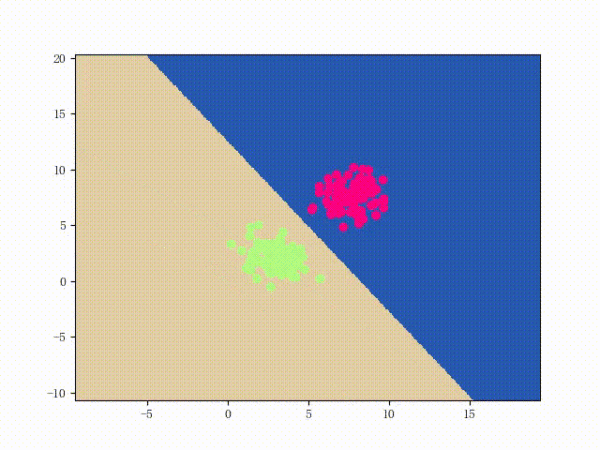
看上去挺捉急的，不過(guò)我們可以放心的是：只要數(shù)據(jù)集線性可分，那么感知機(jī)就一定能“蕩”到一個(gè)能分開(kāi)數(shù)據(jù)集的地方（文末會(huì)附上證明）

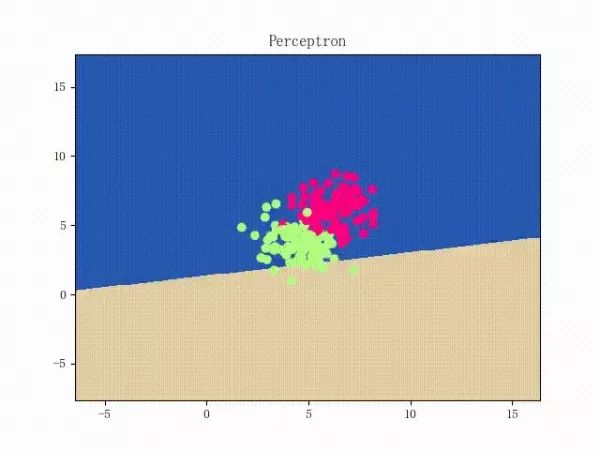
那么反過(guò)來(lái)，如果數(shù)據(jù)集線性不可分，那么感知機(jī)將如何表現(xiàn)？相信聰明的觀眾老爺們已經(jīng)猜到了：它將會(huì)一直“蕩來(lái)蕩去”（最后停了是因?yàn)榈搅说舷蓿ㄈ缓竺菜苿?dòng)圖太大導(dǎo)致有殘影……不過(guò)效果也不差所以就將就著看一下吧 ( σ'ω')σ）：

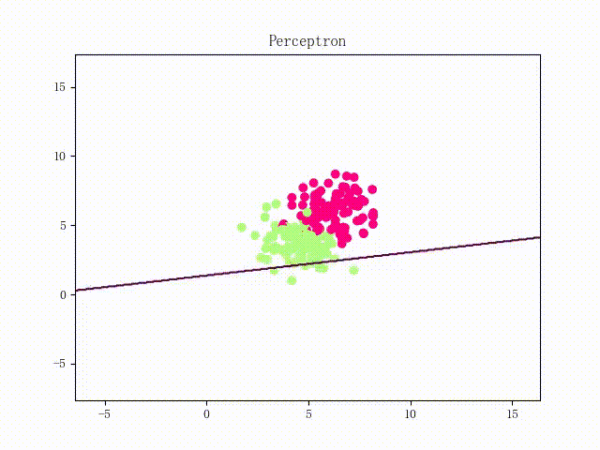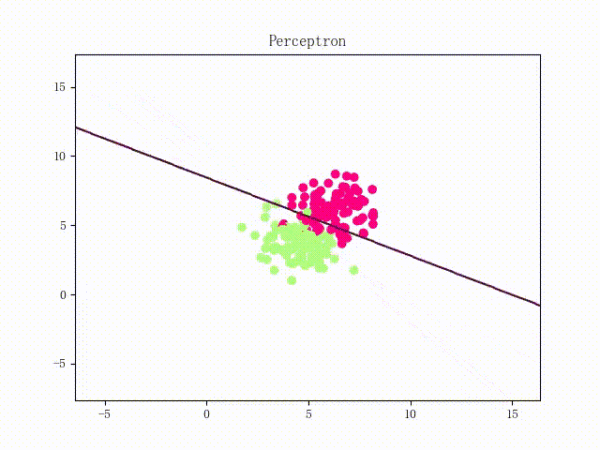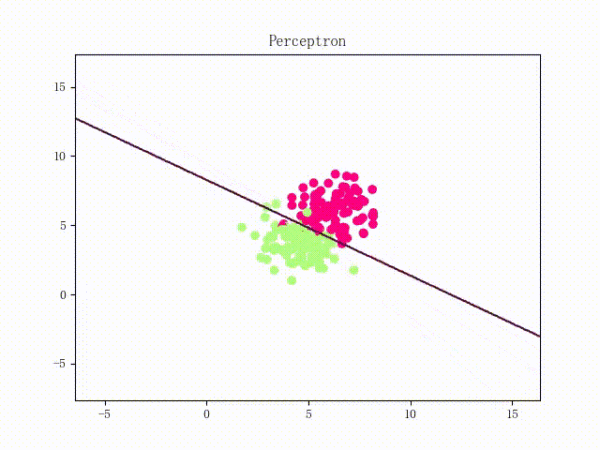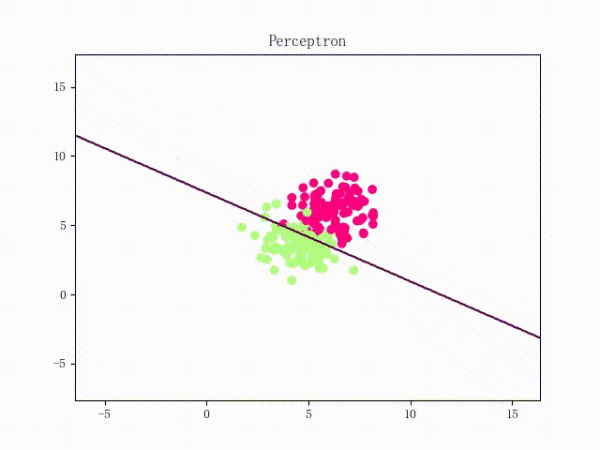
class Perceptron: def __init__(self): self._w = self._b = None def fit(self, x, y, lr=0.01, epoch=1000): # 將輸入的 x、y 轉(zhuǎn)為 numpy 數(shù)組 x, y = np.asarray(x, np.float32), np.asarray(y, np.float32) self._w = np.zeros(x.shape[1]) self._b = 0.

上面這個(gè) fit 函數(shù)中有個(gè) lr 和 epoch，它們分別代表了梯度下降法中的學(xué)習(xí)速率和迭代上限（p.s. 由后文的推導(dǎo)我們可以證明，對(duì)感知機(jī)模型來(lái)說(shuō)、其實(shí)學(xué)習(xí)速率不會(huì)影響收斂性【但可能會(huì)影響收斂速度】）

梯度下降法我們都比較熟悉了。簡(jiǎn)單來(lái)說(shuō)，梯度下降法包含如下兩步：

求損失函數(shù)的梯度（求導(dǎo)）

梯度是函數(shù)值增長(zhǎng)最快的方向我們想要最小化損失函數(shù)我們想讓函數(shù)值減少得最快將參數(shù)沿著梯度的反方向走一步

（這也是為何梯度下降法有時(shí)被稱為最速下降法的原因。梯度下降法被普遍應(yīng)用于神經(jīng)網(wǎng)絡(luò)、卷積神經(jīng)網(wǎng)絡(luò)等各種網(wǎng)絡(luò)中，如有興趣、可以參見(jiàn)這篇文章(https://zhuanlan.zhihu.com/p/24540037)）

那么對(duì)于感知機(jī)模型來(lái)說(shuō)，損失函數(shù)是什么呢？注意到我們感知機(jī)對(duì)應(yīng)的超平面為

for _ in range(epoch): # 計(jì)算 w·x+b y_pred = x.dot(self._w) + self._b # 選出使得損失函數(shù)最大的樣本 idx = np.argmax(np.maximum(0, -y_pred * y)) # 若該樣本被正確分類(lèi)，則結(jié)束訓(xùn)練 if y[idx] * y_pred[idx] > 0: break # 否則，讓參數(shù)沿著負(fù)梯度方向走一步 delta = lr * y[idx] self._w += delta * x[idx] self._b += delta

那么一個(gè)感知機(jī)將會(huì)如何分開(kāi)線性可分的數(shù)據(jù)集呢？下面這兩張動(dòng)圖或許能夠給觀眾老爺們一些直觀感受：

至此，感知機(jī)模型就大致介紹完了，剩下的則是一些純數(shù)學(xué)的東西，大體上不看也是沒(méi)問(wèn)題的（趴

相關(guān)數(shù)學(xué)理論

亦即訓(xùn)練步數(shù)是有上界的，這意味著收斂性。而且中不含學(xué)習(xí)速率，這說(shuō)明對(duì)感知機(jī)模型來(lái)說(shuō)、學(xué)習(xí)速率不會(huì)影響收斂性

最后簡(jiǎn)單介紹一個(gè)非常重要的概念：拉格朗日對(duì)偶性（Lagrange Duality）。我們?cè)谇叭」?jié)介紹的感知機(jī)算法，其實(shí)可以稱為“感知機(jī)的原始算法”；而利用拉格朗日對(duì)偶性，我們可以得到感知機(jī)算法的對(duì)偶形式。鑒于拉格朗日對(duì)偶性的原始形式太過(guò)純數(shù)學(xué)，所以我打算結(jié)合具體的算法來(lái)介紹、而不打算敘述其原始形式，感興趣的觀眾老爺可以參見(jiàn)這里（https://en.wikipedia.org/wiki/Duality_(optimization)）

在有約束的最優(yōu)化問(wèn)題中，為了便于求解、我們常常會(huì)利用它來(lái)將比較原始問(wèn)題轉(zhuǎn)化為更好解決的對(duì)偶問(wèn)題。對(duì)于特定的問(wèn)題，原始算法的對(duì)偶形式也常常會(huì)有一些共性存在。比如對(duì)于感知機(jī)和后文會(huì)介紹的支持向量機(jī)來(lái)說(shuō)，它們的對(duì)偶算法都會(huì)將模型的參數(shù)表示為樣本點(diǎn)的某種線性組合、并把問(wèn)題轉(zhuǎn)化為求解線性組合中的各個(gè)系數(shù)

雖說(shuō)感知機(jī)算法的原始形式已經(jīng)非常簡(jiǎn)單，但是通過(guò)將它轉(zhuǎn)化為對(duì)偶形式、我們可以比較清晰地感受到轉(zhuǎn)化的過(guò)程，這有助于理解和記憶后文介紹的、較為復(fù)雜的支持向量機(jī)的對(duì)偶形式

考慮到原始算法的核心步驟為：

此即感知機(jī)模型的對(duì)偶形式。需要指出的是，在對(duì)偶形式中、樣本點(diǎn)里面的x僅以內(nèi)積的形式（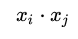

注意到對(duì)偶形式的訓(xùn)練過(guò)程常常會(huì)重復(fù)用到大量的、樣本點(diǎn)之間的內(nèi)積，我們通常會(huì)提前將樣本點(diǎn)兩兩之間的內(nèi)積計(jì)算出來(lái)并存儲(chǔ)在一個(gè)矩陣中；這個(gè)矩陣就是著名的 Gram 矩陣、其數(shù)學(xué)定義即為：

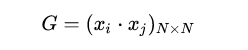
從而在訓(xùn)練過(guò)程中如果要用到相應(yīng)的內(nèi)積、只需從 Gram 矩陣中提取即可，這樣在大多數(shù)情況下都能大大提高效率