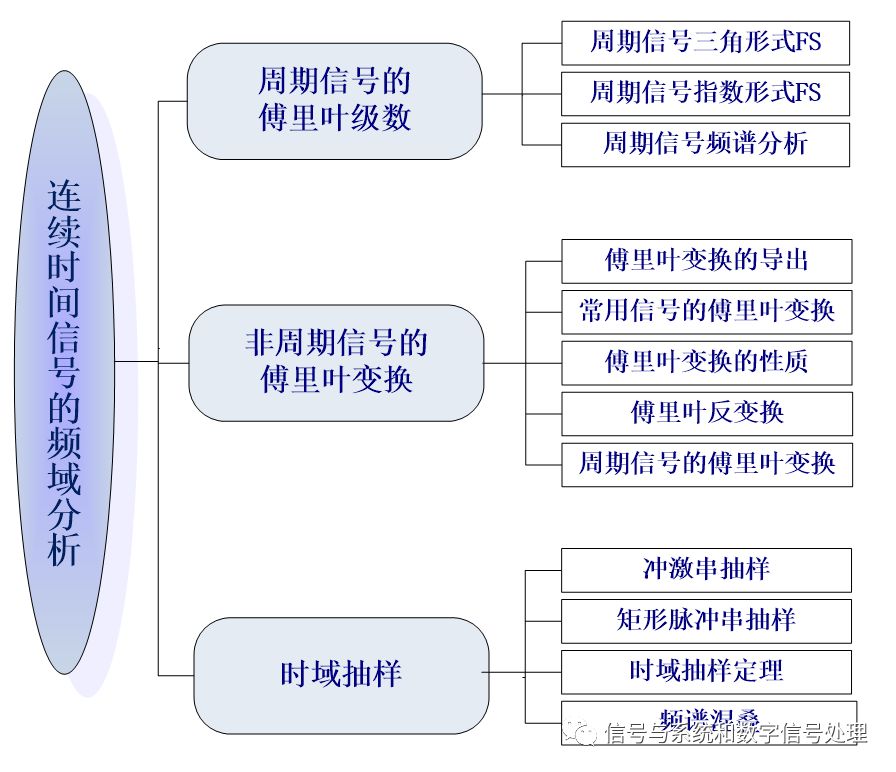
連續時間信號的頻域分析,是本課程最為重要的內容之一,也是考試的重點。包括三方面內容:周期信號的傅里葉級數、非周期信號的傅里葉變換、時域抽樣。具體內容如下圖所示。
本文包括前面兩部分:周期信號的傅里葉級數、非周期信號的傅里葉變換。
說在前頭:
借助傅里葉級數這塊敲門磚,我們就可以邁進頻域分析的世界。但是很不幸,傅里葉級數稍顯繁瑣的表示形式和推導過程,使很多人望而生畏,打擊了學好本課程的自信心,越學越不想學,甚至于放棄。所以,我要求大家在學習或復習傅里葉級數這部分內容的時候,要練就一顆火眼金睛,要透過繁瑣的數學推導和計算,看到它背后隱藏的物理意義。特別是到傅里葉變換這部分,會出現很多神奇而美妙的結論,就好比閃閃發光的珠寶,吸引大家學好信號與系統。
一、周期信號的傅里葉級數(CTFS)
“周期信號的傅里葉級數”是打開“頻域分析”大門的敲門磚,是連接時域和頻域的橋梁。
主要內容包括:
1、三角形式的FS和指數形式的FS
下圖給出了三角形式和指數形式的FS展開式及系數求解公式。


三角形式的FS與指數形式的FS的根本不同之處在于下面這個式子:
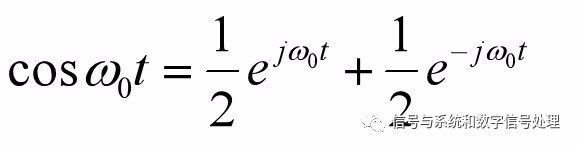
指數形式傅氏級數中有負頻率項,只是表達形式的問題,并不表示真正存在以負頻率進行振蕩的分量,負頻率項與相應的正的頻率項合起來才代表一個振蕩分量。
需要掌握:
第一,兩種形式的正交信號集的特點;
第二,兩種形式的FS的展開式的表達式及系數求解(重點)。
根據周期信號時域表達式的不同,求解方法分為兩種:
第一種,當信號直接寫成幾個正余弦函數之和的形式時,直接與FS展開式的標準形式對比,得出FS系數,例如:


第二種,一般的周期信號,則需要利用系數求解公式進行積分運算。例如周期矩形脈沖信號的FS。教材上一般都有這道例題,這里不再重復。
2、周期信號的頻譜分析
這里是本課程首次給出“頻譜”的概念。用頻譜來描述信號,大家一定要接受并掌握這種描述信號的新形式,理清時頻對應關系,為后續課程的學習打下基礎。
第一,掌握頻譜的概念。衍生出來的“幅度譜”、“相位譜”、“單邊譜”、“雙邊譜”等名詞。
再從做題的角度總結一下,如下圖。

第二,周期信號頻譜的特點:離散性、諧波性、收斂性
第三,周期信號時域參數與頻譜特性的關系
以周期矩形脈沖信號為例來分析。如下圖。
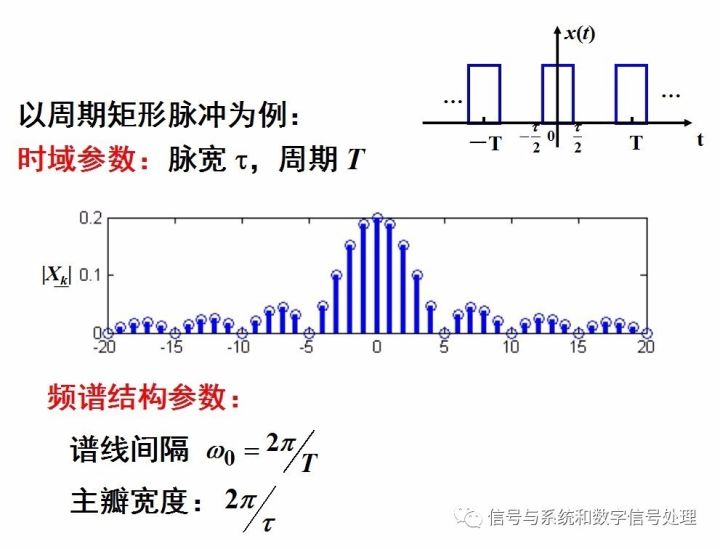
得到以下結論:

第四,時域波形對稱特點與傅里葉系數的關系
如果時域波形有某種對稱的特點,它的傅里葉級數會表現出一些特殊性,如下圖所示。
這種特殊性,在求解一些周期信號的傅里葉級數系數時,如果運用得當,可以簡化計算。

二、非周期信號的傅里葉變換(CTFT)
傅里葉變換是重點中的重點。包括以下幾個方面的內容:
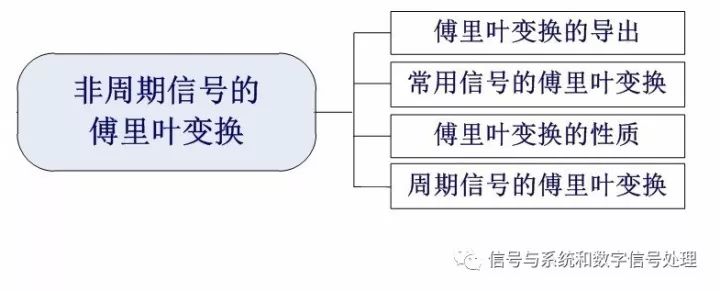
1、傅里葉變換的導出
如下圖所示。
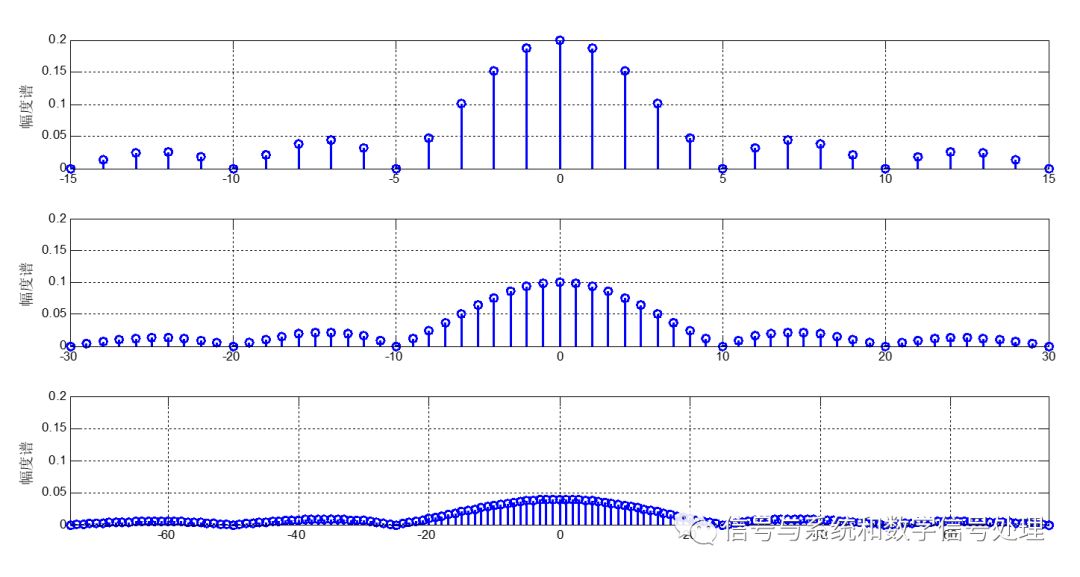
周期T→無窮大,譜線間隔→無窮小,離散譜→連續譜,但同時,譜線幅度→無窮小,此時,用FS表示頻譜就不合適了。我們注意到,雖然譜線幅度趨于無窮小,但相對大小依然有區別。
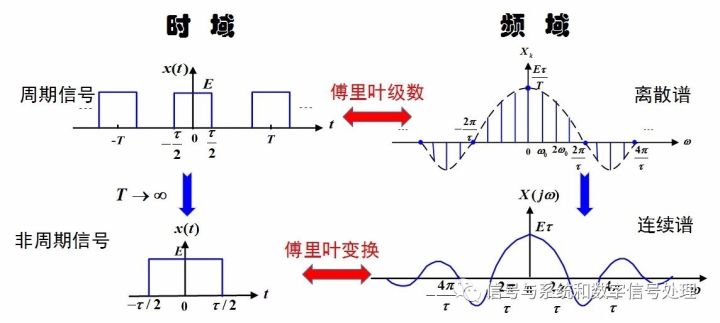
借助物理上的“密度”的概念,質量/體積=密度。導出非周期信號的傅里葉變換X(jw),它的意義是單位頻帶上的頻譜值,稱為“頻譜密度函數”。
2、常用信號的傅里葉變換
沖激信號、階躍信號、符號函數、直流信號、正弦信號、余弦信號、單邊指數衰減信號、雙邊指數衰減信號、門函數(矩形脈沖信號)、鐘形脈沖信號(高斯脈沖)、升余弦脈沖信號、sinc函數等等。以及它們的各階導數和微分。
這些常用信號,有普通信號,也有奇異信號;有滿足絕對可積條件的,也有不滿足絕對可積條件的。它們的傅里葉變換的求解,分為三種情況:
第一種,直接利用定義式求解;第二種,利用已有的變換對和性質求解;第三種,特殊方法(比如階躍信號u(t)、符號函數等)。
有些要記住、有些(比如雙邊指數信號、鐘形脈沖、升余弦脈沖等)要能推導出來。

3、傅里葉變換的性質
利用傅里葉變換這個工具,我們可以從信號的時域描述(以時間t為自變量的函數x(t))得到它的頻域描述(X(jw)),反之亦然。傅里葉變換的性質就是研究這兩個域——時域和頻域之間的對應關系,什么對應關系呢?我們可以用兩句話來總結,第一句話,一個域中的某些特性在另外一個域中對應什么特性?第二句話,一個域中的某種運算在另外一個域中發生什么變化?具體來說,哪些特性、哪些運算呢?比如,奇偶對稱特性、展縮運算、平移、積分/微分等等。
任何一本教材上,都有傅里葉變換性質的列表,這里不面面俱到。重點講以下幾個:
展縮特性
矩形脈沖信號的傅里葉變換對能特別直觀地展現展縮性質。
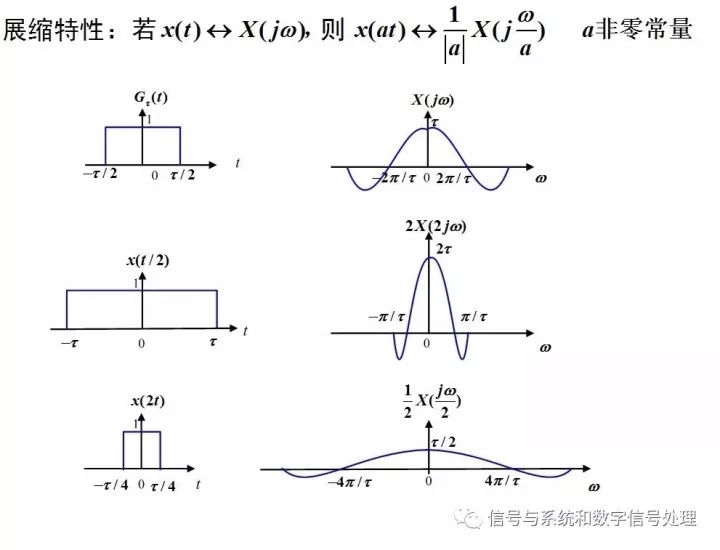
矩形脈沖的脈寬增大,時域上,非零值的時間范圍增加;頻域上,頻譜更集中在頻率原點附近。即“時域擴展,頻譜壓縮”,反之亦然。
展縮特性,從理論上證明了時域與頻域的相反關系,也證明了信號的時寬帶寬積等于常數的結論。通信中,若要壓縮信號的持續時間,則信號的帶寬就要展寬。要壓縮信號的有效頻帶,就不得不增加信號的持續時間。
一般而言,時域有限,頻譜無限,反之亦然。不存在時域和頻域都有限的信號。
時移頻移特性
時域平移,對應頻域,幅頻特性不變,相位譜產生附加的線性變化(+wt0)。所以波形的形狀不變,因為各個頻率分量的相對大小關系不變(對應幅度譜不變)、在時間軸上的相對位置關系也不變(對應相位增加一個wt0,和w成線性關系)。
頻移呢,頻譜的搬移是通信系統中應用廣泛的技術,例如調制、解調、變頻等,都是在頻移的基礎上完成的,頻移特性是其理論基礎。
利用頻移特性,我們可以推導出虛指數信號、正弦余弦信號的傅里葉變換。這三個信號都是不滿足絕對可積條件的,其傅里葉變換中都存在沖激函數。
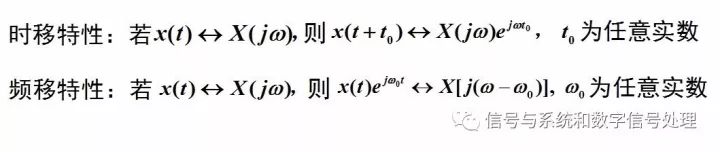
微分特性
時域微分特性和頻域微分特性,可以用來求解利用公式不能或者不易求解的變換對,比如沖激偶函數、tu(t)等等。
微分特性,在系統的頻域分析中很重要。因為描述連續時間系統的是微分方程,我們可以想到,傅里葉變換的方法,必將在微分方程求解(即系統響應求解)、系統分析中大有用武之地。
積分特性
積分特性也是主要用來求解一些比較復雜的信號的傅里葉變換。但是應用的時候要注意,不能把積分特性當做微分特性的倒過來,而要注意其中的直流分量,否則就會出錯。
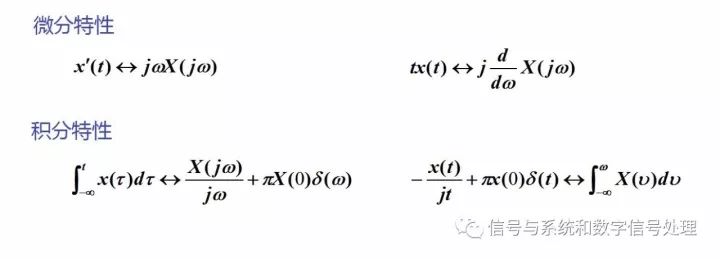
卷積特性
包括時域卷積特性和頻域卷積特性,一個域相乘,另外一個域卷積,這是一個非常基本、非常重要的關系。
提供了一種計算傅里葉變換的方法,同時,也是系統的頻域分析的基礎。
互易對稱特性
最后來說一說這個神奇而美麗的性質。
如果某個信號,在時域上有某種紅色的特性,它在頻域上有藍色的特性,而另外一個信號,在時域上有這種藍色的特性,那么它在頻域上,就會以某種類似于剛才那種紅色的特性表現出來。
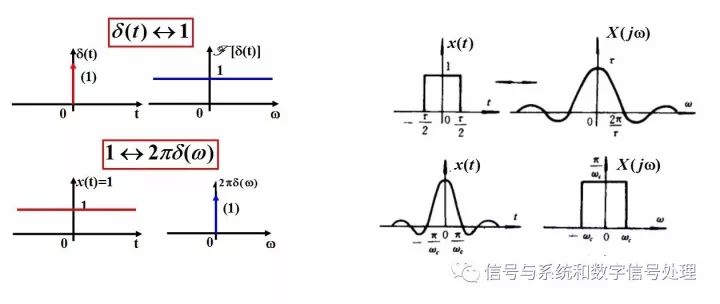
很多變換對體現了這一點。比如,時域上的沖激信號,頻譜是1;而時域上的直流1,對應頻譜為2π乘上沖激函數。再比如,時域上的矩形脈沖,頻譜為sinc函數;而時域的sinc信號,頻譜為矩形函數。
很多傅里葉變換的性質也體現了這一點,比如時移特性與頻移特性、時域微分與頻域微分,等等。

最后,提一下傅里葉反變換的求解方法,有以下三種:
利用傅里葉反變換的定義式求解
利用FT的性質求解
特別注意互易對稱性的應用。
部分分式展開法
部分分式展開法,不僅僅是傅里葉反變換的求解方法之一,也是后面的拉氏變換、z變換的反變換求解方法。
4、周期信號的傅里葉變換
周期信號,不滿足絕對可積,如果帶入到傅里葉變換的公式里,積分是不收斂的,那是不是就意味著,周期信號的傅里葉變換不存在呢?不是的。我們前面在講解傅里葉變換的性質時,已經求解出了正余弦信號的傅里葉變換對,發現它們的傅里葉變換中有沖激函數,所以,通過引入沖激函數,不滿足絕對可積條件的周期信號,也可以用傅里葉變換來表示。這樣,傅里葉變換就把傅里葉級數統一起來了。
傅里葉級數和傅里葉變換之間到底是什么關系呢?用下圖很容易理解二者的關系。
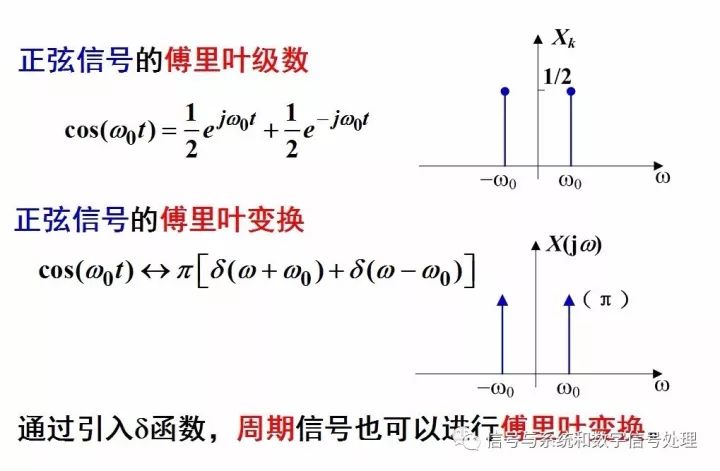
周期信號的傅里葉變換是一系列強度為2πXk,發生在諧波頻率kw0上的沖激串的線性組合,仍是離散譜。
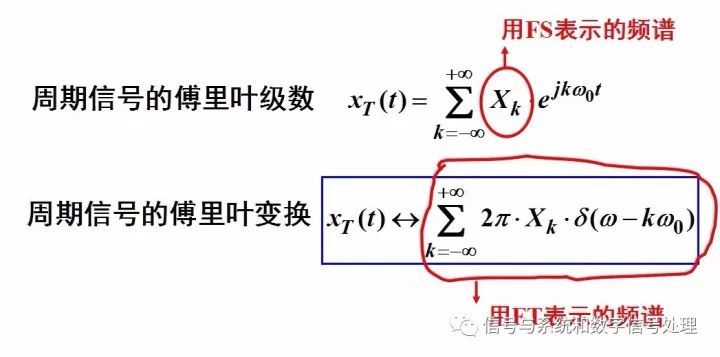
可以推導出一個非常重要、非常有趣、非常美麗的一個變換對,如下圖
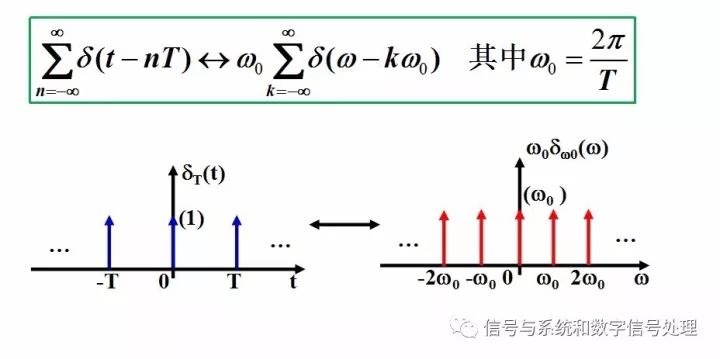
上圖所示的這個變換對,會在“時域抽樣”部分中發揮重要的作用。
-
頻域分析
+關注
關注
0文章
20瀏覽量
12749 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42708 -
連續時間信號
+關注
關注
0文章
3瀏覽量
2554 -
傅里葉級數
+關注
關注
1文章
11瀏覽量
2471
原文標題:“連續時間信號的頻域分析”知識脈絡(之一)
文章出處:【微信號:SignalAndSystem_DSP,微信公眾號:信號與系統和數字信號處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 連續時間信號頻域周期信號傅里葉級數和非周期信號傅里葉變換的分析
連續時間信號頻域周期信號傅里葉級數和非周期信號傅里葉變換的分析
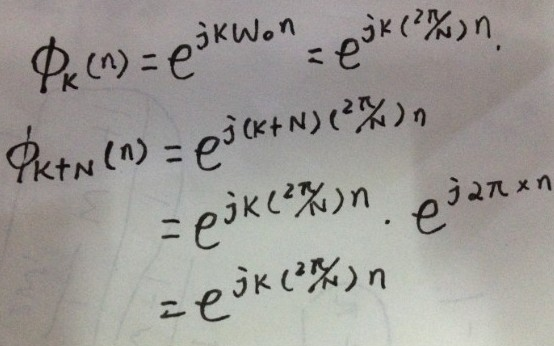










評論