本文主要是基于 Vertibi算法的卷積碼解碼設計實現的相關介紹，并就卷積編碼展開了詳盡的闡述。

卷積編碼

在信道編碼研究的初期，人們探索、研究出各種各樣的編碼構造方法，其中包括卷積碼。早在1955年，P.Elias首先提出了卷積碼。但是它又經歷了十幾年的研究以后，才開始具備應用價值。在這十幾年期間，J.M.Wozencraft提出了適合大編碼約束度的卷積碼的序列譯碼，J.L.Massey提出了實現簡單的門限譯碼，A.J.Viterbi提出了適合小編碼約束度的卷積碼Viterbi算法。20年后，即1974年，L.R.Bahl等人又提出一種支持軟輸入軟輸出（SISO，Soft-Input Soft-Output）的最大后驗概率（MAP，Maximum A Posteriori）譯碼——BCJR算法。其中，Viterbi算法有力地推動了卷積碼的廣泛應用，BCJR算法為后續Turbo碼的發現奠定了基礎。

淺談卷積編碼

實際上編碼過程就可以應用一個經典的“狀態機模型”，而狀態機模型的不同表達方式也使得整個編碼過程在時間和空間兩個維度展現出來。例如，狀態圖，即是一個很好的表示狀態變化的圖形。但是由于循環反復的利用狀態信息，但在時間上，并未很好的體現卷積碼的編碼過程。相比，樹形圖，在時間上進行延展，很直觀的表現出狀態變化的過程，但是狀態信息未重復利用，使得存儲空間大小得到限制（指數增加）。最后，網格圖很好的展現了時間和空間兩個維度信息，很適合分析卷積碼的編碼過程。而用Matlab實現卷積碼編碼的時候，我按照傳統卷積碼編碼方法（只考慮實現，未考慮算法的優化），中規中矩的編碼思路，但在速度上，并未得到很好的保證。而老師給的編程思想則是：給出每個以為寄存器中隨時間變化存儲的二進制信息。例如，4個移位寄存器，則每個移位寄存器存儲的信息分別為：[abcdefg000；0abcdefg00；00abcdefg0；000abcdefg]，所以矩陣的縱列信息即為所有寄存器中瞬時狀態信息，而生成多項式中數值為‘1’的移位寄存器存儲比特信息將參與mod2運算。這樣利用矩陣的乘法直接完成查找移位寄存器中對應生成多項式數值為‘1’位置的信息。相比我的編碼思路（循環查找寄存器里對應生成多項式數值為‘1’的信息），運算速度大大提升。同時，在對狀態機模型的認識也進一步深入，即，編碼過程為移位寄存器中狀態不斷變化的過程。（編碼用‘狀態’描述，并且將‘狀態’融入到算法實現中）

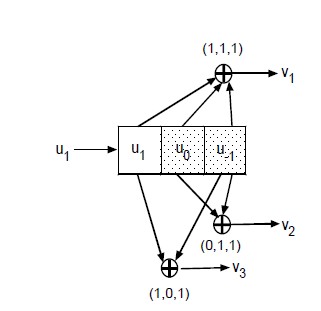
在完成解碼的過程中，找了許多關于Viterbi算法的papers，但在編碼過程對狀態機模型的認識過程中，意識到，解碼過程對狀態機模型的依賴。實際上，Viterbi算法就是一個在狀態機模型基礎上不斷減少可能路徑的一個過程。因為解碼是編碼的一個逆序過程，接受比特和初始狀態是我們已知的信息，我們無法找到一個逆序的算法來計算輸入比特信息。

所以Viterbi算法利用的就是‘重新編碼’的思想，計算每條路徑可能的概率值大小，用概率最大的路徑來模擬編碼過程。從而得到輸入比特信息。而狀態機模型的應用大大提升了解碼過程尋找正確路徑的速度。而在用matlab算法實現的過程中，老師用initial state和next state作為矩陣的行列號，查找輸入比特的速度比我實現時不斷循環查找狀態表提升很多，也使最后所畫的誤碼率對比圖達到理想的接受比特個數（提高了系統的運算能力）。

還記得答辯時候老師問我的那個問題：如果接受比特中錯誤比特的數量一定（假設都是10個），那么錯誤比特均勻分布和集中分布兩種方式哪個誤碼率性能比較好？聽到問題的時候，腦袋想過的編碼過程，錯誤比特的分布情況，所以回答的一塌糊涂。后來才在老師的解釋下，明白了題目的意思。老師想問的是，錯誤比特（信道噪聲影響）的排列分布對解碼時誤碼率性能的影響。卷積碼編碼的時候就假設，每個block是相對獨立的，而瞬時編碼的時候，輸出比特不僅僅與當前的輸入比特信息有關，還與之前的若干blocks里的信息有關（聯合概率）。所以在解碼的時候，每組接收比特的信息也與之前的若干比特信息是相關聯的。

所以，如果誤碼比較集中，在Viterbi時，權值的計算時就會相對增加權值的比重（大的越大，小的越小），容易將該條路徑淘汰。而誤碼分散排列時，一些權值有可能比較接近，無法淘汰。因此誤碼集中分布的情況，系統的誤碼率性能較好。老師的問題，一定程度上又深化了我對整個系統認識的深度。不僅僅在編碼上，而且在解碼端理解卷積碼的意義：用相鄰信息編碼、解碼，使得信息能在信道中準確傳輸。

而拋開狀態機模型的應用，Viterbi算法的關鍵在于路徑選擇的權值（metric）問題。權值的計算的優化能大大提升系統誤碼率的大小。這樣，就到了最后一個問題，硬判決和軟判決對系統誤碼率的提升能力分析。從星座圖的角度看，誤碼率性能體現在是否能夠找到正確的接收比特組合信息，即糾正錯碼的距離（糾正錯碼的能力）。

硬判決在解調時直接將接受比特映射到‘0’，‘1’的星座圖空間上，那么使用漢明距離（100%的概率決定接收比特信息）就可以將接收比特投射到相應的星座圖位置，這樣，如果產生錯碼，硬判決解碼的糾正錯碼的距離將很大（正方形的邊長或對角線）。

而軟判決解調時則在‘0’和‘1’直接設置多個門限，使得接收比特可以投射到范圍內的某個區域里，而通過區域比特的組合信息，使用歐幾何距離（用一定概率值分析接收比特信息）計算最準確的接收比特，這樣，如果產生錯碼，軟判決糾正錯碼的距離將變小（圖b中實點位置，糾正錯碼距離提升），從而得到相對準確的接收比特。因此，軟判決的解碼過程誤碼率性能將優于硬判決。

基于 Vertibi算法的卷積碼解碼設計實現

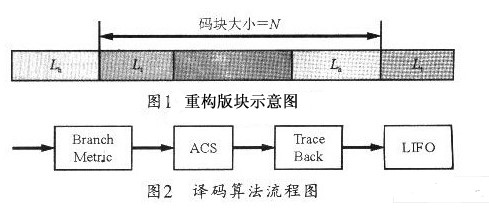
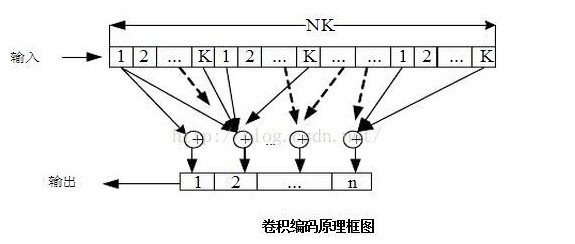
關于Vertibi算法的原理，網上相關的資料很多，況且來看這篇文章的同學對原理應該不陌生，在這里只是簡單提提。我們以（2,1）卷積編碼器為例，其核心可用下面幾幅圖表示

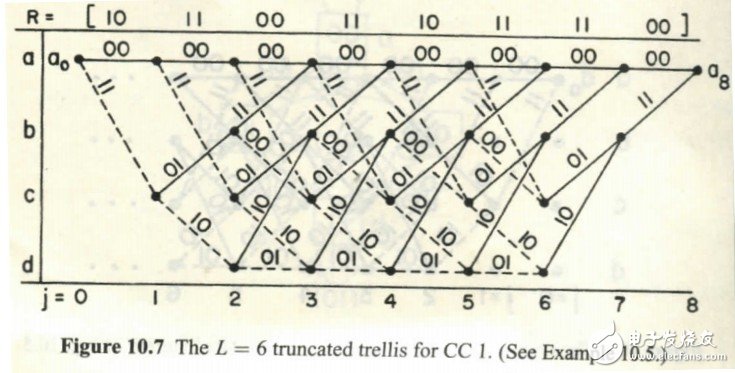
每個卷積編碼器可用狀態轉移來表示，因此圖中a,b,c,d代表編碼器所處的4個狀態，而j表示時刻，實線表示輸入為1，虛線表示輸入為0，而線上的數字表示輸入對應的輸入；打個比方，圖中(a,0)點到(c,1)點的連接表示：當輸入為0時，寄存器的狀態從0時刻的a（我們設為兩個寄存器的狀態全為0，記為00）到1時刻的c（記為10），且伴隨著輸出為11

而Vertibi譯碼則是從上圖中找出一條路，使這條路徑對應的輸出序列與輸入序列的漢明距離最小（既“最像”）

面對這種問題，我們首先想到的便是樹的深度遍歷，既找出所有路徑然后看看誰“最像”。然而。Vertibi就是靠這個成為南加州大學知名校友，創立高通公司，并且成功讓系主任花半節課將他的生平，自然有其妙♂處。

請看下圖

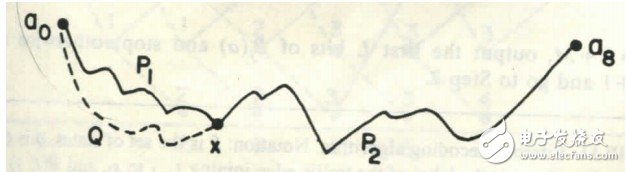
它闡述了一個定理：如果P是最短路徑，對于P上任意一點x，P1一定是最短路徑。
這個定理可以很輕松的用反證法證明

之后的東西好難用語言描述所以我們直接看偽代碼吧

在這里做些解釋

首先定義路徑長度為兩個狀態轉移時的輸出序列與相應的輸入序列的漢明距離

u[j][s]代表J時刻到達s狀態的累計路徑長度

l[t][s]代表從t狀態轉到l狀態的的路徑長度

B[s]代表s狀態的對應解碼序列

由于最后路徑會回到a狀態（既寄存器為00狀態），因此按照以上方法執行后，B(a)即為結果

int vertibi（int *seq， int seqLen， int outnum，int innum，int stat［］［MAXSTAT］， int statRow， int out［］［MAXSTAT］［MAXBLOCK］，int *res ， int *fixed） {

/*seq為輸入序列，seqLen為輸入序列長度，outnum為輸出數（對于（2，1）卷積碼而言為2），innum位輸入數（對于（2，1）卷積碼而言為1），stat為二維的狀態轉移表（比如說，若狀態a轉到狀態c需要輸入1，則stat［1］［3］=1，無法轉移的值設為-1），statRow為狀態轉移表的列數（既狀態數量），out［］［］［］為三維的數組，存儲兩個狀態間轉換時的輸出序列，res為解碼結果序列，fixed為糾正后的輸入序列*/

int u［MAXJ］［MAXSTAT］;

int B［MAXSTAT］［MAXLEN/2］;

int BB［MAXSTAT］［MAXLEN］; /*BB［s］表示s狀態對應的糾正后序列*/

memset（u， 0， sizeof（u））;

memset（B， 0， sizeof（B））;

memset（BB， 0， sizeof（BB））; /*置零*/

for （int j = 0; j 《 statRow; j++） {

if （！j） u［0］［j］ = 0;

else u［0］［j］ = 100;

}

/*因為狀態的起點為狀態a，所以在0時刻除了狀態a（即u［0］［0］）外其它值都設為無窮大（此處定義為100）*/

int curSeq［MAXBLOCK］; //當前用于計算路徑距離的輸入序列段

for （int J = 1; J 《 seqLen/（outnum*innum）; J++） {//此處的J代表時刻

for （int ii = 0; ii 《 outnum*innum; ii++） {

curSeq［ii］ = seq［（J-1）*outnum*innum+ii］;

} //從輸入中取出當前段

for （int i = 0; i 《 statRow; i++） { //遍歷J時刻的狀態

int min = 100;

int minj = 0; //記錄下保留路徑的起點

for （int j = 0; j 《 statRow; j++） { //遍歷J-1時刻的狀態

int l=0;

for （int jj = 0; jj 《 outnum*innum; jj++） { //遍歷當前段的每個字符來計算路徑距離

if （stat［j］［i］ 《 0） { //若兩個狀態本來就無轉移關系，則將l設為無窮大，這樣這條路徑就不可能被選擇了

l = 100;

break;

}

if （curSeq［jj］ ！= out［j］［i］［jj］） //計算漢明距離

l++;

}

if （（u［J - 1］［j］ + l） 《 min） { min = u［J - 1］［j］ + l; minj = j; } //選出累計路徑長度最小的

}

u［J］［i］ = min; //將最小的累計路徑賦給J時刻的i狀態

for （int ii = 0; ii 《 （J - 1） *outnum* innum; ii++） {

BB［i］［ii］ = BB［minj］［ii］;

}

for （int jj = 0; jj 《 outnum*innum; jj++） {

BB［i］［（J - 1）*outnum*innum + jj］ = out［minj］［i］［jj］;

}

//上面兩個for循環實現從狀態minj繼承糾正序列，再往上面填上對應于當前段的糾正段

for （int ii = 0; ii 《 （J - 1） * innum; ii++） {

B［i］［ii］ = B［minj］［ii］;

}

for （int jj = 0; jj 《 innum; jj++） {

B［i］［（J - 1）*innum + jj］ = stat［minj］［i］;

}

//尾加對應于糾正段的輸入段，原理同上

}

}

for （int i = 0; i 《 seqLen/outnum; i++） {

res［i］ = B［0］［i］;

}

for （int i = 0; i 《 seqLen; i++） {

fixed［i］ = BB［0］［i］;

}

//賦值給res和fixed

return 1;

}

結語

關于Vertibi算法的卷積碼解碼設計應用介紹就到這了，如有不足之處歡迎指正。

相關閱讀推薦：什么是卷積碼

相關閱讀推薦：什么是卷積