特勒根定理概述
兩個拓撲結構相同的集總參數電路中各對應的電流、電壓的乘積之和為零。1952年由B.H.特勒根提出。定理指出,若兩個集總參數電路(電路本身最大線性尺寸遠小于電路中電流或電壓的波長)1和2具有相同的有向圖,并且二者的支路電壓和支路電流分別滿足基爾霍夫定律,則恒有:
式中Uk和Ik分別是電路1的支路電壓和支路電流,ǔk和ǐk分別是電路2的支路電壓和支路電流,b為兩個電路的支路數。兩式的兩組支路電流和支路電壓也可以是同一電路中不同狀態下的兩組電流和電壓(各表示一種工作狀態)。若將上式中的ǔk和ǐk都換成Uk和Ik(這相當于式中支路電流和支路電壓都用同一電路中同一狀態的支路電流和支路電壓),則有ǐ1*ǔ1+ǐ2*ǔ2+···+ǐb*ǔb=0以及I1*U1+I2*U2+···+Ib*Ub=0,即定理2的形式簡化為定理1。
特勒根功率定理
對于一個具有 n 個節點和 b 條支路的電路,假設各支路電流與電壓取關聯參考方向,表示為:i1、u1 , i2、u2 , …… ,ib、ub,則在任何時刻 t ,有:
特勒根功率定理的實質是:功率守恒。這是一個普適定理,因此,它適用于一切集總電路,而不管它是線性的、非線性的、時變的、時不變的。
以特例來證明:
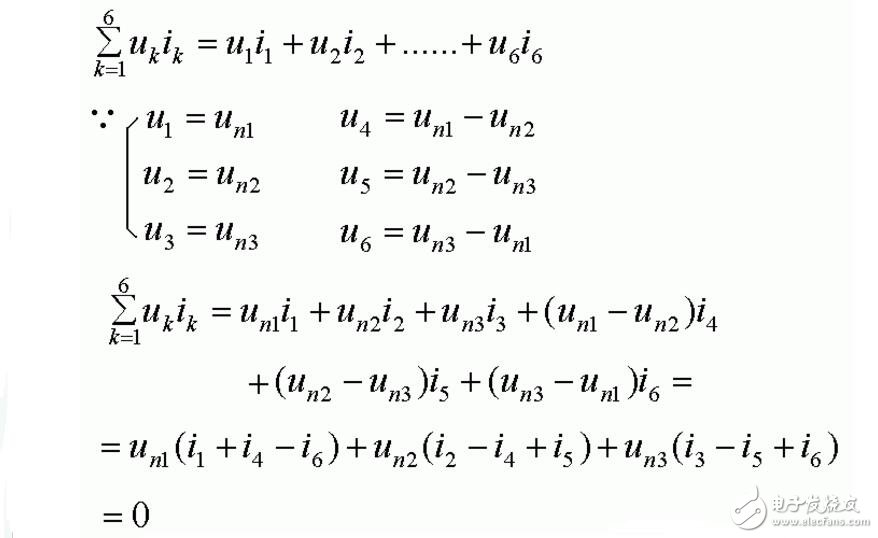
特勒根似功率定理
有兩個電路,假設它們的節點數、支路總數相同,圖也相同,支路上的元件可以不同。并假定各支路電流和電壓取關聯參考方向,則兩電路對應支路電壓和電流的交叉乘積代數和為零:

證明與上述類似,此處從略。
該定理描述的是兩個具有相同拓撲結構的電路,其電壓電流之間滿足的一個數學關系式,沒有具體的物理含義,因此稱為 “ 似功率定理 ”。
特勒根定理作用
應用特勒根定理可方便地證明電路中的互易定理、復功率平衡定理等。
特勒根定理1明確反映了電路實際功率的守恒。但特勒根定理2曾僅僅被認為只有功率守恒的數學形式,卻無法與實際電路對應,因此定理2也被稱為“擬功率定理”。定理2后也被證明反映了電路實際功率的守恒,并具有共軛性。
-
拓撲結構
+關注
關注
6文章
325瀏覽量
39313 -
支路
+關注
關注
0文章
8瀏覽量
7176 -
定理
+關注
關注
0文章
7瀏覽量
7724
發布評論請先 登錄
相關推薦
科勒能源正式更名為瑞勒科
請問怎么理解DAC1280的比特流?
CAP 定理:理論、實踐
受控電壓源在戴維南定理中的應用
疊加定理時受控源怎么處理
疊加定理電壓源和電流源怎么處理
疊加定理電壓源短路的處理
疊加定理電壓源單獨作用時電流源代表什么
戴維南和諾頓定理的適用條件
戴維南和諾頓定理的應用場合
戴維南和諾頓定理適用于什么電路
布勒集團任命何軍慧女士為大中華區總裁





 特勒根定理如何理解
特勒根定理如何理解










評論