編者按:Databricks數(shù)據(jù)科學(xué)主管Sean Owen介紹了常見概率分布背后的直覺及相互聯(lián)系。
數(shù)據(jù)科學(xué),不管它到底是什么,其影響力已不可忽視。“數(shù)據(jù)科學(xué)家比任何軟件工程師都更擅長統(tǒng)計(jì)學(xué)。”你可能在本地的技術(shù)聚會(huì)或者黑客松上無意中聽到一個(gè)專家這么說。應(yīng)用數(shù)學(xué)家大仇得報(bào),畢竟從咆哮的二十年代起人們就不怎么談?wù)摻y(tǒng)計(jì)學(xué)了。以前聊天的時(shí)候,像你這樣的工程師,會(huì)因?yàn)榉治鰩煆膩頉]聽說過Apache Bikeshed(口水仗)這個(gè)分布式評(píng)論格式編排項(xiàng)目而發(fā)出嘖嘖聲。現(xiàn)在,你卻突然發(fā)現(xiàn)人們?cè)诹闹眯艆^(qū)間的時(shí)候不帶上你了。為了融入聊天,為了重新成為聚會(huì)的靈魂人物,你需要惡補(bǔ)下統(tǒng)計(jì)學(xué)。不用學(xué)到正確理解的程度,只需學(xué)到讓人們(基于基本的觀測(cè))覺得你可能理解了的程度。
數(shù)據(jù)科學(xué)文氏圖
正如數(shù)據(jù)結(jié)構(gòu)是計(jì)算機(jī)科學(xué)的基礎(chǔ),概率分布是統(tǒng)計(jì)學(xué)的基礎(chǔ)。如果你計(jì)劃像一個(gè)數(shù)據(jù)科學(xué)家一樣聊天,那么概率分布就是你學(xué)習(xí)的起點(diǎn)。有時(shí)候,不怎么理解概率分布的情況下,使用R或scikit-learn就可以完成一些簡單的分析,就像不理解哈希函數(shù)也可以編寫Java程序一樣。然而,很快你就會(huì)碰到bug和虛假的結(jié)果,并為此痛哭流涕,或者更糟:收獲統(tǒng)計(jì)學(xué)專業(yè)人士的嘆息和白眼。
概率分布有數(shù)百種,有些聽起來像是中世紀(jì)傳說中的怪獸,比如Muth和Lomax。不過,實(shí)踐中經(jīng)常出現(xiàn)的概率分布只有15種。這15種概率分布是什么?關(guān)于它們你需要記憶哪些明智的洞見?請(qǐng)看下文。
什么是概率分布?
每時(shí)每刻都有各種事件正在發(fā)生:骰子擲出、雨滴落下、巴士到站。事件發(fā)生之后,特定的結(jié)果便確定了:擲出3點(diǎn)加4點(diǎn),今日的降雨量是半英寸,巴士3分鐘到站。在事件發(fā)生之前,我們只能討論結(jié)果的可能性。概率分布描述我們對(duì)每種結(jié)果出現(xiàn)概率的想法,有些時(shí)候,我們更關(guān)心概率分布,而不是最可能出現(xiàn)的單個(gè)結(jié)果。概率分布有各種形狀,但大小只有一種:概率分布的概率之和恒等于1.
例如,拋擲一枚勻質(zhì)硬幣有兩種結(jié)果:正面、反面。(假定硬幣落地時(shí)不可能以邊緣立起,或者被空中的海鷗偷走。)在扔硬幣之前,我們相信有二分之一的幾率扔到正面,或者說,0.5的概率。扔到反面的概率同理。這是扔硬幣的兩種結(jié)果的概率分布。實(shí)際上,如果你充分理解了上面的話,那么你已經(jīng)掌握了伯努利分布。
除了奇異的名字之外,常見分布之間的關(guān)系直觀而有趣,所以不管是記憶它們,還是以權(quán)威的語氣評(píng)論它們,都很容易。例如,不少分布都能很自然地從伯努利分布導(dǎo)出。是時(shí)候揭開概率分布的相互關(guān)系地圖了。

常見概率分布及其關(guān)鍵聯(lián)系
上圖中的每種分布都包含相應(yīng)的概率質(zhì)量函數(shù)或概率密度函數(shù)。本文只涉及結(jié)果為單個(gè)數(shù)字的分布,所以橫軸均為可能的數(shù)值結(jié)果的集合。縱軸描述了結(jié)果概率。有些分布是離散的,例如,結(jié)果為0到5之間的整數(shù),其概率質(zhì)量函數(shù)圖形為稀疏的直線,每根線表示一種結(jié)果,線高表示該結(jié)果的概率。有些分布是連續(xù)的,例如,結(jié)果為-1.32到0.005之間的任意實(shí)數(shù),其概率密度函數(shù)為曲線,曲線下的面積表示概率。概率質(zhì)量函數(shù)的線高之和,概率密度函數(shù)的曲線下面積,總是等于1.
把上面這張圖打印出來放到錢包或坤包中。它能指引你厘清概率分布和它們之間的聯(lián)系。
伯努利分布和均勻分布
你已經(jīng)通過上面扔硬幣的例子接觸過伯努利分布了。扔硬幣有兩個(gè)離散的結(jié)果——正面或反面。不過,你可以把結(jié)果看成0(反面)或1(正面)。這兩種結(jié)果發(fā)生的可能性都一樣,如下圖所示。

圖片來源:WolframAlpha
伯努利分布可以表示可能性不同的結(jié)果,例如拋擲一枚不均勻的硬幣。那么,扔到正面的概率就不是0.5,而是不等于0.5的概率p,扔到反面的概率則是1-p. 和很多分布一樣,伯努利分布實(shí)際上是由參數(shù)定義的一系列分布(伯努利分布由p定義)。你可以將“伯努利”想象為“扔(可能不均勻的)硬幣”。
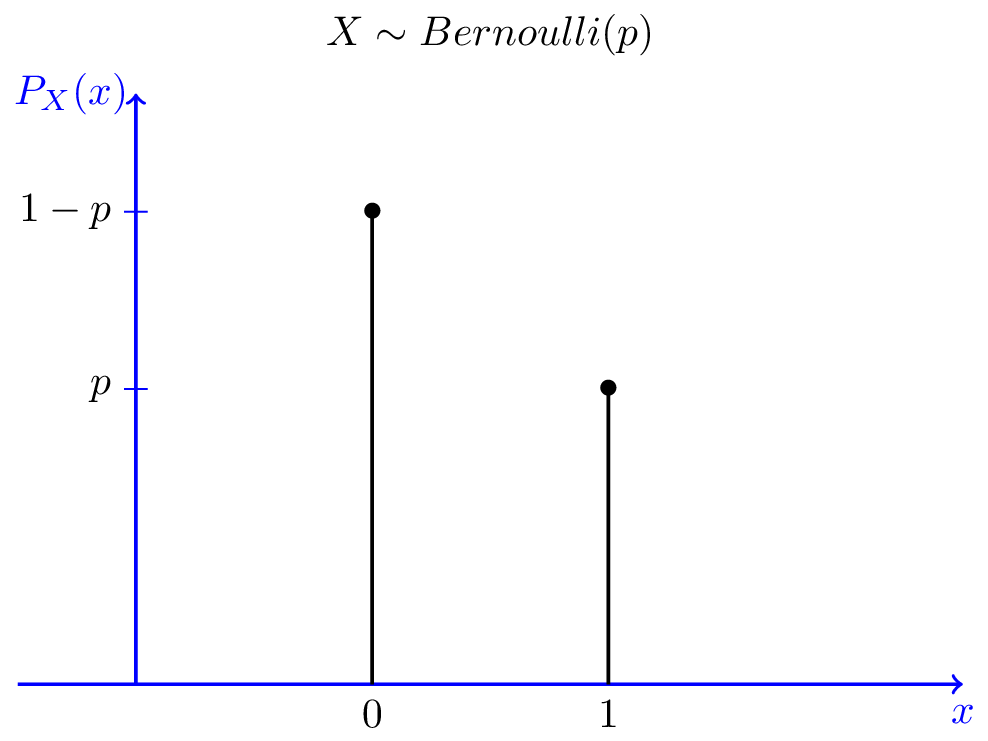
圖片來源:probabilitycourse.com
有多個(gè)結(jié)果,所有結(jié)果發(fā)生概率相等的分布,則是均勻分布。想象拋擲一枚勻質(zhì)骰子,結(jié)果為1點(diǎn)到6點(diǎn),出現(xiàn)每種點(diǎn)數(shù)的可能性相同。均勻分布可以由任意數(shù)目n的結(jié)果定義,甚至可以是連續(xù)分布。
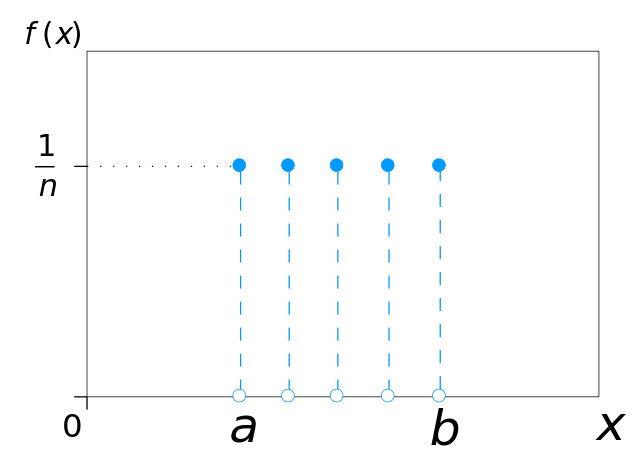
圖片來源:IkamusumeFan;許可: CC BY-SA 3.0
看到均勻分布,就聯(lián)想“投擲一枚均質(zhì)骰子”。
二項(xiàng)分布和超幾何分布
二項(xiàng)分布可以看成遵循伯努利分布的事件的結(jié)果之和。拋擲一枚均質(zhì)硬幣,扔20次,有多少次扔出正面?這一計(jì)數(shù)的結(jié)果遵循二項(xiàng)分布。它的參數(shù)是試驗(yàn)數(shù)n和“成功”(這里的“成功”指正面,或1)的概率p。每次拋擲硬幣得到的是一個(gè)遵循伯努利分布的結(jié)果,也就是一次伯努利試驗(yàn)。累計(jì)類似拋擲硬幣(每次拋擲硬幣的結(jié)果相互獨(dú)立,成功的概率保持不變)的事件的成功次數(shù)時(shí),想想二項(xiàng)分布。
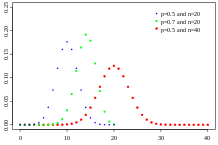
圖片來源:Tayste(公有領(lǐng)域)
或者,你可以想像一個(gè)甕,其中放著數(shù)量相等的白球和黑球。閉上你的眼睛,從甕里抽一個(gè)球,并記錄它是不是黑球,接著把這個(gè)球放回。重復(fù)這一過程。你有多少次抽到黑球?這一計(jì)數(shù)同樣遵循二項(xiàng)分布。
想象這種奇怪的場(chǎng)景是有意義的,因?yàn)檫@讓我們?nèi)菀捉忉尦瑤缀畏植肌T谏厦娴膱?chǎng)景中,如果我們不放回抽取的球,那么結(jié)果計(jì)數(shù)就遵循超幾何分布。毫無疑問,超幾何分布是二項(xiàng)分布的表兄弟,但兩者并不一樣,因?yàn)橐瞥蚝蟪晒Φ母怕矢淖兞恕H绻虻目倲?shù)相對(duì)抽取數(shù)很大,那么這兩個(gè)分布是類似的,因?yàn)殡S著每次抽取,成功的幾率改變很小。
當(dāng)人們談?wù)搹漠Y中抽取球而沒有提到放回時(shí),插上一句“是的,超幾何分布”幾乎總是安全的,因?yàn)槲以诂F(xiàn)實(shí)生活中從來沒碰到任何人真用球裝滿一個(gè)甕,接著從中抽球,然后放回。(我甚至不知道誰擁有一個(gè)甕。)更寬泛的例子,是從種群中抽取顯著的子集作為樣本。
泊松分布
累計(jì)每分鐘呼叫熱線的客戶數(shù)?這聽起來像是二項(xiàng)分布,如果你把每一秒看成一次伯努利試驗(yàn)的話。然而,電力公司知道,停電的時(shí)候,同一秒可能有數(shù)百客戶呼叫。將它看成60000次毫秒級(jí)試驗(yàn)仍然不能解決這個(gè)問題——分割的試驗(yàn)數(shù)越多,發(fā)生1次呼叫的概率就越低,更別說2次或更多呼叫了,但是這個(gè)概率再低,技術(shù)上說,始終不是伯努利試驗(yàn)。然而,如果n趨向于無限,p趨向于0,相當(dāng)于在無窮多個(gè)無窮小的時(shí)間切片上,呼叫概率無窮小,我們就得到了二項(xiàng)分布的極限,泊松分布。
類似二項(xiàng)分布,泊松分布是計(jì)數(shù)的分布——某事件發(fā)生的計(jì)數(shù)。泊松分布的參數(shù)不是概率p和試驗(yàn)次數(shù)n,而是平均發(fā)生率λ(相當(dāng)于np)。試圖累計(jì)連續(xù)事件發(fā)生率,統(tǒng)計(jì)一段時(shí)間內(nèi)某事件的發(fā)生數(shù)時(shí),千萬別忘了考慮泊松分布。
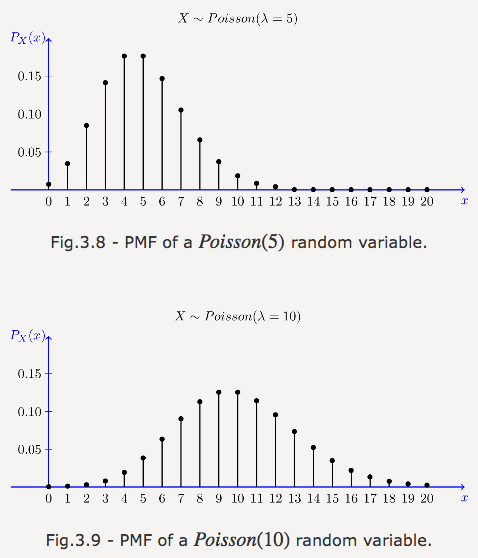
圖片來源:probabilitycourse.com
到達(dá)路由的包、到訪商店的客戶、在某種隊(duì)列中等待的事物,遇到類似這樣的事情,想想“泊松”。
幾何分布和負(fù)二項(xiàng)分布
從伯努利試驗(yàn)又可以引出另一種分布。在第一次出現(xiàn)正面向上之前,扔出了多少次背面向上的硬幣?這一計(jì)數(shù)遵循幾何分布。類似伯努利分布,幾何分布由參數(shù)p(成功概率)決定。幾何分布的參數(shù)不包括試驗(yàn)數(shù)n,因?yàn)榻Y(jié)果本身是失敗的試驗(yàn)數(shù)。

圖片來源:probabilitycourse.com
如果說伯努利分布是“成功了多少次”,那么幾何分布就是“在成功前失敗了多少次”。
負(fù)二項(xiàng)分布是幾何分布的簡單推廣。它是成功r次前失敗的次數(shù)。因此,負(fù)二項(xiàng)分布有一個(gè)額外的參數(shù),r。有時(shí)候,負(fù)二項(xiàng)式分布指r次失敗前成功的次數(shù)。我的人生導(dǎo)師告訴我,成功和失敗取決于你的定義,所以這兩種定義是等價(jià)的(前提是概率p與定義保持一致)。
聊天時(shí),如果你想活躍氣氛,那么可以說,顯然,二項(xiàng)分布和超幾何分布是一對(duì),但是幾何分布和負(fù)二項(xiàng)分布也很類似,接著提問:“我想說,誰起名字起得這么亂?”
指數(shù)分布和威布爾分布
回到客戶支持電話的例子:距下一個(gè)客戶呼叫還有多久?這一等待時(shí)間的分布聽起來像幾何分布,因?yàn)橹钡浇K于有客戶呼叫的那一秒為止,無人呼叫的每一秒可以看成失敗。失敗數(shù)可以視為無人呼叫的秒數(shù),這幾乎是下一次呼叫的等待時(shí)間,但還不夠接近。這次的問題在于,這樣計(jì)算出的等待時(shí)間總是以整秒為單位,沒有計(jì)入客戶最終呼叫的那一秒中的等待時(shí)間。
和之前一樣,對(duì)幾何分布取極限,趨向無窮小的時(shí)間切片,可以奏效。我們得到了指數(shù)分布。指數(shù)分布精確地描述了下一呼叫前的時(shí)間分布。它是一個(gè)連續(xù)分布,因?yàn)榻Y(jié)果不一定是整秒。類似泊松分布,指數(shù)分布由參數(shù)發(fā)生率λ決定。

圖片來源:Skbkekas;許可: CC BY 3.0
和二項(xiàng)分布與幾何分布之間的關(guān)系相呼應(yīng),泊松分布是“給定時(shí)間內(nèi)事件發(fā)生了多少次”,指數(shù)分布則是“直到事件發(fā)生過了多少時(shí)間”。給定一個(gè)某段時(shí)間內(nèi)發(fā)生次數(shù)遵循泊松分布的事件,那么事件間隔時(shí)間遵循參數(shù)λ相同的指數(shù)分布。正是基于這兩種分布之間的這一對(duì)應(yīng)關(guān)系,在談?wù)搩烧咧粫r(shí)提下另一種是很安全的。
涉及“到某事件發(fā)生前的時(shí)間”(也許是“無故障工作時(shí)間”),應(yīng)該考慮指數(shù)分布。實(shí)際上,無故障工作時(shí)間是如此重要,我們有一種更一般的分布對(duì)其加以描述,威布爾分布。指數(shù)分布適用于發(fā)生率(例如,損毀或故障概率)恒定的情況,威布爾分布則可以建模隨著時(shí)間而增加(或減少)的發(fā)生率。指數(shù)分布不過是威布爾分布的一個(gè)特例。
當(dāng)聊天轉(zhuǎn)向無故障工作時(shí)間時(shí),考慮“威布爾”。
正態(tài)分布、對(duì)數(shù)正態(tài)分布、t分布、卡方分布
正態(tài)分布,又稱高斯分布,也許是最重要的概率分布。它的鐘形曲線極具辨識(shí)度。像自然對(duì)數(shù)e一樣,神奇的正態(tài)分布隨處可見。從同一分布大量取樣——任何分布——然后相加,樣本的和遵循(近似的)正態(tài)分布。取樣數(shù)越大,樣本之和就約接近正態(tài)分布。(警告:必須是非病態(tài)分布,必須是獨(dú)立分布,僅僅趨向正態(tài)分布)。無論原分布是何種分布,這一點(diǎn)均成立,真是令人驚奇。
這稱為中心極限定理,你必須知道這個(gè)名詞和它的含義,不然立遭哄笑。
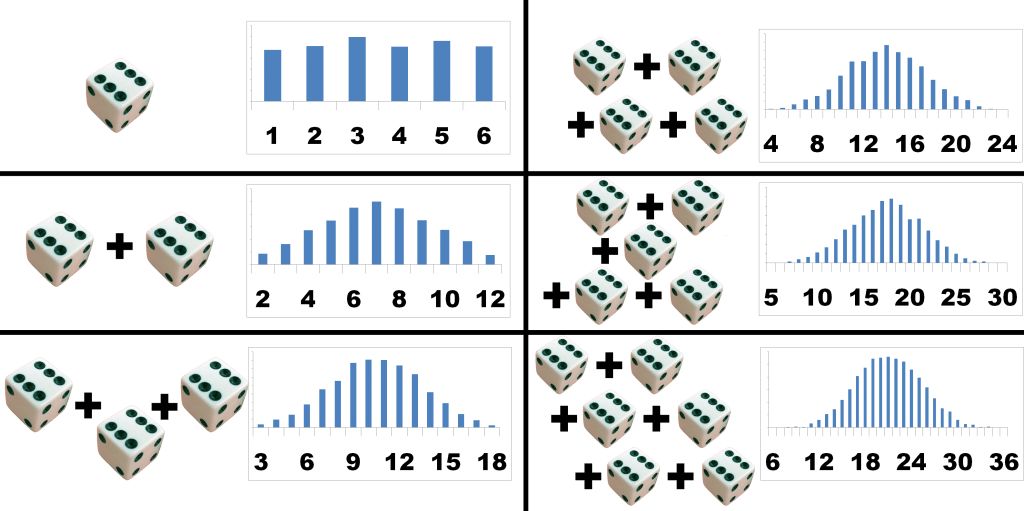
圖片來源:mfviz.com
從這個(gè)意義上說,正態(tài)分布和所有分布相關(guān)。不過,正態(tài)分布和累加尤為相關(guān)。伯努利實(shí)驗(yàn)的和遵循二項(xiàng)分布,隨著試驗(yàn)數(shù)的增加,二項(xiàng)分布變得越來越接近正態(tài)分布。它的表兄弟超幾何分布也是一樣。泊松分布——二項(xiàng)分布的極端形式——也隨著發(fā)生率參數(shù)的增加而逼近正態(tài)分布。
如果對(duì)結(jié)果取對(duì)數(shù),所得遵循正態(tài)分布,那么我們就說結(jié)果遵循對(duì)數(shù)正態(tài)分布。換句話說,正態(tài)分布值的對(duì)數(shù)遵循對(duì)數(shù)正態(tài)分布。如果和遵循正態(tài)分布,那么相應(yīng)的乘積遵循對(duì)數(shù)正態(tài)分布。

圖片來源:維基百科
學(xué)生t-分布是t檢驗(yàn)的基礎(chǔ),許多非統(tǒng)計(jì)學(xué)家在其他學(xué)科中接觸過t檢驗(yàn)。它用于推斷正態(tài)分布的均值,隨著其參數(shù)的增加而更加接近正態(tài)分布。學(xué)生t-分布的主要特點(diǎn)是,尾部比正態(tài)分布更厚(見下圖所示,紅線為學(xué)生t-分布,藍(lán)線為標(biāo)準(zhǔn)正態(tài)分布)。
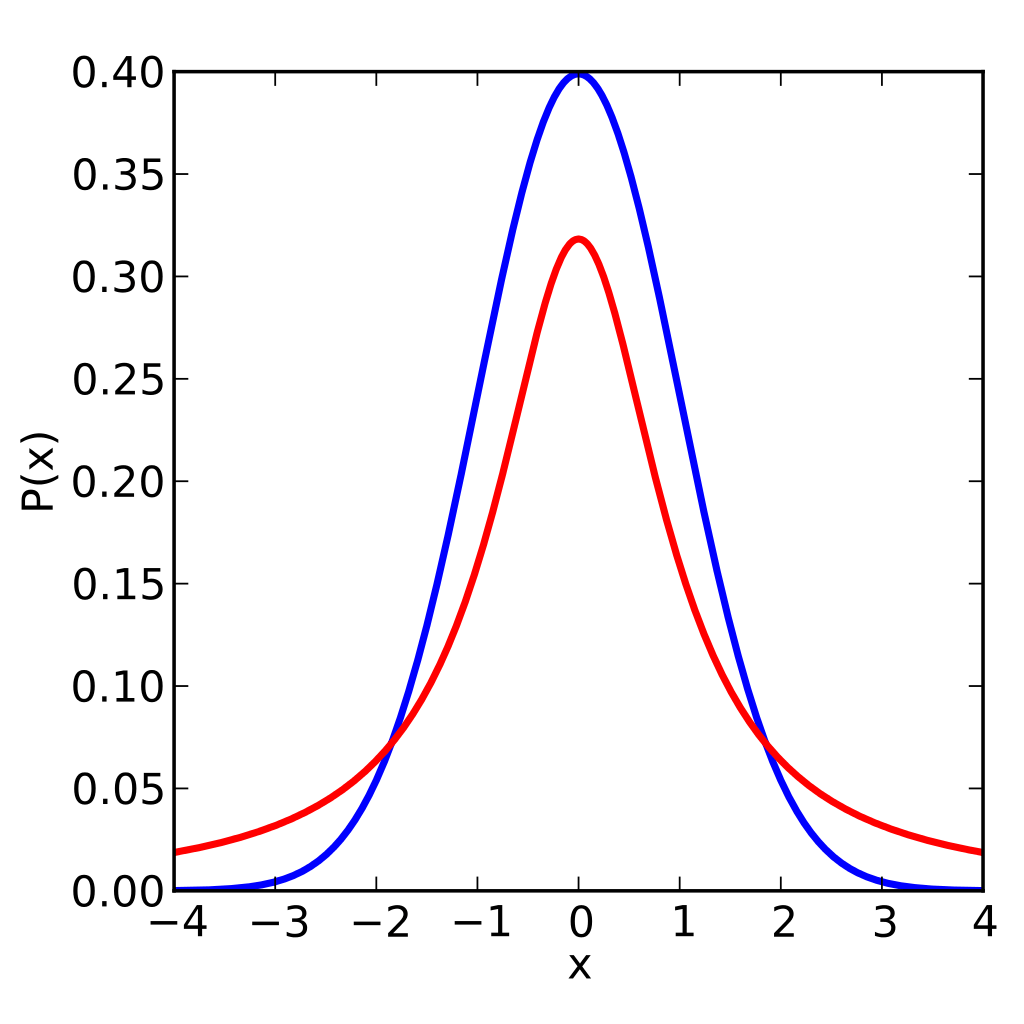
圖片來源:IkamusumeFan;許可: CC BY-SA 3.0
如果厚尾的說法不能引起鄰居的驚嘆,那可以講講比較有趣的和啤酒有關(guān)的背景故事。一百年前,Guinness使用統(tǒng)計(jì)學(xué)釀制更好的烈性黑啤酒。在Guinness,William Sealy Gosset研究出了一種新的統(tǒng)計(jì)學(xué)理論以種出更好的大麥。Gosset說服老板其他釀酒商無法搞明白如何利用這些想法,取得了發(fā)表成果的許可,不過是以筆名“學(xué)生”發(fā)表。Gosset最出名的成果就是學(xué)生t-分布,某種程度上而言是以他的名字命名的。
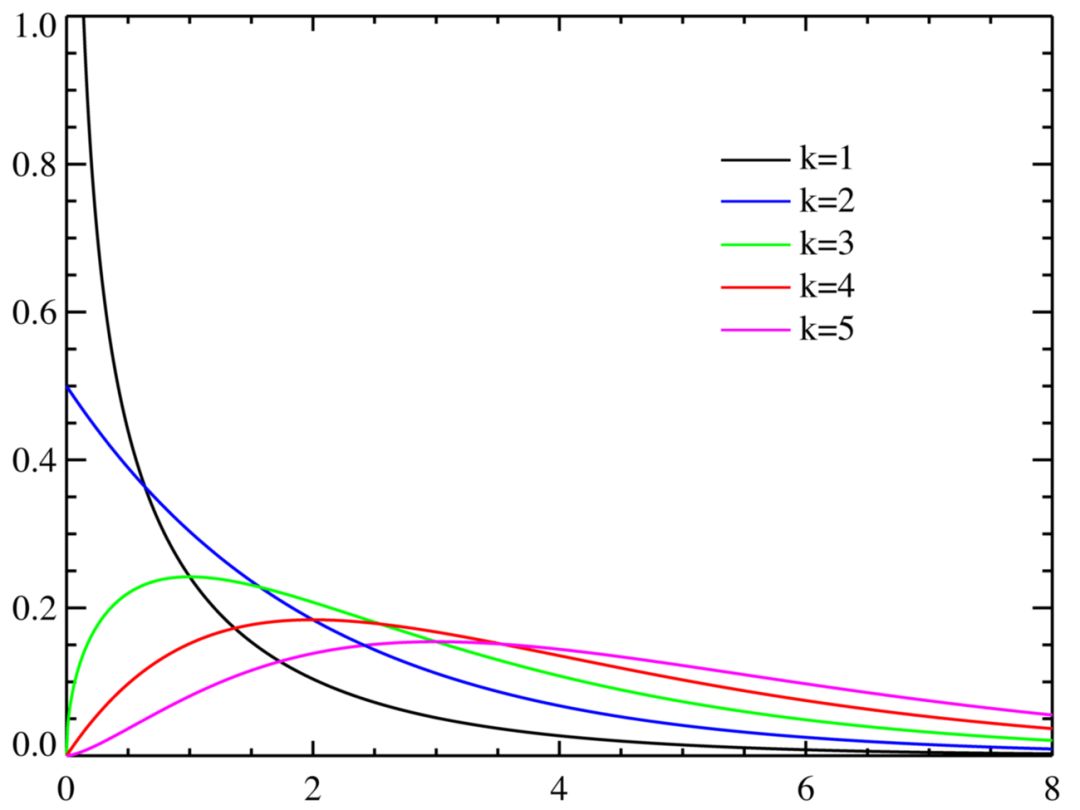
最后,卡方分布是正態(tài)分布值的平方和的分布。它是卡方檢驗(yàn)的基礎(chǔ)。卡方檢驗(yàn)基于觀測(cè)值和理論值的差(假定差遵循正態(tài)分布)的平方和。
伽瑪分布和貝塔分布
如果都談到卡方分布之類了,那么談話應(yīng)該算是比較嚴(yán)肅的。你可能在和真正的統(tǒng)計(jì)學(xué)家聊天,到了這個(gè)份上,你也許該致歉,表示自己知道的不多,因?yàn)橘が敺植贾惖拿~會(huì)出現(xiàn)了。伽瑪分布是指數(shù)分布和卡方分布的推廣。伽瑪分布通常用作等待時(shí)間的復(fù)雜模型,這一點(diǎn)上更像指數(shù)分布。例如,伽瑪分布可以用來建模接下來第n個(gè)事件發(fā)生前的時(shí)間。在機(jī)器學(xué)習(xí)中,伽瑪分布是一些分布的“共軛先驗(yàn)”。
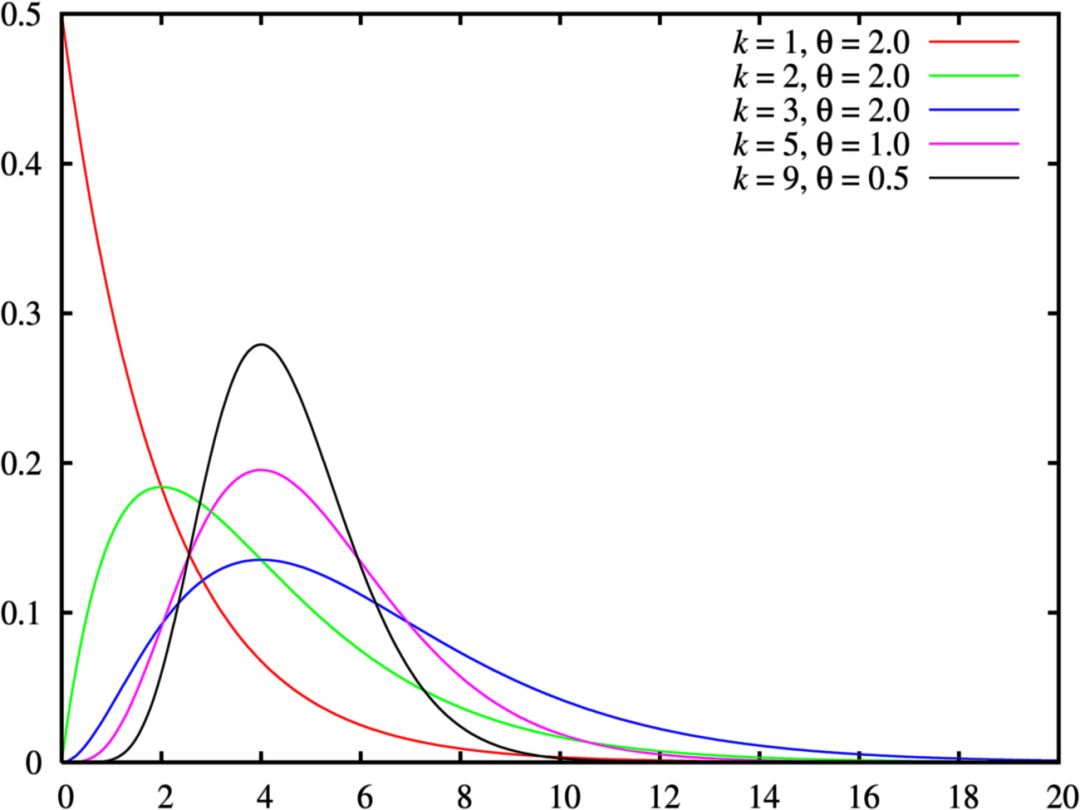
圖片來源:維基百科;許可:GPL
別在共軛先驗(yàn)的對(duì)話中插話,不過如果你真的插話了,準(zhǔn)備好談?wù)撠愃植迹驗(yàn)樗巧厦嫣岬竭^的大多數(shù)分布的共軛先驗(yàn)。就數(shù)據(jù)科學(xué)家而言,貝塔分布的用途主要在此。不經(jīng)意地提到這一點(diǎn),然后朝門口移動(dòng)。

圖片來源:Horas;許可:公有領(lǐng)域
智慧的開端
概率分布的知識(shí)浩如煙海。真正對(duì)概率分布感興趣的可以從下面這張所有單元分布的地圖開始。
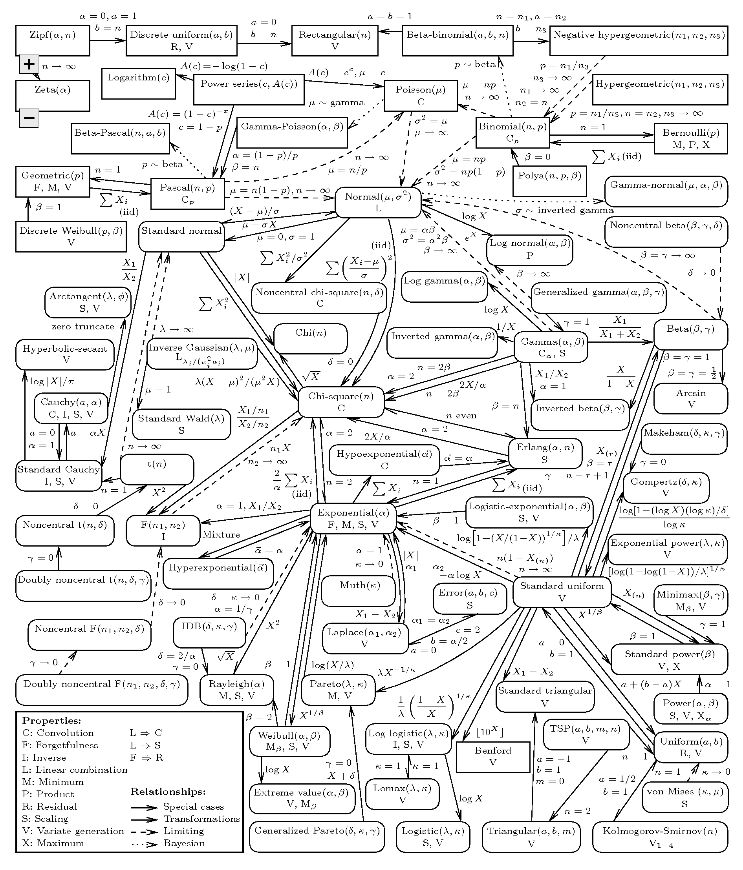
希望本文能給你一點(diǎn)信心,讓自己看起來知識(shí)淵博,并且能融入今日的技術(shù)文化。或者,至少能為你提供一種方法,能夠以很高的概率判斷什么時(shí)候你應(yīng)該找一個(gè)不那么書呆的雞尾酒會(huì)。
-
數(shù)據(jù)結(jié)構(gòu)
+關(guān)注
關(guān)注
3文章
573瀏覽量
40232 -
計(jì)算機(jī)科學(xué)
+關(guān)注
關(guān)注
1文章
144瀏覽量
11403
原文標(biāo)題:常見概率分布的直覺與聯(lián)系
文章出處:【微信號(hào):jqr_AI,微信公眾號(hào):論智】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
基于labview實(shí)現(xiàn)數(shù)據(jù)不同范圍的不同概率分布
概率統(tǒng)計(jì)-怎么對(duì)csv文件進(jìn)行概率密度函數(shù)和累積分布函數(shù)
一種基帶GMSK信號(hào)相關(guān)器及其輸出概率分布
模2n加整體逼近模2 加產(chǎn)生的噪聲函數(shù)的概率分布研究
一種新的基于概率理論的概率數(shù)據(jù)互聯(lián)濾波器
隨機(jī)射線的概率分布及其應(yīng)用
基于Wasserstein距離概率分布模型的非線性降維算法
軟直覺multiplicative集
一種線束內(nèi)串?dāng)_概率分布的預(yù)測(cè)方法
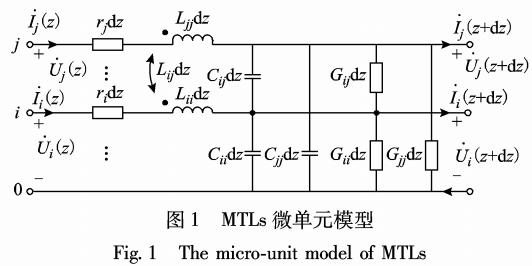
風(fēng)電場(chǎng)群功率波動(dòng)概率密度分布函數(shù)
電網(wǎng)頻率概率分布研究
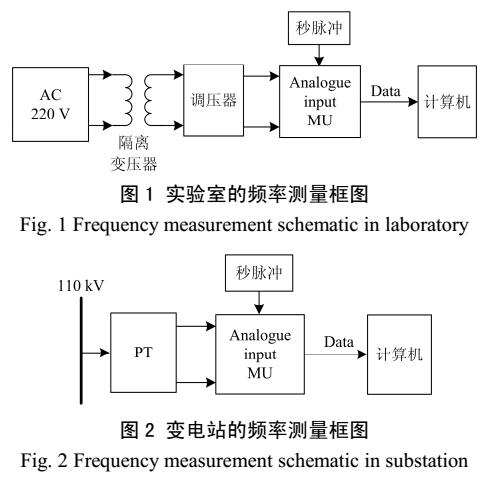
深度學(xué)習(xí)基本概率分布教程
數(shù)字量與模擬量的相互聯(lián)系與用途
防雷接地、防雷工程與防雷檢測(cè)的相互聯(lián)系和作用





 常見概率分布背后的直覺及相互聯(lián)系
常見概率分布背后的直覺及相互聯(lián)系










評(píng)論