統計學和機器學習的真正差別。統計學和機器學習在很多情況下是被混淆的，大部分人其實并不能很好的區分二者。介于此，本文詳解的講解了二者實際的差異，非常有指導意義。

很多人并不能很好的區分統計學和機器學習，因為之間確實有太多的相同之處。目前流行的一種說法是，機器學習和統計學之間的主要區別在于它們的目的：機器學習模型旨在使最準確的預測成為可能；統計模型被設計用于推斷變量之間的關系。

這種說法在技術上來說沒有問題，但它沒有給出特別明確或令人滿意的答案。說機器學習是關于準確的預測，而統計模型設計用于推理幾乎是無意義的陳述，除非你精通這些概念。

因為統計數據和統計模型是不一樣的。統計學是數據的數學研究，沒有數據就無法進行統計；統計模型是數據的模型，用于推斷數據中的關系或創建能夠預測未來值的模型。通常，這兩者是相輔相成的。

實際上，我們需要討論兩件事：首先，統計數據與機器學習有何不同？其次，統計模型與機器學習有何不同。所以今天，我們就來詳細解讀一下二者的區別。

統計學模型與機器學習在線性回歸上的差異

可能因為統計建模和機器學習中使用的方法的相似性，使人們認為它們是同一個東西。可以理解，但根本不是這樣。

最明顯的例子是線性回歸，這可能是造成這種誤解的主要原因。線性回歸是一種統計方法，我們訓練線性回歸量并獲得與統計回歸模型相同的結果，旨在最小化數據點之間的平方誤差。

在一個案例中，我們做了“訓練”模型的事情，其中涉及使用數據的一個子集。我們不知道模型將如何執行，直到在訓練期間能夠“測試”出此數據不存在的、被稱為測試集的其他數據。在這種情況下，機器學習的目的是在測試集上獲得最佳性能。

對于統計模型，我們只要找出可以最小化所有數據的均方誤差（假設數據是一個線性回歸量，加上一些隨機噪聲，本質上通常是高斯噪聲），無需訓練，也無需測試。

一般來說，特別是在研究中（例如下面的傳感器示例），模型的要點是表征數據與結果變量之間的關系，而不是對未來數據進行預測。我們將此過程稱為統計推斷，而不是預測。但我們仍然可以使用此模型進行預測，但評估模型的方式不涉及測試集，而是涉及評估模型參數的重要性和穩健性。

（受監督的）機器學習的目的是獲得可以進行可重復預測的模型。我們通常不關心模型是否可解釋，機器學習只看重結果。而統計建模更多的是發現變量之間的關系和這些關系的重要性，同時也適合預測。

舉例說明這兩個程序之間差異。一名環境科學家主要研究傳感器數據。如果試圖證明傳感器能夠響應某種刺激（例如氣體濃度），就會使用統計模型來確定信號響應是否具有統計顯著性。

他會嘗試理解這種關系并測試其可重復性，以便能夠準確地表征傳感器響應并根據這些數據做出推斷。可能測試的一些事情包括實際上，響應是否是線性的？響應是否可以歸因于氣體濃度而不是傳感器中的隨機噪聲？等等。

而同時，我們還可以獲得20個不同傳感器的陣列，可以用來嘗試預測新近表征的傳感器的響應。我們不認為一個預測傳感器結果的20個不同變量的模型具備多少可解釋性。由于化學動力學和物理變量與氣體濃度之間的關系引起的非線性，這個模型可能會比神經網絡更深奧。我希望這個模型有意義，但只要我能做出準確的預測就已經很不錯了。

如果試圖證明數據變量之間的關系達到一定程度的統計顯著性，那么發論文的時候應該會使用統計模型而不是機器學習。這是因為我們更關心變量之間的關系，而不是做出預測。做出預測仍然很重要，但是大多數機器學習算法缺乏可解釋性使得難以證明數據內的關系（這實際上是學術研究中的一個大問題，研究人員使用他們不理解和獲得的算法似是而非的推論）。

這兩種方法的目標不同，盡管使用的方法類似。機器學習算法的評估使用測試集來驗證其準確性。統計模型可以使用置信區間，顯著性檢驗和其他檢驗對回歸參數進行分析，以評估模型的合法性。由于這些方法產生相同的結果，因此很容易理解為什么人們可能認為它們是相同的。

統計與機器學習在線性回歸上的差異

有一個誤解存在了10年：僅基于它們都利用相同的基本概率概念這一事實，來混淆這兩個術語是不合理的。

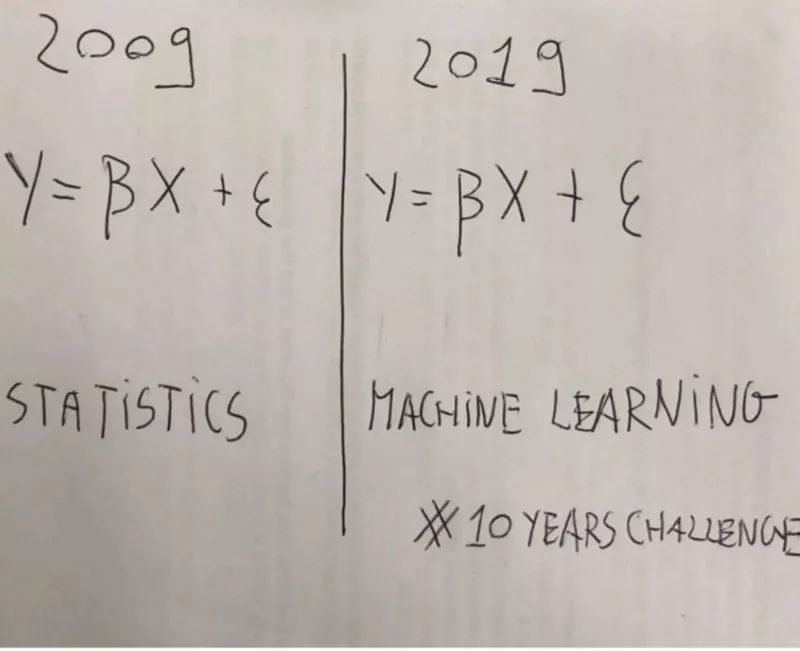
有人一種說法是，根據這個事實做出機器學習只是美化統計的陳述，我們也可以做出以下陳述：

物理學只是美化數學

動物學只是美化郵票收藏

建筑只是美化沙子城堡建筑

這些陳述（尤其是第三個）非常荒謬，所有這些陳述都基于這種混淆基于類似想法的術語的想法（用于架構示例的雙關語）。

實際上，物理學是建立在數學基礎之上的，它是數學應用于理解現實中存在的物理現象。物理學還包括統計學的各個方面，現代統計學的形式通常是由一個由Zermelo-Frankel集理論與測量理論相結合的框架構建，以產生概率空間。它們之間都有很多共同之處，因為都來自相似的起源，并應用類似的想法，來達成合乎邏輯的結論。同樣，建筑和沙堡建筑也有很多共同點啊，但這兩個顯然不是一個概念。

還有兩個與機器學習和統計相關的常見誤解我們需要糾正一下，一個是混淆了數據科學和統計學；另一個是混淆了機器學習和人工智能。這些是AI與機器學習不同，數據科學與統計學不同。這些是相當無爭議的問題所以它會很快。

數據科學 vs 統計學

數據科學本質上是應用于數據的計算和統計方法，這些方法可以是小型或大型數據集，也可以是探索性數據分析。數據被檢查和可視化，以幫助科學家更好地理解數據，并從中做出推論。數據科學還包括數據爭用和預處理等內容，因此還在某種程度上涉及到計算機科學，例如編碼，在數據庫，Web服務器等之間建立連接和pipe等。不一定非得使用計算機來進行統計，但如果沒有計算機，就沒法真正進行數據科學。所以，數據科學使用統計數據，但二者也顯然不一樣。

機器學習 vs 人工智能

機器學習跟人工智能不同。事實上，機器學習是人工智能的一個子集，這是非常明顯的，因為我們正在“訓練”一臺機器，根據以前的數據對某些類型的數據做出可推廣的推斷。

機器學習是基于統計學的

在我們討論統計和機器學習的不同之前，讓我們首先討論相似之處。我們已經在前幾節中對此進行了一些討論。

機器學習建立在統計框架之上。這應該是顯而易見的，因為機器學習涉及數據，并且必須使用統計框架來描述數據。然而，統計力學也擴展到大量粒子的熱力學，也建立在統計框架之上。壓力的概念實際上是一個統計量，溫度也是一個統計量。如果你覺得這聽起來很荒謬可笑，但事實上確實如此。這就是為什么你無法描述分子的溫度或壓力，這是荒謬的。溫度是分子碰撞產生的平均能量的表現。對于足夠大量的分子，我們可以描述像房子或戶外的溫度。

你會承認熱力學和統計學是一樣的嗎？不，熱力學使用統計數據來幫助我們以運輸現象的形式理解工作和熱量的相互作用。

實際上，熱力學是建立在除了統計之外的更多項目之上的。同樣，機器學習也利用了大量其他數學和計算機科學領域，例如：

ML理論來自數學和統計學等領域

ML算法來自優化，矩陣代數，微積分等領域

ML實現來自計算機科學與工程概念（例如內核技巧，特征散列）

當你開始使用Python進行編碼，剔除sklearn庫并開始使用這些算法時，很多這些概念都被抽象出來，因此很難看出這些差異。

統計學習理論：機器學習的統計基礎

統計學與機器學習之間的主要區別在于統計學僅基于概率空間。從集合論中推導出整個統計數據，它討論了我們如何將數字組合成類別，稱為集合，然后對此集合強加一個度量，以確保所有這些的總和值為1，我們稱之為概率空間。

除了這些集合和度量的概念之外，統計數據不對宇宙做任何其他假設。這就是為什么當我們用非常嚴格的數學術語指定概率空間時，我們指定了3個東西。

概率空間，我們這樣表示，（Ω，F，P）由三部分組成：

樣本空間Ω，它是所有可能結果的集合

一組事件F，其中每個事件是包含零個或多個結果的集合

為事件分配概率P; 也就是說，從事件到概率的函數

機器學習基于統計學習理論。它仍然基于概率空間的這種公理概念。該理論是在20世紀60年代發展起來的，并擴展到傳統統計學。

機器學習有幾種類型，這里我們主要講監督學習，因為它是最容易解釋的。

根據監督學習的統計學習理論，一組數據，我們將其表示為S={(x?，y?)}。這是一個有n個數據點的數據集，每個數據點由我們稱之為功能的其他一些值描述，這些值由x提供，并且這些特征由某個函數映射以給出值y。

假如說我們已經有了這些數據，我們的目標是找到將x值映射到y值的函數。可以描述此映射的所有可能函數的集合，稱為假設空間。

要找到這個函數，我們必須讓算法“學會”一些方法來找出解決問題的最佳方法，這個過程由損失函數實現。因此，對于我們所擁有的每個假設（建議函數），需要通過查看其對所有數據的預期風險值來評估該函數的執行情況。

預期風險基本上是損失函數乘以數據概率分布的總和。如果我們知道映射的聯合概率分布，就很容易找到最佳函數。然而，這通常是未知的，因此我們最好的選擇是猜測，然后憑經驗確定損失函數是否更好。我們稱之為經驗風險。

然后，我們可以比較不同的函數，并尋找給出最小預期風險的假設，即假設給出數據上所有假設的最小值（稱為下限）。

然而，該算法具有作弊的傾向，可以通過過度擬合數據來最小化其損失函數。這就是為什么在學習基于訓練集數據的函數之后，該函數需要在測試數據集上進行驗證，驗證用的數據數據不會出現在訓練集中。

顯然，這不是統計學看重的點，因為統計學并不需要最小化經驗風險。選擇最小化經驗風險的函數的學習算法稱為經驗風險最小化。

舉例

以線性回歸的簡單情況為例。在傳統意義上，我們嘗試將某些數據之間的錯誤最小化，以便找到可用于描述數據的函數。在這種情況下，常使用均方誤差。我們將它調整為正負誤差不會相互抵消。然后我們可以以封閉形式的方式求解回歸系數。

如果將損失函數作為均方誤差來執行統計學習理論所支持的經驗風險最小化，最終得到的是與傳統線性回歸分析相同的結果。

這是因為兩種情況是等價的，就像在同一數據上執行最大似然估計也會得到相同的結果一樣。最大似然可以用不同的方式來實現同一目標，但沒有人會說最大似然與線性回歸相同，對吧。

另一個需要注意的是，在傳統的統計方法中，并沒有訓練和測試集的概念。而是用度量來檢查模型的執行方式。雖然評估程序不同，但兩種方法都能夠在統計上給出魯棒的結果。

更進一步，傳統的統計方法提供了最優解，因為解決方案具有封閉形式，它沒有測試任何其它假設并收斂到解決方案。而機器學習方法則是嘗試了一堆不同的模型，收斂到最終假設。

如果我們使用了不同的損失函數，結果就不會收斂。例如，如果我們使用鉸鏈損耗（使用標準梯度下降不可微分，那么就需要其他技術，如近端梯度下降來解決問題），那么結果將不會相同。

當然，可以通過考慮模型的偏差來進行最終比較，比如要求機器學習算法測試線性模型，以及多項式模型，指數模型等，以查看這些假設是否更適合我們的先驗損失函數。

這類似于增加相關的假設空間。在傳統的統計意義上，我們選擇一個模型就可以評估其準確性，但不能自動選擇100個不同模型中的最佳模型。因為模型中總有一些偏差源于最初的算法選擇。這是必要的，因為找到對數據集最佳的任意函數是NP難問題。

結論

沒有統計學就不會存在機器學習，但機器學習在當代非常有用，因為自信息爆炸以來人類，已經產生了大量數據。

在“到底應該選擇機器學習還是統計模型”的問題上，很大程度上取決于目的是什么。如果只是想創建一種能夠高精度地預測住房價格的算法，或者使用數據來確定某人是否可能感染某些類型的疾病，那么機器學習可能是更好的方法；如果試圖證明變量之間的關系或從數據推斷，統計模型可能是更好的方法。

還有就是，即使沒有強大的統計學背景，也仍然可以掌握機器學習并應用在實際問題中。但基本的統計思想還是要有的，以防止模型過度擬合和給出似是而非的推論。

這里推薦幾個不錯的課程，可以讓你對機器學習和統計學有更清晰的認識：

9.520/6.860: Statistical Learning Theory and Applications

http://www.mit.edu/~9.520/fall18/

該課程是以統計學家的角度來闡述機器學習

ECE 543: Statistical Learning Theory

http://maxim.ece.illinois.edu/teaching/spring18/index.html