摘要:本文由畢奧—莎伐定律出發(fā),首先討論了由一定長(zhǎng)度的線電流源和矩形環(huán)流源的磁感應(yīng)強(qiáng)度分布,然后在此基礎(chǔ)上,詳盡的論述了基于體電流源的矩形線圈產(chǎn)生的磁場(chǎng)分布。
關(guān)鍵詞:畢奧—莎伐定律;線圈;磁場(chǎng);磁感應(yīng)強(qiáng)度
中圖分類號(hào):TM55 文獻(xiàn)標(biāo)識(shí)碼:A 文章編號(hào):1006-883X(2003)
一、引言
載流線圈是大量電工設(shè)備中不可缺少的裝置 ,是科學(xué)研究和工程問(wèn)題中最常用的一種磁體,在線圈磁體的設(shè)計(jì)與研制中,常需要計(jì)算線圈的磁場(chǎng)分布。由于工程實(shí)際需要和研究問(wèn)題方便,人們對(duì)軸對(duì)稱線圈進(jìn)行了大量而廣泛的研究,取得了大量成果。在科學(xué)研究和工程設(shè)計(jì)中,矩形線圈的應(yīng)用也是相當(dāng)廣泛的,但人們對(duì)矩形線圈的研究卻很少,僅研究了長(zhǎng)方形載流導(dǎo)體的磁場(chǎng)計(jì)算問(wèn)題 ,而未真正涉及矩形線圈的磁場(chǎng)計(jì)算。
為了實(shí)現(xiàn)對(duì)弱磁場(chǎng)或者對(duì)不均勻磁場(chǎng)的測(cè)量,都需要一個(gè)激勵(lì)源,以產(chǎn)生在一定體積范圍內(nèi)具有一定磁場(chǎng)強(qiáng)度(一般為幾個(gè)nT到0.1mT)的勻強(qiáng)磁場(chǎng)。在實(shí)際運(yùn)用中,用于產(chǎn)生勻強(qiáng)的裝置很多,如螺線管、Helmholtz線圈、矩形線圈等,在本文設(shè)計(jì)的無(wú)損檢測(cè)系統(tǒng)采用的是矩形線圈,本文將對(duì)矩形線圈產(chǎn)生勻強(qiáng)磁場(chǎng)的原理及計(jì)算方法進(jìn)行詳盡的分析。
二、具有一定長(zhǎng)度帶電直導(dǎo)線的磁場(chǎng)計(jì)算
根據(jù)畢奧—莎伐定律,空間線電流源產(chǎn)生的磁場(chǎng)強(qiáng)度為:![]() (1)
(1)
式中: B—空間點(diǎn)的磁感應(yīng)強(qiáng)度,其方向垂直于直導(dǎo)線與空間點(diǎn)構(gòu)成的平面;
—真空導(dǎo)磁率(4π10-7T×m/A); I—導(dǎo)線的電流強(qiáng)度; l—導(dǎo)線長(zhǎng)度;
R—源點(diǎn)到場(chǎng)點(diǎn)的距離; eR—R方向的單位矢量。
為了計(jì)算具有一定長(zhǎng)度的電流源在其周圍產(chǎn)生的磁場(chǎng),建立如圖1坐標(biāo)系,并用畢奧—莎伐定律的積分形式:![]() (2)
(2)
電流的方向?yàn)镮i (x方向),場(chǎng)點(diǎn)坐標(biāo)為P(0,0,Z)=Zk,而導(dǎo)線上的點(diǎn)可以表述為(x,Y,0)=xi+Yj,則有![]() 帶入上式,利用
帶入上式,利用 ![]() 計(jì)算可得:
計(jì)算可得:
![]() (3)
(3)
![]() (4)
(4) ![]() (5)
(5) ![]() (6)
(6)
對(duì)于一般的情況而言:
—該空間點(diǎn)到帶電導(dǎo)線的垂直距離,即|PQ|, ![]() ;
;
a—導(dǎo)線底端到該空間點(diǎn)在導(dǎo)線上投影間的距離,即|QA|;
b—導(dǎo)線頂端到該空間點(diǎn)在導(dǎo)線上投影間的距離,即|QB|;
Y— 在XOY平面的投影,即|OQ|;
Z— 在XOZ平面的投影,即|OP|。這樣空間點(diǎn)與其在導(dǎo)線和XOY平面的投影點(diǎn)構(gòu)成一直角三角形△POQ。
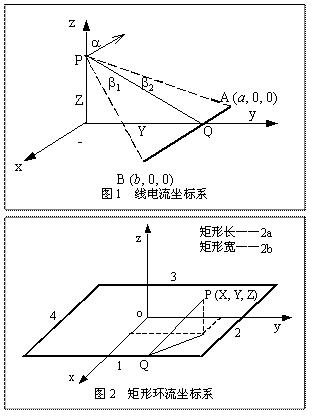
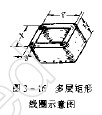
三、矩形環(huán)流的磁場(chǎng)計(jì)算
矩形線圈的每匝相當(dāng)于矩形環(huán)流,因此我們首先分析矩形環(huán)流在空間任意一點(diǎn)的磁感應(yīng)強(qiáng)度的計(jì)算。這里使用疊加原理,即考慮在空間中矩形環(huán)流四條邊(有一定長(zhǎng)度的帶電導(dǎo)線)的疊加效果,從而可得到在Z方向上的磁感應(yīng)強(qiáng)度的矢量和為:
![]() (76)
(76)
式中的B1z、B2z、B3z、B4z分別表示的是矩形線圈四條邊對(duì)空間點(diǎn)產(chǎn)生的Z方向上的磁感應(yīng)強(qiáng)度,也就是由公式(5)推導(dǎo)得到的結(jié)果。對(duì)于1邊產(chǎn)生的磁場(chǎng),首先做出如圖2中的三角形,依據(jù)上一部分的推導(dǎo)可以很容易得到該條邊產(chǎn)生的Z方向的磁感應(yīng)強(qiáng)度,其他幾條邊的推導(dǎo)相同,在此不再贅述。
![]()



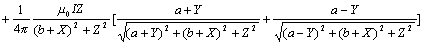 (8)
(8)
式中:I—矩形環(huán)流的通電電流強(qiáng)度;
P—空間點(diǎn),坐標(biāo)為(X,Y,Z);
2a、2b—矩形線圈的長(zhǎng)和寬。
本文設(shè)計(jì)的矩形線圈將用于無(wú)損檢測(cè)的激勵(lì)磁場(chǎng)的產(chǎn)生,因此關(guān)心的是矩形每條邊垂直方向的磁感應(yīng)強(qiáng)度的變化情況,也就是1、3邊將產(chǎn)生的x方向上的磁感應(yīng)強(qiáng)度,以及2、4邊產(chǎn)生的y方向上的磁感應(yīng)強(qiáng)度,因此有以下的結(jié)論:
![]()
![]()
![]()
![]() (9)
(9)
![]()
![]()
![]()
![]() (10)
(10) 
四、矩形線圈磁場(chǎng)的積分計(jì)算
以上對(duì)一定長(zhǎng)度的帶電導(dǎo)線以及矩形環(huán)流在其四周產(chǎn)生的磁感應(yīng)強(qiáng)度進(jìn)行了分析,下面在此基礎(chǔ)上詳盡介紹矩形線圈作為激勵(lì)源產(chǎn)生的磁場(chǎng)分布。為了便于分析,對(duì)矩形線圈建立如圖3的坐標(biāo)系,由體電流源產(chǎn)生的磁感應(yīng)強(qiáng)度,可以通過(guò)下式進(jìn)行計(jì)算:
![]() (11)
(11)
對(duì)于矩形線圈建立的坐標(biāo)系,可以知道,一個(gè)場(chǎng)點(diǎn)的矢量可以表述為: ![]() ,一個(gè)源點(diǎn)的矢量可以表述為
,一個(gè)源點(diǎn)的矢量可以表述為![]() ,空間任意點(diǎn)的磁感應(yīng)強(qiáng)度可以看作是矩形四邊的線圈共同作用的結(jié)果,同樣有以下的結(jié)論:
,空間任意點(diǎn)的磁感應(yīng)強(qiáng)度可以看作是矩形四邊的線圈共同作用的結(jié)果,同樣有以下的結(jié)論: ![]()
對(duì)于區(qū)域1和區(qū)域3只可能產(chǎn)生x、z方向的磁感應(yīng)強(qiáng)度,而區(qū)域2和區(qū)域4只可能產(chǎn)生y、z方向的磁感應(yīng)強(qiáng)度,下面分析區(qū)域1產(chǎn)生的磁場(chǎng)分布:![]()
由(11)式可得:![]()
![]()
![]()
![]()
![]() (12)
(12)
其中: ![]() ;
; ![]()
在這里考慮的是矩形線圈,線圈的厚度相同,因此這里k1=1,其它幾個(gè)方向在其周圍產(chǎn)生的磁感應(yīng)強(qiáng)度推導(dǎo)過(guò)程相同,其各自的電流可以分別描述為-Ji,-Jj,Ji,其具體的論證在此就不再贅述,以下就是分析得到的結(jié)果:![]()
![]() (13)
(13)
其中: ![]() ;
; ![]()
另外,對(duì)于區(qū)域3有: ![]()
![]() (14)
(14)
其中: ![]() ;
; ![]()
對(duì)于區(qū)域4有: ![]()
![]() (15)
(15)
其中: ![]() ;
; ![]()
因此對(duì)于空間任意一點(diǎn),在坐標(biāo)軸方向上的磁感應(yīng)強(qiáng)度的分布可以通過(guò)下列計(jì)算式進(jìn)行計(jì)算:
![]()
![]()
![]() (16)
(16)
下面分析y方向上的磁場(chǎng)分布情況:
![]()
![]()
![]() (17)
(17)
矩形線圈的四條邊對(duì)空間的任意一點(diǎn)都會(huì)產(chǎn)生z方向上的磁場(chǎng),因此由下式存在:
![]()
![]()
![]()
![]()
![]() (18)
(18)
下面再介紹一下對(duì)上述(12)、(13)、(14)、(15)式進(jìn)行數(shù)值積分計(jì)算的方法。在此介紹的使用復(fù)化梯形的方法,其積分形式如下: ![]()
對(duì)區(qū)間[a,b]和[c,d]分別選取正整數(shù)m和n,在x軸和y軸上分別有步長(zhǎng): ![]()
用復(fù)化梯形公式計(jì)算 ![]() ,計(jì)算中將x視為常數(shù),有:
,計(jì)算中將x視為常數(shù),有:
![]() (19)
(19)
在將y當(dāng)作常數(shù),在x方向上計(jì)算(19)式,最終可得到下面的結(jié)論:
![]()
![]()
![]()
![]() (20)
(20)
由分析可知,積分區(qū)域的4個(gè)角點(diǎn)的系數(shù)是1/4,4個(gè)邊界的系數(shù)是1/2,內(nèi)部的節(jié)點(diǎn)的系數(shù)是1,積分結(jié)果的誤差可以通過(guò)下式得到:![]() (21)
(21)
其中 ![]() 和
和 ![]() 在積分區(qū)間內(nèi)。
在積分區(qū)間內(nèi)。
五、總結(jié)
本文從畢奧—莎伐定律關(guān)于計(jì)算線電流源、體電流源的理論出發(fā),由簡(jiǎn)入深的討論了矩形線圈的磁場(chǎng)的理論分析和計(jì)算,并通過(guò)實(shí)際模型的測(cè)試,證明了本文的數(shù)值計(jì)算方法是行之有效的,也對(duì)進(jìn)行矩形線圈的設(shè)計(jì)提供了思路。
- 組圖矩形(5278)
- 磁場(chǎng)分析(5518)
相關(guān)推薦
線圈耦合是什么意思
 310
310磁場(chǎng)線圈的零件維護(hù)
 111
111磁場(chǎng)線圈的電流量是由什么控制
 152
152亥姆霍茲線圈實(shí)驗(yàn)?zāi)康募皩?shí)驗(yàn)原理
 350
350磁場(chǎng)線圈概述
 354
354利用三相交流和線圈制造旋轉(zhuǎn)磁場(chǎng)的方法
 620
620
怎樣選擇磁場(chǎng)發(fā)生器
 234
234
一維圓形亥姆霍茲線圈的不同型號(hào)及技術(shù)指標(biāo)概述
 224
224
亥姆霍茲線圈的實(shí)驗(yàn)?zāi)康募霸?/a>
 815
815
亥姆霍茲線圈的磁場(chǎng)測(cè)量
各種激勵(lì)信號(hào)的對(duì)比與選擇
 3928
3928
高壓放大器在通電空心線圈的脈沖磁場(chǎng)分析中的應(yīng)用
 174
174
線圈模板創(chuàng)建分布式繞組線圈的方法
 1082
1082平面式電感位置傳感器是什么原理?
 2864
2864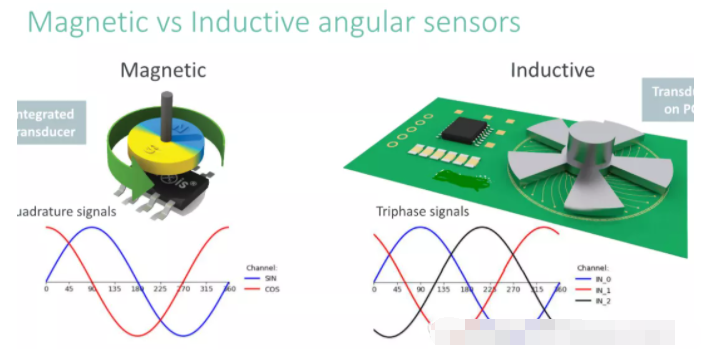
亥姆霍茲線圈全新供電解決方案
 2620
2620功率放大器在線圈電流互感器的研究中的應(yīng)用
 19
19如何讓高頻亥姆霍茲線圈產(chǎn)生強(qiáng)磁場(chǎng)
 5
5采用勵(lì)磁線圈驅(qū)動(dòng)方法實(shí)現(xiàn)外磁場(chǎng)驅(qū)動(dòng)軸流式血泵系統(tǒng)的設(shè)計(jì)
 1943
1943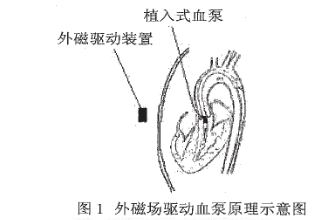
點(diǎn)火線圈的作用_點(diǎn)火線圈正確使用
 8671
8671特斯拉線圈的制作教程
 36227
36227變壓器線圈作用是什么_如何計(jì)算變壓器線圈
 9489
9489高速永磁同步電機(jī)線圈與繞組電樞磁場(chǎng)計(jì)算方法
 0
0基于FPGA的交流電磁場(chǎng)檢測(cè)儀的激勵(lì)源設(shè)計(jì)
 4496
4496
高均勻度磁場(chǎng)線圈的設(shè)計(jì)
 11
11矩形波導(dǎo)中電磁場(chǎng)分布特征研究
 70
70半旋轉(zhuǎn)磁通激勵(lì)的變壓器總損耗分析
 12
12脈沖強(qiáng)磁場(chǎng)裝置原理分析及仿真
 39
39Rogowski線圈的設(shè)計(jì)原理及其預(yù)處理電路的分析
 35
35矩形磁滯回線磁芯
 37
37差動(dòng)變壓器的誤差因素分析
 6788
6788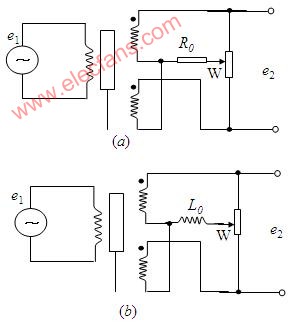
磁場(chǎng)的描繪
 25
25磁場(chǎng)的描繪和研究
 36
3616單元矩形徑向線螺旋陣列天線的理論分析和數(shù)值模擬
 20
20可控硅整流器簡(jiǎn)化開了單穩(wěn)態(tài)線圈激勵(lì)器電路圖
 448
448
磁致伸縮微小驅(qū)動(dòng)器驅(qū)動(dòng)電磁線圈的設(shè)計(jì)研究
 56
56用集成霍爾傳感器探測(cè)亥姆霍茲線圈的交直流磁場(chǎng)
 21
21激勵(lì)頻率對(duì)電感傳感器的影響
 2978
2978
 電子發(fā)燒友App
電子發(fā)燒友App



















評(píng)論