介紹

分治法是計算機科學中很重要的一種思想。英文為Divide and Conquer，直譯即為分治，或者分而治之。直觀的理解就是將一個大而難的問題分解為一些小而易的問題，先解決這些易于解決的小問題，再合并這些小問題的解（合并可以是分別求出小問題的解再合并，或者是直接將相同的小問題合并只求解一次），從而得到大問題的解。需要注意的是小問題必須和大問題是同一個類型的問題，或者說解法相同，這樣才可以遞歸求解。我們發現，這種實際上是自頂向下地分解問題。

我們可以說分治思想是被極廣泛運用的思想。
很多算法和數據結構采用了這種思想。另外計算機圖像渲染將像素點分配給GPU內的多個流處理器分別處理，最后合成出一幀的圖像；也會將一個矩陣乘法分解成n個部分分配給n個處理器并行處理。

下面介紹一些采用了分治思想的算法和數據結構。

算法

快速排序
數列每次按小于某個數（可能是數列的首尾元素或者是隨機選擇或者是三值取中法等）的和大于某個數的標準劃分為兩個子序列，但子序列內的順序和在原數列內的順序一樣，時間復雜度期望nlogn

歸并排序
將數列從中間切成兩半，分別遞歸解決兩半的排序問題，再合并解，即合并兩個有序數列，由于每次合并需要花費O(n)的時間，因此時間復雜度為O(nlogn)。

為了能更好地理解分治的思想，我們詳細介紹一下歸并排序。
比如我們定義mergeSort(array: list, from: int, to: int)為歸并排序函數，那么我們可以這么寫：

join(a: list, b) =if(either a or b is empty) b or aelseif(a[1] < b[1]) [a[1]] + join(a[2:], b)else[b[1]] + join(a, b[2:])mergeSort(array) = join(mergeSort(array[1:mid]), mergeSort(array[mid+1:]))wheremid = length(array) /2

join函數表示合并兩個有序數列，復雜度為O(n)，意思就是有兩個指針i和j一開始分別指向a和b的首元素。這是i和j之前的元素都已經被檢查過了，如果a[i] mergeSort函數就是歸并排序了，我們取中點均分了數列array到array[1..mid]和array[mid+1..n]，兩個子序列經過mergeSort后就是有序的了，這時我們花費O(n)的時間就可以合并兩個有序數列，而不需要再像選擇排序那樣每次都找一遍最值。
如果我們在紙上畫出遞歸的過程：

|---------------| |0000| |---------------| |11|22| |-------|-------| |3|4|5|6| |---|---|---|---|

數字表示遞歸方法的節點編號。
遞歸的層數最多是log2n，對于每個元素都被訪問了O(log2n)次，因此時間復雜度為O(nlogn)。

到這里讀者可能會想到log的底（或者是每次劃分的子問題個數）是不是越大越好呢？顯然不是，應該與實際問題相適應。如果劃分的子問題數過多，那么合并子問題的時候就會導致麻煩。比如歸并排序的有序數列合并，我們之前認為的O(n)的合并是基于劃分2次的。如果我們令劃分的子序列數為b，那么最終的時間復雜度是O(bnlogbn)。我們將其可以寫成

O(nlnnblnb)

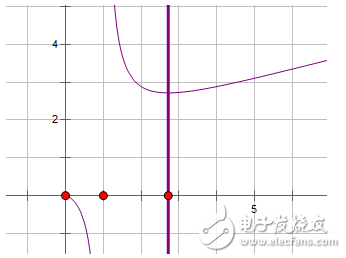
我們發現blnb的最小值點為x=e，也就在2~3之間，而且x=2和x=3的函數值相差不大，也就是說我們劃分成2個子問題或者劃分成3個子問題的時候，效率是最高的。另一方面，劃分成2個子問題的程序比3個的要更好實現，因此我們一般在分治的時候將問題劃分為2個子問題。當然在必要時可能會有其他劃分方法。

快速傅里葉變換
處理多項式的乘法，分解多項式并應用復數的對稱和周期性減少重復計算

快速冪
將求n次冪分為2個n/2次冪的較小問題，而兩個小問題是相同的，求出一個就知道另外一個的解

（在樹上的分治）

……

數據結構

實際上很多基于樹的數據結構都可以認為采用了分治思想，但分治不代表一定是簡單的二分。

線段樹
數列每次對半切割，區間查找被劃分為幾個已有的線段樹節點的并。

線段樹是最基礎的數據結構之一，這里較詳細地講一下。譬如給定一個數列1, 2, 3, 4，構造這個數列的線段樹。
結果如下：

|---------------|| 1 2 3 4 ||---------------|| 1 2 | 3 4 ||---------------|| 1 | 2 | 3 | 4 ||---------------|

看起來和歸并排序的遞歸過程很像。實際上因為都有分治思想，像是必然的。
那么我們查詢區間[2,3]的和，我們會這么走：
[2,3] in [1,4]->[2,2] in [1,2] & [3,3] in [3,4] -> [2,2] in [2,2] & [3,3] in [3,4]
也就是我們將這個區間按照適當的方式（按照已有的劃分方法）劃分成2個子區間（或者正好不需要劃分，繼續往下走），得到2個子區間（子問題）的和，再加起來，得到當前區間（大問題）的和。我們很容易知道，這么做的時間復雜度是均攤logn的。

對半劃分子問題的優勢我們在將歸并排序的時候已經講過了，這里的理由類似。但是像B樹等就不是對半劃分的。
- 伸展樹
數列每次從某個點切割，某個點可以代表一個區間
- 劃分樹
數列每次按較小的一半和較大的一般切割
- 樹狀數組
和線段樹類似
- ……

一些題目

以下題目分類僅供參考。。

分治 POJ

2083

BZOJ

1095, 2001, 2229, 2287, 2458, 2229, 3614, 3658, 3879, 4025, 4059

CodeForces

321E, 576E

樹分治 POJ

1741, 1987, 2114,

BZOJ

1095, 1468, 1758, 2152, 2599, 3365, 3435, 3648, 3672, 3697, 3784, 3924, 4012, 4016, 4372

HDU

4812

CDQ分治 BZOJ

1176, 1492, 1537, 2244, 2683, 2716, 2961, 3262, 3295

總結

我們先介紹了分治法是怎么樣的一種思想，并介紹了一些典型（常見）的運用了分治思想的算法和數據結構。我們了解了分治法是如何自頂向下的。實際上現實生活中我們也能見到分治法的運用。我們寫一個策劃，會將策劃的不同環節交給不同的人做，最后總策劃再將各個人做好的各個部分的策劃修改并整合成最終的總策劃。而每個寫子策劃的人又可能將任務繼續下派分發給部門內部多個人員共同完成。可以說，計算機科學中的分治法源于生活。如此重要的思想，我們一定要理解。