引力波的傳播速度有多快

　　引力波如何傳播的

　　以地球如何感受太陽引力為例。一個更確切的圖像是：太陽產生引力波，以光速傳播到地球所在的位置；引力波傳播的同時，也攜帶的另外四個自由度一起傳播；最終在地球所在的位置產生完整的引力場（六個自由度），然后地球感受到這個引力場——當然，也包括牛頓引力勢。

　　所以，即便太陽有一天突然消失了，我們也只是在8分鐘后才看到天黑了；同樣，在8分鐘后才感覺地球突然被甩了出去。

　　麥克斯韋在1865年得到電磁波動方程，12年后赫茲證實電磁波的存在。遺憾的是，廣義相對論誕生100年之后的今天，仍然沒有直接探測到引力波。

　　目前測量引力傳播速度的實驗，通常是觀測太陽、地球、月亮系統的重力變化，實際上只是觀測牛頓引力勢的作用時間。當然，因為牛頓引力勢總是坐在在引力波這輛跑車上，所以也算是間接測量了引力真正的傳播速度。

　　引力波的傳播速度不能超過光速

　　光速是指光波或電磁波在真空或介質中的傳播速度。真空中的光速是目前所發現的自然界物體運動的最大速度。它與觀測者相對于光源的運動速度無關，即相對于光源靜止和運動的慣性系中測到的光速是相同的。物體的質量將隨著速度的增大而增大，當物體的速度接近光速時，它的質量將趨于無窮大，所以有質量的物體達到光速是不可能的。只有靜止質量為零的光子，才始終以光速運動著。光速與任何速度疊加，得到的仍然是光速。速度的合成不遵從經典力學的法則，而遵從相對論的速度合成法則。

　　在物理學中，引力波是指時空彎曲中的漣漪，通過波的形式從輻射源向外傳播，這種波以引力輻射的形式傳輸能量。在1916年，愛因斯坦基于廣義相對論預言了引力波的存在。引力波的存在是廣義相對論洛倫茲不變性的結果，因為它引入了相互作用的傳播速度有限的概念。相比之下，引力波不能夠存在于牛頓的經典引力理論當中，因為牛頓的經典理論假設物質的相互作用傳播是速度無限的。

　　引力波傳播是瞬時的嗎

　　引力波的傳達究竟是否是瞬間呢，很多人都疑難這個，但是答案肯定是否定的。

　　若何引力波的傳達是瞬間的而沒有是光速的話，會導致宇宙中所有引力場的繚亂，譬喻單個年夜行星會由于遠處一個原本距離適中的質量超小星系的引力所孕育發生的潮汐力而破碎。引力場的傳達速率的具有可導致碩大星系外部引力場的一局部小我平衡，倘使速率密切有限小則會導致“等效事理”極限化，前因顯而易見。

　　倘使碩大星系外部所有星體絕對靜止，引力場的傳達速率也就失落去了宏觀意思，但實踐中沒有具有這類碩大星系。

　　引力波也稱重力波，引力波是愛因斯坦狹義絕對論所預言的一種以光速傳達的時空波動，是時空曲率的擾動以行進波的內容向別傳遞的一種體式格局。猶如電荷被放慢時會收回電磁輻射，同樣有質量的物體被放慢時就會收回引力輻射，這是狹義絕對論的一項主要預言。引力波與流膂力學中的重力波很相似，當液體皮相或者外部液團因為密度不同來到原本職位地方，正在重力（gravity force）以及浮力（buoyancy force）的綜協作用下，液團會處于上下震撼以抵達均衡的狀況。即孕育發生波動。引力波則是因為空間質量以及速率的更動導致空間孕育發生的波動。

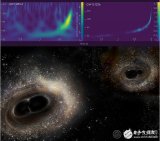
　　LIGO正在2016年2月11日宣告“探測到引力波的具有”。引力波的創造意思重小，從迷信意思上看，引力波可以直截與宇宙小爆炸毗鄰。狹義絕對論中預言的引力波也能夠孕育發生于宇宙小爆炸中，這即是說小爆炸之初的引力波正在137億年后的今日仍舊可以探測到。一旦創造了宇宙小爆炸時代的引力波，就能夠揭開宇宙的各類謎團，以至相識宇宙的初階以及運轉機制。

　　引力波的傳播方向

　　引力波是橫波。首先簡單來說：

　　通常對于有質量的場而言，對應的粒子運動的速度是小于光速的，所以我們總可以找一個和粒子相對靜止的參考系來看問題（Lorentz boost）。 這時粒子的四動量為. 尋找自由度來自于尋找粒子具有的獨立的狀態，來自于尋找在此參考系下，保持此四動量不變的群操作。這個群操作是洛倫茲群的子群。可以看出保持此操作不變的群（也叫little group）是所有空間轉動組成的群也就是SO（3）。 根據高等量子力學的知識，自旋為j的粒子在SO（3）的對稱性下有（2j+1）個自旋態。而對于無質量的場而言，它的運動速度必然是光速，所以無法通過一個boost找到一個和它相對靜止的參考系。這樣四動量最多可以寫成。

　　所以保持此矢量不變的對稱群是ISO（2），可以理解成繞著運動的那個軸的軸對稱群。這時描述它的態只有2個。所以形象的理解就是無質量粒子的縱向的自由度被凍結掉了，留下的只有橫向的自由度，而橫向的自由度對應于經典物理我們通常說它具有橫向的偏振態，所以無論是光子還是引力子都是以光速運動的粒子所以只有2個偏振態，所以都是橫波。其物理的來源在于小群的不同。

　　當然如果懂一點點群論的人而言，還有可以更加清晰的解釋。

　　根據Wigner定理，一種粒子的狀態總是和Poincare群（ 3個轉動，3個洛倫茲變換（boost），4個平移）的表示相聯系的。

　　而在研究群的表示的時候，我們總是喜歡尋找卡西米爾算子，也就是和一個群的所有生成元都對易的算子，這個算子的本征值就是區分有多少種物理粒子態。

　　比如在角動量理論中，角動量的平方就是，，的卡西米爾算子，我們都知道其具有（2j+1）個本征態。

　　而在有質量的場論來說呢？我們的任務也是尋找卡西米爾算子，對于有質量的場論，我們可以找到兩個卡西米爾算子 ， 四動量的平方和泡利魯班斯基矢量的平方。泡利魯班斯基矢量定義說起來有點煩，與自旋關系密切，現在理解成自旋就行。這樣通過這兩個卡西米爾算子的本征值就可以區分粒子態了。的本征值是，關于這一類龐加萊群表示的分類知乎上已經有非常好的回答了。對于特定的，如果粒子具有自旋s，還可以由另外一個卡西米爾算子的本征值分成2s+1個自旋態。一切看上去so far so good.

　　但是如果對于沒有質量的場（電磁場，引力場）， 那么我們就會發現，上面兩個卡西米爾算子的本征值都是0，這樣它們就都不能用了。所以為了給龐加萊群表示分類，我們需要尋找新的洛倫茲不變量，新的洛倫茲不變量就是螺旋度（helicity）， . 也就是自旋在運動方向上的投影。這個卡西米爾算子對于自旋為s的態只具有s，-s兩個本征值，所以只能把它分成兩個狀態，對應于兩個偏振態。于是對于電磁場，引力場等無質量場，只具有橫波自由度了。

　　這時，就會發現這好像和規范對稱性有所聯系了，因為電磁場和引力場之所以自由度被限定成了2個，是因為我們選定了恰當的規范條件。比如電磁場的庫倫規范，關于引力波的規范問題我在我關于引力波的那個回答里也提到過。而且只有無質量場具有規范不變性（關于規范場粒子的質量是來自對稱性破缺），所以也可以把剛才的若干討論看作是規范不變性的起源。

　　注意在量子力學（經典力學）中，規范對稱性通常不認為是對稱性，因為量子力學中物理狀態利用希爾伯特空間的矢量描述，因為規范對稱性相聯系的兩個狀態實際上是相同的，而對稱性描述的兩個狀態是不同的通過對稱性相互聯系。這里通過量子力學來說明，經典力學中同樣規范對稱性也不是對稱性。一個很有誤導性的說法是，電磁場的U（1）整體規范對稱性根據諾特爾定理帶來了電荷守恒，容易讓我們誤導規范對稱性具有守恒流，從而是一個對稱性。實際上這個說法應該改為“整體對稱性根據諾特爾（第一）定理帶來了電荷守恒”，整體對稱性是系統的對稱性而不屬于規范對稱性。

　　延伸閱讀：什么是橫波，如何判斷橫波的方向

　　什么是橫波：橫波的特點是質點的振動方向與波的傳播方向相互垂直。在橫波中波長通常是指相鄰兩個波峰或波谷之間的距離。

　　如何判斷橫波的方向：

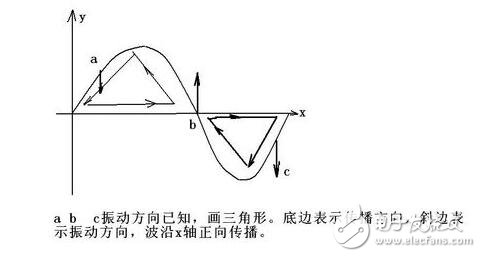
　　知道某點的振動方向，那么傳播方向要么是左要么是右，對吧。看哪個傳播方向與振動方向在波形的同一側，那個就是波的傳播方向。經驗，從來沒判斷錯過。