OPENGL坐標(biāo)系可分為：世界坐標(biāo)系和當(dāng)前繪圖坐標(biāo)系。

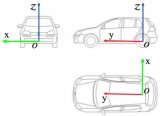
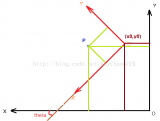
世界坐標(biāo)系：在OpenGL中，世界坐標(biāo)系是以屏幕中心為原點(diǎn)(0, 0, 0)，且是始終不變的。你面對(duì)屏幕，你的右邊是x正軸，上面是y正軸，屏幕指向你的為z正軸。長(zhǎng)度單位這樣來(lái)定：窗口范圍按此單位恰好是(-1,-1)到(1,1)，即屏幕左下角坐標(biāo)為（-1，-1），右上角坐標(biāo)為（1,1）。

當(dāng)前繪圖坐標(biāo)系：是繪制物體時(shí)的坐標(biāo)系。程序剛初始化時(shí)，世界坐標(biāo)系和當(dāng)前繪圖坐標(biāo)系是重合的。當(dāng)用glTranslatef()，glScalef(), glRotatef()等對(duì)當(dāng)前繪圖坐標(biāo)系進(jìn)行平移、伸縮、旋轉(zhuǎn)變換之后，世界坐標(biāo)系和當(dāng)前繪圖坐標(biāo)系不再重合。注意，這里的平移旋轉(zhuǎn)是將當(dāng)前繪圖坐標(biāo)系看做一個(gè)整體在世界坐標(biāo)系中進(jìn)行旋轉(zhuǎn)平移。然后，改變以后，再用glVertex3f()等繪圖函數(shù)繪圖時(shí)，都是在當(dāng)前繪圖坐標(biāo)系進(jìn)行繪圖，所有的函數(shù)參數(shù)也都是相對(duì)當(dāng)前繪圖坐標(biāo)系來(lái)講的。

　　齊次坐標(biāo)

　　只講三維的情況啊

　　向量空間中，只有標(biāo)量和向量

　　向量 + 向量 = 向量

　　標(biāo)量 * 向量 = 向量

　　三維向量空間中，可以視任意一組線性無(wú)關(guān)的向量為基

　　基 V = ［ v1 ， v2 ， v3 ］

　　其他向量可以用一個(gè)三維的元組來(lái)表示

　　向量 a = ［ A1 ， A2 ， A3 ］

　　于是 向量 a = A1 * v2 + A2 * v2 + A3 * v3

　　僅有向量是無(wú)法表示幾何的，至少要有點(diǎn)吧

　　一般認(rèn)為點(diǎn)的表示也是一個(gè)三維的元組

　　點(diǎn) b = ［ B1 ， B2 ， B3 ］

　　這樣就無(wú)法區(qū)分點(diǎn)和向量了，咋辦？

　　仿射空間

　　仿射空間中，基稱為標(biāo)架，由三個(gè)向量和一個(gè)點(diǎn)組成

　　標(biāo)架 V = ［ v1 ， v2 ， v3 ， p ］

　　仿射空間的運(yùn)算

　　向量+ 向量 = 向量

　　標(biāo)量 * 向量 = 向量

　　點(diǎn) + 向量 = 點(diǎn)

　　PS：可以看到，點(diǎn)與向量的和為另一個(gè)點(diǎn)，其實(shí)也可以認(rèn)為向量記錄的是點(diǎn)的運(yùn)動(dòng)，記錄著一個(gè)點(diǎn)轉(zhuǎn)換到另一個(gè)點(diǎn)的信息

　　于是

　　向量 a = ［ a1 ， a2 ， a3 ， 0 ］

　　點(diǎn) b = ［ b1 ， b2 ， b3 ， 1 ］

　　即

　　a = a1 * v1 + a2 * v2 + a3 * v3 ， 確實(shí)是向量

　　b = b1 * v1 + b2 * v2 + b3 * v3 + p

　　b = 向量 + p = 點(diǎn)

　　勉強(qiáng)區(qū)分開(kāi)了哈

　　還有問(wèn)題

　　點(diǎn)p和向量v1v2v3怎么確定？它們的值又是在那種標(biāo)架或基下的？

　　所以討論了再多，這個(gè)標(biāo)架其實(shí)還是對(duì)應(yīng)我們普通的三維坐標(biāo)系才顯得平易近人，即

　　點(diǎn)p為原點(diǎn)

　　v1 v2 v3 分別對(duì)應(yīng)三個(gè)坐標(biāo)軸 ［1，0，0］、［0，1，0］、［0，0，1］

　　只不過(guò)我還告訴你，對(duì)于任意一個(gè)點(diǎn)和任意三個(gè)線性無(wú)關(guān)的向量v1 v2 v3，其都可以當(dāng)作一個(gè)標(biāo)架。因?yàn)槿齻€(gè)線性無(wú)關(guān)的向量就可以表示出任意一個(gè)向量，再有一個(gè)點(diǎn)為基礎(chǔ)，就可以表示任意一個(gè)點(diǎn)

　　所以想OpenGL中就默認(rèn)，其世界坐標(biāo)系對(duì)應(yīng)的仿射空間，p為原點(diǎn)，v1v2v3為坐標(biāo)軸

　　但是相機(jī)坐標(biāo)系就不是了，因?yàn)樯叮恳驗(yàn)橄鄼C(jī)可以移動(dòng)啊，可以改變朝向和正向，這些都影響著相機(jī)坐標(biāo)系。單就移動(dòng)來(lái)說(shuō)：

　　相機(jī)的默認(rèn)位置是在世界坐標(biāo)系的原點(diǎn)，移動(dòng)了之后就不是了啊

　　那么你在相機(jī)的位置看世界坐標(biāo)系上的點(diǎn)，那些點(diǎn)的坐標(biāo)表示就應(yīng)該轉(zhuǎn)換到相機(jī)坐標(biāo)系上來(lái)，才對(duì)應(yīng)著我們真正應(yīng)該看到的點(diǎn)的位置

　　還是寫寫坐標(biāo)系比較實(shí)在

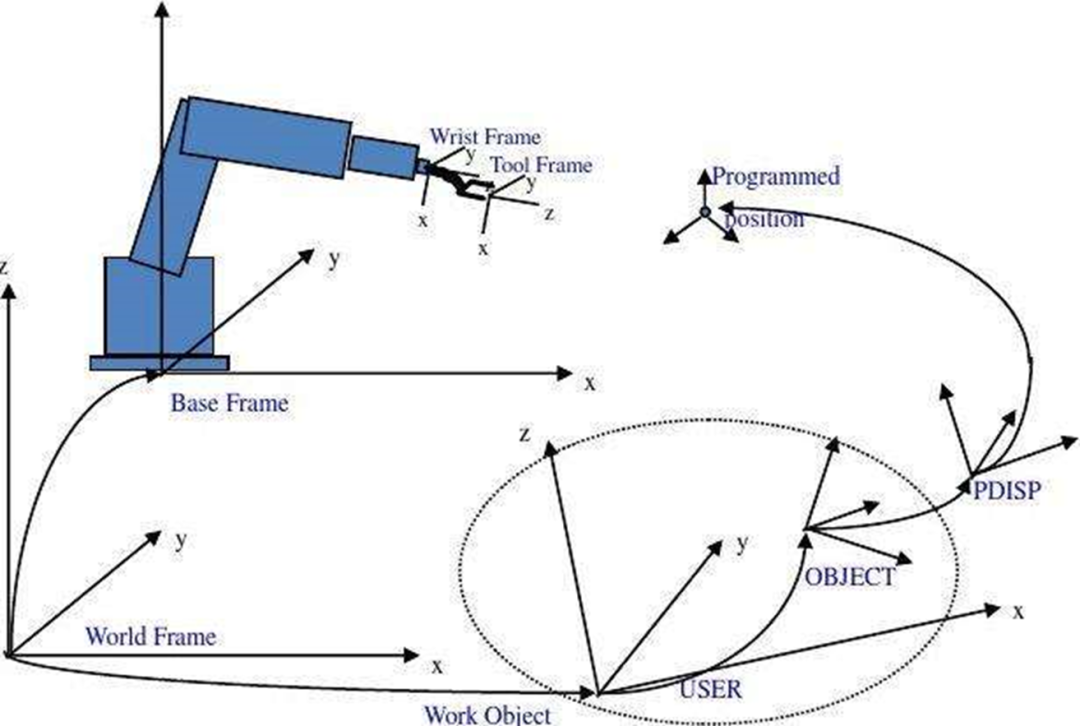
　　坐標(biāo)系

　　世界坐標(biāo)系

　　世界坐標(biāo)系的標(biāo)架　

　　相機(jī)坐標(biāo)系

　　相機(jī)默認(rèn)的位置為世界坐標(biāo)系原點(diǎn)，朝向是Z軸的負(fù)方向，正向是Y軸的正方向

　　考慮相機(jī)

　　位置就是相機(jī)的位置，也就是從哪里去觀察這個(gè)世界

　　朝向就是相機(jī)對(duì)準(zhǔn)的方向

　　正向就是相機(jī)該放在這個(gè)位置、對(duì)準(zhǔn)了方向后，該怎么擺。比如一般我們拍照，豎著擺拍出來(lái)的就是豎著的照片，橫著擺就是橫著的照片。

　　而這些參數(shù)其實(shí)也是在世界坐標(biāo)系下表示的

　　默認(rèn)的相機(jī)坐標(biāo)系

　　移動(dòng)相機(jī)之后，相機(jī)的位置、朝向、正向就改變了

　　但頂點(diǎn)的數(shù)據(jù)還是對(duì)應(yīng)著的世界坐標(biāo)系，而我們要生成圖片是依賴于相機(jī)的，所以我們要把頂點(diǎn)轉(zhuǎn)換到相機(jī)坐標(biāo)系下才行，這就是視圖的轉(zhuǎn)換。

　　視圖轉(zhuǎn)換后頂點(diǎn)的表示就是相對(duì)于相機(jī)坐標(biāo)系，但其標(biāo)架在邏輯上依然是 原點(diǎn)+三個(gè)坐標(biāo)軸

　　裁剪坐標(biāo)系

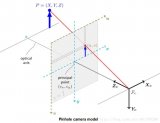
　　這還只是相機(jī)的外部參數(shù)，我們還需要確定

　　那一塊的三維區(qū)域內(nèi)的點(diǎn)，我才會(huì)拍下來(lái)，才會(huì)用來(lái)生成圖像，即我需要規(guī)定一塊“視景體”來(lái)確定拍照的范圍

　　是否需要透視效果等等其他

　　還是講坐標(biāo)變換比較實(shí)在

　　坐標(biāo)變換

　　OpenGL主要有兩個(gè)矩陣，模型視圖矩陣和投影矩陣

　　模型視圖矩陣

　　對(duì)世界坐標(biāo)系下頂點(diǎn)的變化操作，如平移、旋轉(zhuǎn)、縮放（模型）都是對(duì)頂點(diǎn)的變化，而相機(jī)的位置、朝向、正向的改變（視圖）也需要頂點(diǎn)從相對(duì)于世界坐標(biāo)系下轉(zhuǎn)換到相對(duì)于相機(jī)坐標(biāo)系，這兩種雖然是不同的改變但都是對(duì)頂點(diǎn)的操作，所以可以用一個(gè)矩陣來(lái)記錄　　

　　就是說(shuō)只要在原先點(diǎn)的基礎(chǔ)上左乘平移矩陣，就可以把點(diǎn)的坐標(biāo)進(jìn)行平移變換

　　記平移矩陣 T 為 T（dx，dy，dz），

　　旋轉(zhuǎn)

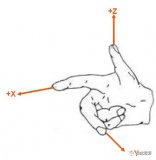
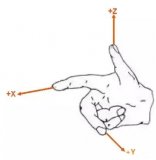
　　先考慮繞Z軸旋轉(zhuǎn)的情況，正向的旋轉(zhuǎn)為右手大拇指朝向Z軸正向時(shí)，其余手指的朝向（逆時(shí)針）

　　繞Ｚ軸旋轉(zhuǎn)至改變Ｘ和Ｙ坐標(biāo)　　

　　縮放，就是在原坐標(biāo)的基礎(chǔ)上乘以某個(gè)倍數(shù)

　　縮放矩陣

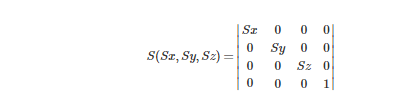
　　視圖矩陣，將以世界坐標(biāo)系原點(diǎn)為（0，0，0）點(diǎn)的世界坐標(biāo)系下的頂點(diǎn)轉(zhuǎn)換到以相機(jī)位置為（0，0，0）的相機(jī)坐標(biāo)系下。

　　頂點(diǎn)和相機(jī)之間真正相對(duì)位置是不變的，只不過(guò)我們?cè)软旤c(diǎn)的坐標(biāo)表示是在世界坐標(biāo)系下，而我們需要的是相機(jī)坐標(biāo)系下的坐標(biāo)表示。所以這里只是做坐標(biāo)變換，即同一個(gè)頂點(diǎn)在不同坐標(biāo)系下其坐標(biāo)表示是不同的。

　　從默認(rèn)的相機(jī)位置可以看到，默認(rèn)的相機(jī)坐標(biāo)系和世界坐標(biāo)系是重合的，即不需要轉(zhuǎn)換，其實(shí)也就是相當(dāng)于視圖矩陣是單位矩陣而已

　　而改變了相機(jī)的位置、朝向和正向之后，視圖矩陣才會(huì)真正的發(fā)揮作用，乘上的效果就是讓世界坐標(biāo)系下的頂點(diǎn)轉(zhuǎn)換到相機(jī)坐標(biāo)系下

　　OnenGL通過(guò)gluLookAt函數(shù)來(lái)改變相機(jī)的外部參數(shù)

　　gluLookAt（ Tx ， Ty ， Tz ， Ox ， Oy ， Oz ， Vx ， Vy ， Vz ）

　　Tx Ty Tz 為相機(jī)的位置

　　Ox Oy Oz 為相機(jī)朝向的點(diǎn)

　　Vx Vy Vz 為相機(jī)的正向

　　考慮相機(jī)的三個(gè)向量

　　n為相機(jī)朝向的方向向量

　　v為相機(jī)的正向向量

　　u為二者叉乘的向量

　　要求：n和v為互相垂直，nuv三者均為單位向量（只表方向）

　　那么可以看出這三個(gè)向量和相機(jī)坐標(biāo)系的關(guān)系

　　并且我們還知道相機(jī)的位置 Tx Ty Tz

　　對(duì)于頂點(diǎn)

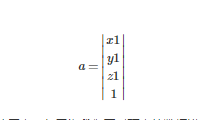
　　首先我們把相機(jī)移動(dòng)到世界坐標(biāo)系的原點(diǎn)，但因?yàn)槲覀円獙?duì)頂點(diǎn)的數(shù)據(jù)進(jìn)行修改，所以就要對(duì)頂點(diǎn)乘上 T（ -Tx ， -Ty ， -Tz ）這樣一個(gè)平移矩陣。這樣以來(lái)頂點(diǎn)移動(dòng)到了就是以相機(jī)位置為原點(diǎn)的坐標(biāo)系下

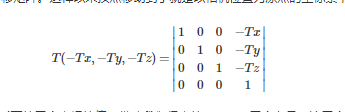
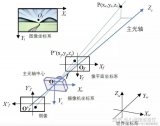
　　再求這個(gè)頂點(diǎn)在相機(jī)坐標(biāo)系下的三個(gè)坐標(biāo)的值。借助我們得出的 u，v，n三個(gè)向量，這三個(gè)向量分別對(duì)應(yīng)了相機(jī)坐標(biāo)系的三個(gè)坐標(biāo)軸，所以要求坐標(biāo)的值也就是看以這個(gè)頂點(diǎn)為終點(diǎn)、相機(jī)位置為起點(diǎn)的向量和nuv這三個(gè)單位向量的點(diǎn)積，相當(dāng)于乘上這樣一個(gè)矩陣

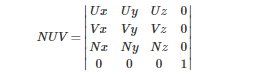
　　然后我們得到了坐標(biāo)的值嗎？還沒(méi)有。因?yàn)?向量n和坐標(biāo)軸z的正向是相反的，向量u和坐標(biāo)軸x的正向是相反的，所以我們還需要再乘上一個(gè)矩陣來(lái)調(diào)整

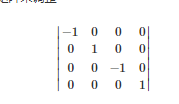
　　于是我們最終用來(lái)把世界坐標(biāo)系下的點(diǎn)轉(zhuǎn)換到相機(jī)坐標(biāo)系下的視圖矩陣就是

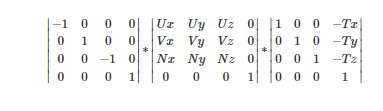
　　投影矩陣

　　模型操作對(duì)頂點(diǎn)進(jìn)行變換，其還是在世界坐標(biāo)系下

　　視圖操作將頂點(diǎn)轉(zhuǎn)換到相機(jī)坐標(biāo)系下

　　但這二者都是對(duì)頂點(diǎn)進(jìn)行變換，所以只需要一個(gè)模型-視圖矩陣來(lái)維護(hù)就可以了

　　那么投影矩陣就需要另外一個(gè)內(nèi)存空間來(lái)維護(hù)

　　因?yàn)槲覀円呀?jīng)把頂點(diǎn)轉(zhuǎn)換到了相機(jī)坐標(biāo)系下，所以我們?cè)O(shè)置視景體就以相機(jī)坐標(biāo)系來(lái)設(shè)置

　　只會(huì)glOrtho的矩陣，即正交投影。其視景體是一個(gè)方形的區(qū)域。

　　glOrtho（ left ， right ， bottom ， top ， near ， far ）

　　left，right分別對(duì)應(yīng)了x=left和x=right這兩個(gè)平面

　　bottom和top分別對(duì)應(yīng)了y=bottom和y=top這兩個(gè)平面

　　near和far分別對(duì)應(yīng)了z=-near和z=-far兩個(gè)平面

　　這里取負(fù)，主要是因?yàn)橄鄼C(jī)的朝向是z的負(fù)方向，這樣才會(huì)使視景體落在相機(jī)的前面

　　投影矩陣要做的事情，就是一個(gè)“規(guī)范化”

　　即根據(jù)視景體的范圍，對(duì)頂點(diǎn)進(jìn)行平移、放縮，使原先在視景體內(nèi)的點(diǎn)都落在以原點(diǎn)為中心、邊長(zhǎng)為2的規(guī)范化正方體內(nèi)

　　這樣做的好處就是規(guī)范，之后的裁剪、光照等等操作都在一個(gè)統(tǒng)一的規(guī)范下進(jìn)行　　

　　注意到我們放縮的時(shí)候，對(duì)于Z坐標(biāo)的放縮多了一個(gè)負(fù)號(hào)，這也就意味著所有的點(diǎn)在規(guī)范化正方體內(nèi)是Z坐標(biāo)的負(fù)號(hào)是相反的

　　這也就意味著，我們要去“看”規(guī)范化正方體內(nèi)的物體的時(shí)候，應(yīng)該從Z軸的負(fù)無(wú)窮遠(yuǎn)看向原點(diǎn)，即方向應(yīng)該是Z的正向

　　這一步得到的點(diǎn)的坐標(biāo)，我們稱其位于裁剪坐標(biāo)系