最近在做基于MIPS指令集的單周期CPU設計，其中的ALU模塊需要用到加法器，但我們知道普通的加法器是串行執行的，也就是高位的運算要依賴低位的進位，所以當輸入數據的位數較多時，會造成很大的延遲，影響整個CPU的性能，為了減小這種延遲，遂采用超前進位加法器（也叫先行進位加法器），下面來介紹一下設計的原理：

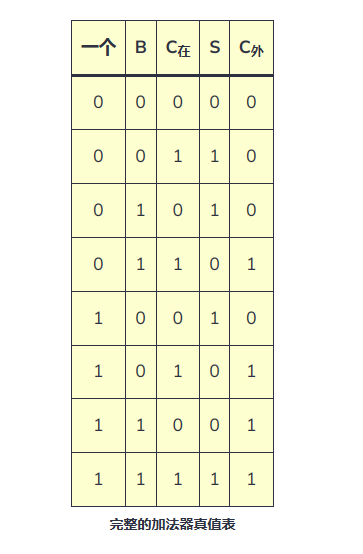
設二進制加法器第 i 位為Ai， Bi，輸出為Si，進位輸入為Ci，進位輸出為C（i+1），則有：

Si = Ai ⊕ Bi ⊕ Ci （1-1）

C(i + 1) = Ai * Bi + Ai * Ci + Bi * Ci = Ai * Bi +（Ai+Bi）* Ci （1-2）

令Gi = Ai * Bi , Pi = Ai + Bi，則: C(i + 1) = Gi + Pi * Ci

當 Ai 和 Bi 都為1時，Gi = 1， 產生進位C(i+1) = 1；

當 Ai 和 Bi 有一個為1時，Pi = 1，傳遞進位C(i+1)= Ci；

（說明：“*”表示與邏輯、“+”表示或邏輯、“⊕”表示異或邏輯）

因此Gi定義為進位產生信號，Pi定義為進位傳遞信號。Gi的優先級比Pi高，也就是說：當Gi = 1時(當然此時也有 Pi = 1)，無條件產生進位，而不管Ci是多少；當Gi = 0 而 Pi = 1時，進位輸出為Ci，跟Ci之前的邏輯有關.

第一步：設計4位超前進位加法器 (至于為什么要先設計4位的，后面有詳解)

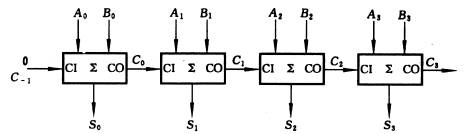
舉例：設4位加數和被加數為 A 和 B，進位輸入為C_in，進位輸出為C_out，對于第 i 位的進位產生Gi = Ai * Bi ,進位傳遞Pi = Ai + Bi , i = 0,1,2,3 。于是各級進位輸出，遞歸的展開Ci，有：

C0 = C_in

C1 = G0 + P0*C0

C2 = G1 + P1*C1 = G1 + P1*G0 + P1*P0 *C0

C3 = G2 + P2*C2 = G2 + P2*G1 + P2*P1*G0 + P2*P1*P0*C0

C4 = G3 + P3*C3 = G3 + P3*G2 + P3*P2*G1 + P3*P2*P1*G0 + P3*P2*P1*P0*C0 （1-3）

C_out = C4

由此可以看出，各級的進位彼此獨立，只與輸入數據 Ai、Bi 和 C_in有關，而且并行產生，不就達到了設計目的——將各級間的進位級聯傳播給去掉了，減小了串行進位產生的延遲。

實現上述邏輯表達式（1-3）的電路稱為超前進位部件（Carry Lookahead Unit），也稱為CLA部件。通過這種進位方式實現的加法器稱為超前進位加法器。因為各個進位是并行產生的，所以是一種并行進位加法器。

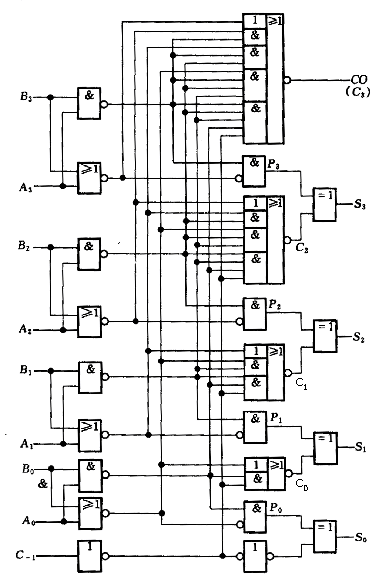
4位CLA部件電路如圖1所示：

圖1：4位CLA超前部件電路

(可能有人就想到，如果要設計32位超前進位加法器，是不是可以按照同樣的方法直接推導到C32，就可以一次性并行產生所有位的進位。。。但是，我們想想，根據表達式，進位越往后，比如C5、C6......C31、C32，表達式會越來越復雜，這是因為增加了邏輯門的輸入端個數，將會使得電路中需要具有大驅動信號和大扇入門，這會大大增加門的延遲，起不到提高電路性能的作用，這種方法叫做全先行進位，而當位數較多時，很顯然這種方式并不現實，因此更多位數的加法器可通過4位CLA部件和4位超前進位加法器來實現，后面再細說)

* 4位超前部件完成了，現在來完成4位超前進位加法器：

首先每一位都會產生進位傳遞信號和進位產生信號，然后將四位數據分別產生的進位傳遞信號和進位產生信號送到4位CLA部件，供CLA并行產生每一位的進位信號Ci，然后再送回給每一位的低進位（C_in）,就完成了4位超前進位加法器，聽不懂，沒關系，看下圖：

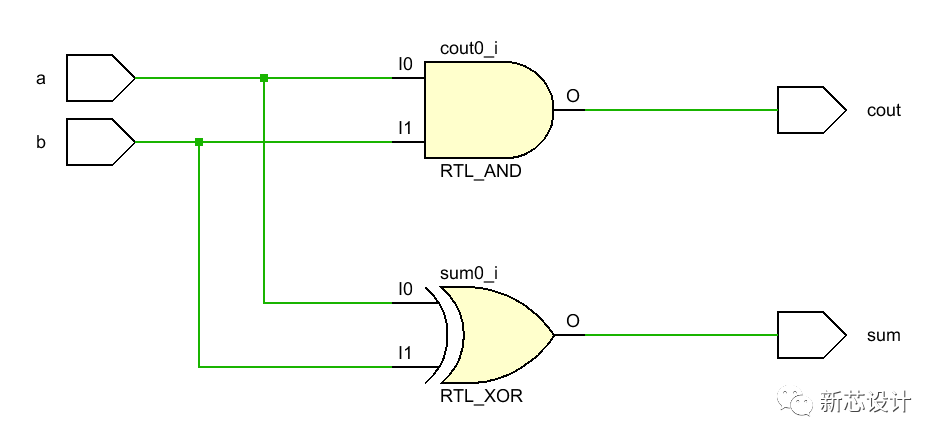
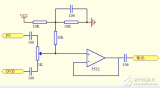
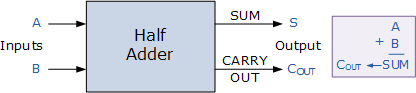
圖2：1位加法器

圖3：4位超前進位加法器

說明：1位加法器如圖2所示，輸入有A、B兩個加數，還有來自低位的進位C_in，輸出有得到的和 Si ，還有 進位產生信號Gi和進位傳遞信號Pi，之所以引出這兩個信號，是為了為后面的4位超前進位加法器做鋪墊，有人可能奇怪為什么沒有向高位的進位位，這是因為每一位的進位位是由CLA部件產生的，我們用四個如圖2所示的1位加法器和一個如圖1所示的4位超前進位部件，就組成了圖3所示的4位超前進位加法器，至此我們也就完成了4位超前進位加法器的設計。

那么，問題來了，4位超前進位加法器和我們最初要設計的32位超前進位加法器有什么聯系呢？有經驗的朋友很快就能反應過來，是不是可以用八組4位超前進位加法器級聯起來，完成32位的設計，但是，如果僅僅按照普通的級聯，也就是將八組4位超前進位加法器串聯起來，整個設計相當于組內超前進位，組間串行進位，這種方法是可行的，但不是我們的目的，因為它還是會影響整個系統的性能，為了達到最優的設計方法，我們采用組內超前進位，組間也是超前進位的方法進行設計，這種方法叫做兩級或多級先行進位加法器。

問題又來了，采用組內和組間都是超前進位的方式，到底該怎么設計呢？其實我們可以類比4位加法器的設計，為了完成4位的超前進位加法器，我們把1位加法器引出了它的進位產生信號Gi和進位傳遞信號Pi，供4位CLA使用，那么我們是否可以把4位超前進位加法器的進位產生信號Gm和進位傳遞信號Pm也引出來，然后用四組4位超前進位加法器和一個4位CLA完成16位超前進位加法器的設計呢，答案當然是可以的。

首先，我們對圖3所示的4位超前進位加法器進行封裝，并且引出進位產生信號Gm和進位傳遞信號Pm，如圖4所示：

圖4：封裝后的4位超前進位加法器

說明：圖4也是4位超前進位加法器，它和圖3的區別是引出了進位產生信號Gm和進位傳遞信號Pm，有心的朋友會發現它和圖2所示的1位加法器很相似，不同的地方僅僅是位數變成了四位，既然和1位加法器相似，那么我們就可以按照同樣的方法用四個圖4所示的4位超前進位加法器和一個CLA設計16位超前進位加法器，問題又來了，圖4所示的4位超前加法器的進位產生信號Gm和進位傳遞信號Pm怎么來的呢？

首先來看1位加法器的進位產生信號Gi和進位傳遞信號Pi是怎么來的：

既然是1位加法器，那么它的進位信號是C1，

由 C(i + 1) = Ai * Bi + Ai * Ci + Bi * Ci = Ai * Bi +（Ai+Bi）* Ci 得：

當 i = 0 時，即1位加法器的進位信號 C1 = A0 * B0 + （A0 + B0）* C0

我們把 （A0 * B0）叫做進位產生信號Gi，把（A0 + B0）叫做進位傳遞信號Pi 【原因前面已經講過】

顯然 Gi 和 Pi 分別時1位加法器的進位產生信號和進位傳遞信號.

再來看4位加法器的進位產生信號Gm和進位傳遞信號Pm該怎么來：

既然是4位加法器，那么它的進位信號是C4，

由 C(i + 1) = Ai * Bi + Ai * Ci + Bi * Ci = Ai * Bi +（Ai+Bi）* Ci 得：

當 i = 3 時，即4位加法器的進位信號

C4 = A3 * B3 + （A3 + B3）* C3

= G3 + P3*C3

= G3 + P3*G2 + P3*P2*G1 + P3*P2*P1*G0 +P3*P2*P1*P0*C0【在設計4位CLA時已經給出】

類比法得：把（G3 + P3*G2 + P3*P2*G1 + P3*P2*P1*G0）叫做進位產生信號Gm，（P3*P2*P1*P0） 叫做進位傳遞信號Pm，顯然 Gm 和 Pm 分別是四位加法器的進位產生信號和進位傳遞信號.

第二步：設計16位超前進位加法器

首先每一個封裝后的4位超前進位加法器都會都會輸出進位產生信號和進位傳遞信號，將四個4位超前進位加法器輸出的進位產生信號和進位傳遞信號輸入到4位CLA中，供CLA產生每一個4位超前進位加法的低進位信號，如下圖所示：

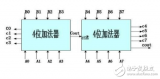
圖5：16位超前進位加法器

至此，我們完成了16位超前進位加法器的設計。

要想設計32位超前進位加法器和設計16位超前進位加法器一樣的方法，對16位超前進位加法器進行封裝，引出16位加法器的進位產生信號Gx和進位傳遞信號Px即可。

第三步：設計32位超前進位加法器

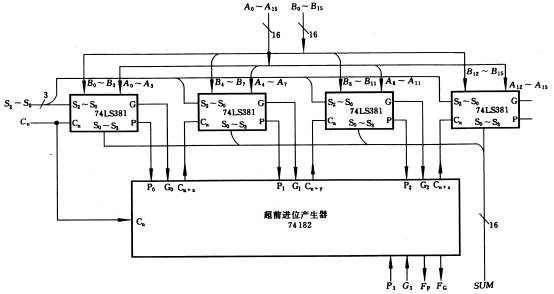
因為我們已經有了16位超前進位加法器，并且已經引出了進位產生信號Gx和進位傳遞信號Px，那么我們只需要兩個16位的超前進位加法器即可組成32位的加法器，但是超前部件CLA是4位的，意味著我們只需要用到CLA的低兩位，所以整個32位的超前進位加法器模塊圖如下所示：

圖6：32位超前進位加法器

至此，32位超前進位加法器完成。

回顧：此次32位超前進位加法器的設計以4位超前進位加法器和4位CLA部件為基礎，采用組內和組間都是超前進位的方式，有效的減小了傳統加法器串行進位導致的延遲問題，采用這種方法，只要設計合適位數的CLA部件，就可以設計任意位數的超前進位加法器，需要注意的地方就是進位產生信號和進位傳遞信號的理解，以及CLA部件的理解，下面附上此次設計的源碼以及仿真波形圖：

1位加法器：

4位CLA部件：

4位超前進位加法器：

4位超前進位加法器RTL視圖：

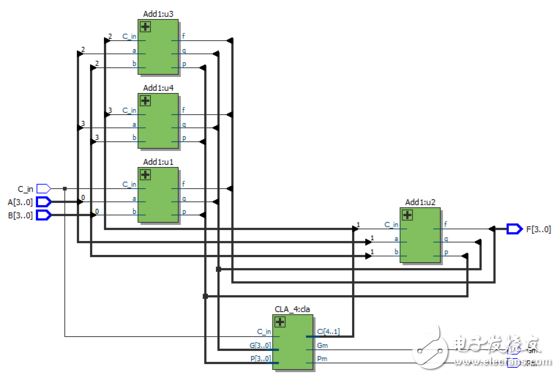
16位超前進位加法器：

16位超前進位加法器RTL視圖：

32位超前進位加法器：

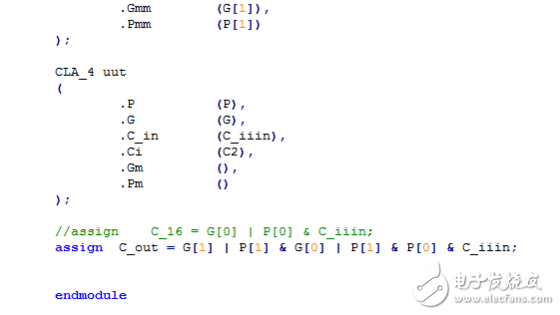
32位超前進位加法器RTL視圖：

但是，我們發現如果在32位超前進位加法器中調用整個4位CLA，而我們僅僅只使用了兩位，導致了資源的浪費，所以，我們修改代碼如下：

*32位超前進位加法器：

*32位超前進位加法器RTL視圖：

*32位超前進位加法器仿真激勵：

*32位超前進位加法器仿真波形圖：

從波形圖上可以看出，32位超前進位加法器功能正確，只要理解了設計的目的，以及設計的思想，實現這個加法器并不困難，所以理解很重要，希望能給正在學習計算機原理與組成的朋友幫上忙，謝謝！

如有不足的地方，還請指正！