用C 語言描述AES256 加密算法，然后在硬件中加速性能。

高級加密標準 (AES) 已經成為很多應用（諸如嵌入式系統中的應用等）中日漸流行的密碼規范。自從 2002 年美國國家標準技術研究所 (NIST) 將此規范選為標準規范以來，處理器、微控制器、FPGA和 SoC 應用的開發人員就開始利用 AES 來保護輸入、輸出及保存在系統中的數據。我們可在更高抽象層上非常高效地描述算法，就像用于傳統軟件開發中那樣；但由于涉及到的操作，該算法在 FPGA中實現起來最為高效。開發人員甚至可在布線中“免費”獲得一些操作。

基于這些原因，AES 是個絕佳的例子，即開發人員可利用 C 語言描述算法，然后在硬件中加速實現，從而受益于賽靈思 SDSoC ? 開發環境。本文中我們就是要這樣做，首先熟悉一下 AES 算法，然后在賽靈思 Zynq?-7000 All Programmable SoC 的處理系統 (PS) 上實現 AES256（256 位秘鑰長度）以建立軟件性能基準，然后再在片上可編程邏輯 (PL)中進行加速。為了完全了解可獲得的優勢，我們將在 SDSoC 環境所支持的全部三個操作系統中執行這幾個步驟，三個操作系統為：Linux、FreeRTOS 和裸機。

算法
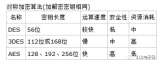
AES 屬于對稱塊密碼，可采用 128、192 和 256位不同的秘鑰長度。秘鑰長度決定加密或解密數據所需的處理步驟數。顧名思義，塊密碼算法采用的是數據塊。AES 算法一次處理 16 字節的固定模塊。因此，如果我們密碼內容少于 16 字節，就必須將未使用的字節進行填充。

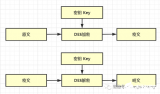
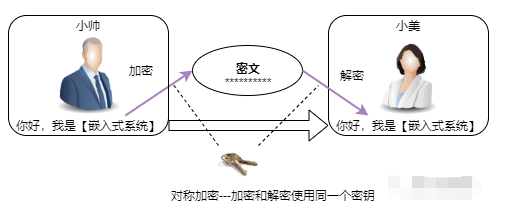
由于 AES 是對稱密碼，信息加密和解密都采用相同的做法和秘鑰。相反，非對稱算法（例如RSA）則使用不同秘鑰進行數據加密和解密。

AES 算法中四個階段中每個階段都代表一個狀態。四個 AES 階段的組合稱為一個循環。所需循環的數量取決于秘鑰長度。

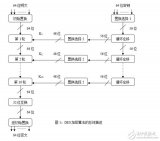
很簡單，AES 狀態起始于我們要加密的 16 個字節。每個新步驟都會對狀態進行更新。處理狀態之前，我們需要將輸入字節串變為初始狀態，即 4 x 4矩陣（圖 1）。

圖 1 — 16 字節的初始狀態轉換為 4 x 4 矩陣

現在，我們將最初的 16 個字節重新編排為 4 x4 矩陣形式的初始狀態，便可研究每個步驟如何操縱它的輸入狀態。

輪密鑰加(AddRoundKey) ： 這是唯一使用加密秘鑰的步驟。我們已經注意到，所需的加密算法循環的數量取決于秘鑰長度（128、192 或 256 位）。必須對加密秘鑰進行秘鑰擴展，以確保在每個循環中不會重新使用秘鑰中的字節。果然，對于不同的秘鑰長度而言擴展秘鑰長度并不相同。擴展秘鑰長度為：
擴展秘鑰長度（字節）= 16 *（循環 + 1）

這個步驟中的操作很簡單。輸入狀態字節與擴展秘鑰的 16 個字節進行異或運算。每個循環使用擴展秘鑰的不同部分；循環 0 使用字節 0 至 15，循環1 使用字節 16 至 31，以此類推。對于每個循環，狀態的字節 1 與擴展秘鑰的最低有效字節進行異或運算，字節 2 與“最低有效字節+1”進行異或運算，以此類推。

字節替換 (SubBytes) ： 該步驟利用字節替換將狀態值用另一個值替換出去。替換盒中的值是預先設定的，而且輸入位于輸出位之間的關聯較小。替換盒 (S-box) 是一個 16 x 16 矩陣。我們使用被替代字節的高四位和低四位作為替代表格中的索引。例如，使用圖 2 中的 S-box 加密，如果第一個初始狀態字節為 0 x 69，那么用替代值 0 x F9 代替。狀態字節的高四位選擇替代表格的行； 低四位選擇列。注意在圖 2 中，加密和解密使用不同的替換盒，而且盒中內容不同。

圖 2 — AES S-box 內容

行位移變換 (ShiftRows) ：該步驟對每行執行循環字節移位，以重新排列輸入狀態矩陣。 我們將每行右旋不同個因數（圖 3）。第 1 行不變。將第 2 行移動 1 個字節，第 3 行移動 2 個字節，第 4 行移動3 個字節。解密時執行相同操作，但向左旋轉而非向右。

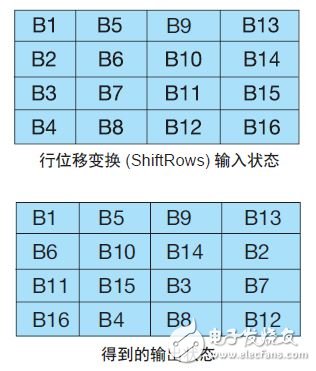
圖 3 — 行位移變換 (ShiftRows) 操作

列混合變換 (MixColumns) ：這是循環中最復雜的步驟，需要進行 16 次乘法和 12 次異或運算。逐列對輸入狀態矩陣進行此操作，將輸入狀態矩陣與固定矩陣相乘以獲得新的狀態列（圖 4）。列中的每項與矩陣中的一行相乘。將每次乘法結果進行異或運算，以獲得新的狀態值。第一個要進行相乘運算的列和行在圖 4 中加亮顯示。

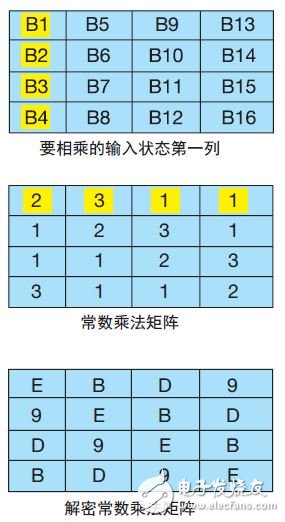
圖 4 — 用于加密和解密的列混合變換 (MixColumns) 函數

以下是第一列的列混合變換(MixColumns) 方程：
B1’ = (B1 * 2) XOR (B2 * 3) XOR (B3 * 1) XOR (B4 * 1)
B2’ = (B1 * 1) XOR (B2 * 2) XOR (B3 * 3) XOR (B4 * 1)
B3’ = (B1 * 1) XOR (B2 * 1) XOR (B3 * 2) XOR (B4 * 3)
B4’ = (B1 * 3) XOR (B2 * 1) XOR (B3 * 1) XOR (B4 * 2)

然后，為輸入狀態中的下一個列采用相同乘法矩陣重復這個過程，直到處理完所有輸入狀態列。

既然我們已經理解了 AES 加密和解密算法所需的詳細步驟，那么還需要知道一個循環中這些步驟的應用順序以及我們是否必須為每個循環應用所有步驟。每個 AES 加密循環都包含全部四個步驟，并按照以下順序：
1. 字節替換 (SubBytes) ;
2. 行位移變換 (ShiftRows);
3. 列混合變換 (MixColumns) （只針對循環 1 至N–1）;
4. 輪密鑰加 (AddRoundKey)（ 使用擴展秘鑰）。

當然，我們需要能夠反轉這個過程，將不可讀的密文變回純文本，讓加密信息有用。為此，我們將步驟進行如下排序：
1. 反轉行位移變換；
2. 反轉字節替換；
3. 輪密鑰加（使用擴展秘鑰）;
4. 反轉列混合變換（只針對循環 1 至 N–1）。
執行第一輪加密之前，我們需要為加密和解密執行初始輪密鑰加 (AddRoundKey) 操作。

可在更高抽象層上高效地描述 AES，就像在傳統軟件開發中那樣，但在 FPGA 中實現起來最為高效。開發人員甚至可在布線中“免費”獲得一些操作。

我們看一下擴展秘鑰必須使用的算法，以便提供足夠的秘鑰位，用以執行相應數量的輪密鑰加(AddRoundKey) 步驟（圖 5）。進行秘鑰擴展時，16、24 或 32 字節的秘鑰長度分別需要 44、52 或 60個循環。擴展秘鑰的第一個字節等于初始秘鑰。這意味著對于我們的 AES256 實例來說，擴展秘鑰的最開始的 32 個字節就是秘鑰本身。秘鑰擴展操作在每次迭代中為擴展秘鑰生成 32 個附加位。

圖 5 — 秘鑰擴展算法

擴展秘鑰的第一個字節等于初始秘鑰。這意味著對于我們的 AES256 實例來說，擴展秘鑰的最開始的 32 個字節就是秘鑰本身。

以下是重要的擴展步驟：
RotateWord: 與行位移變換 (ShiftRows) 類似，這個步驟重新組織 32 位字，以使最高有效字節變為最低有效字節。
SubWord: 這個步驟使用的替換盒與加密時進行字節替換所使用的替換盒相同。
rcon: 該階段對用戶定義的值進行 2 次冪運算。
與列混合變換 (MixColumns) 階段類似，rcon 也在有限域 (28) 中執行； 因此這個步驟普遍使用預先計算的查找表。
EK: 從擴展秘鑰返回 4 個字節。
K: 與 EK 類似，從秘鑰返回 4 個字節。
如何知道我們已經正確實現了加密和秘鑰擴展算法？ AES 的 NIST 規范包含多個有效實例，可用來檢查我們自己的實現結果。

創建代碼
為了確保能夠加速 Zynq SoC 的 PL 中 AES 代碼的加密部分，我們必須一開始就要以這個目標來開發代碼（見這里的編碼規則）。要考慮的第一件事是算法的架構；我們需要正確對其進行分段。AES 很適合這種方案，因為我們可以為每個階段編寫函數，然后再根據需要調用。 我們還必須編寫要在自身的文件中進行加速的函數。軟件架構包括以下內容。

main.c: 該文件包含秘鑰擴展算法、加密秘鑰和純文本輸入，以及對 AES 加密函數的調用。

aes_enc.c: 該文件執行加密。我們將每個階段編寫為單獨的函數，這樣就能根據 AES 循環的需要進行調用。為確保程序設計對于處理器上執行的程序具有通用性，我們為混合步驟的乘法使用查找表。

aes_enc.h: 這個文件包含 aes_function 的定義以及用來確定大小的參數（例如 mk、nb 和 nr）。

sbox.h: 這個文件包含用于替換字節的替換盒、執行秘鑰擴展的 rcon 函數的查找表以及用于列混合變換乘法的乘法查找表。

在這個結構中，我們可以選擇 AES 加密函數( 圖 6) 作為要進行加速的函數，只需右鍵點擊該函數并選擇“ Toggle HW/SW”即可。

圖 6 — 要加速的函數

為了能確定基準性能以及通過函數加速獲得的保存結果，我們必須對函數的執行進行時間控制。為此，我們使用 sds_lib.h 中的sds_clock_counter。

編寫源代碼（在 github 提供）之后，在用 ZynqSoC 中的單個 ARM? Cortex ? -A9 處理器內核在軟件中執行 AES 算法時，我記錄了 36,662 個處理器周期。

為加速而進行的優化
加速 AES 算法比前一個問題中的矩陣乘法算法還要稍稍復雜一些。這是因為 AES 算法的主循環包含互相依賴的階段。

我加速 AES 算法時所采用的方法是：檢查循環以找出可以展開的地方； 優化存儲器帶寬； 選擇正確的數據移動時鐘頻率和硬件功能頻率。

AES 加密函數的主循環包含用于執行每個 AES步驟的函數。AES 算法中的每個函數必須完整執行，并在下個函數運行之前計算出結果。這種互相依賴性需要我們將精力集中于作為獨立函數的 AES步驟。這些步驟中存在足夠多的優化潛力。

我們可將輪密鑰加 (AddRoundKey) 、字節替換(SubBytes) 和列混合變換 (MixColumns) 步驟流水線化，以提高性能。在這些函數中，我們通過將編譯指示放在第一個循環中來執行 HLS Pipeline 命令。我們應展開內部循環。這些函數中有幾個函數從查找表（通常從 block RAM 構建）讀取數據。我們需要增加存儲器帶寬，在本例中，我將編譯指示參數指定為“完成”，這樣可將存儲器內容實現為分立寄存器而非BRAM。

在 Zynq SoC 上的 PS 與 PL 之間傳輸數據的能力對提升性能而言也非常重要。我所做的第一步是將數據移動時鐘網絡設定為最高時鐘頻率：200MHz。第二個方案是確保為 PS 與 PL 之間的數據傳輸使用直接存儲器訪問。為此，我必須將接口稍加修改，并使用 sds_alloc 函數按照 DMA 傳輸的要求確保數據在存儲器中的連續性（圖 7）。

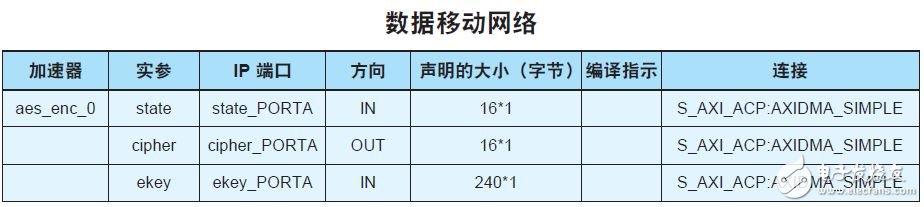
圖 7 — PS 與 PL 之間的數據移動網絡

第二個也是最后的優化步驟是將硬件功能的時鐘速率設定在所支持的最高頻率：166.67 MHz。

操作系統支持
當我最終將所有內容放在一起并構建出這個實例時，經 PL 加速的 AES 代碼在 Linux 上運行16,544 個處理器時鐘周期； 當在單獨在軟件中運行
AES 代碼時，只需要 45%(16,544/36,662) 的周期數量。這可將這個具有互相依賴關系且相當復雜的算法的執行時間縮短 55%。

當然，我們也可在 SDSoC 環境中選擇 BareMetal或 FreeRTOS 操作系統。創建 BareMetal 和 FreeRTOS項目并重新使用代碼能夠在三種操作系統之間進行性能對比。對于給定項目而言，操作系統的選擇取決于任務要求、性能預算以及響應時間。

圖 8 給出了 Zynq SoC 的 PS 和 PL 中三種操作系統的性能( 圖 8)。

圖 8 — Zynq PS 和 PL 中的操作系統性能。FreeRTOS 和 BareMetal 提供類似的縮短效果。

不出意料，FreeRTOS 和 BareMetal 實現了類似的時間縮短效果，因為兩種操作系統都比完整的 LinuxOS 簡單得多。

正如我們的結果所示，利用 SDSoC 開發環境加速 AES 加密，能實現真正的性能提升，而且易于實現—— 無需深入的 FPGA 設計經驗。