正文部分

電機鐵心是電機內的關鍵部件，其性能的改善對電機整體性能的提升具有重要意義。永磁電機本身性能較為優異，同時與一般的電機設計相比，再制造電機還受到原有鐵心結構的限制，因此其性能難以提升。傳統電機鐵心材料一般選用冷軋硅鋼片，而非晶合金材料與硅鋼片相比，其加工過程更加環保，且具有更低的鐵心損耗，應用于電機鐵心可以使電機鐵耗顯著降低，從而提高效率。

1 電機參數及混合疊壓方法

1.1 定子材料

原電機所用的硅鋼材料牌號為B35AV1900，所用非晶合金材料牌號為Metglas2605SA1。圖1為由湖南聯眾MATS-2010S軟磁測量裝置測得的硅鋼材料和非晶合金試樣的磁化曲線。對比兩者磁化曲線可知，硅鋼材料的飽和磁通密度（簡稱“磁密”）約為1.80 T，非晶合金的飽和磁通密度約為1.44 T，在相同磁場強度情況下，非晶合金對應的磁通密度小于硅鋼材料的磁通密度。

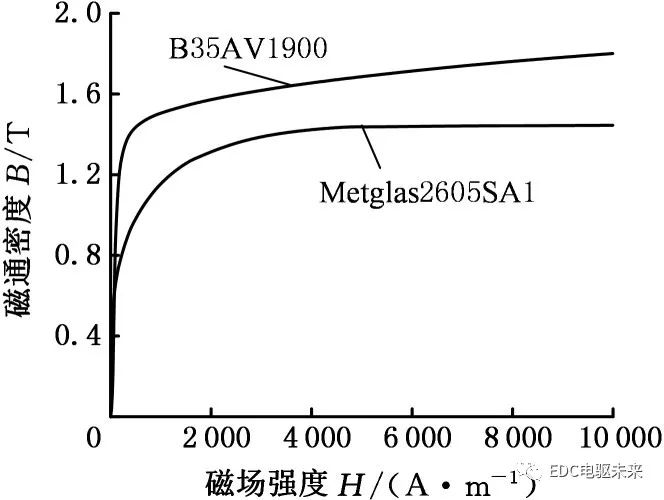
圖1 硅鋼和非晶合金的磁化曲線
Fig.1 Magnetization curves of silicon steel and amorphous alloy

1.2 電機參數

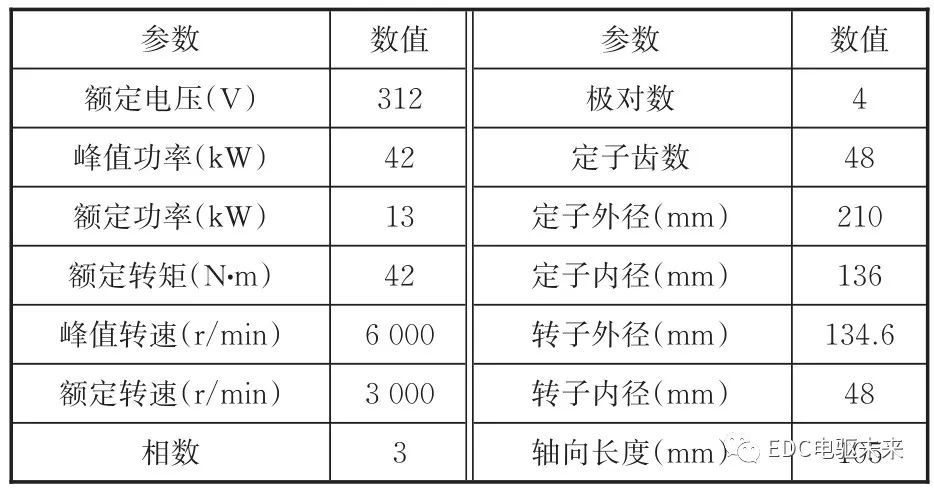
以一臺8極48槽內置式永磁同步電機為例進行定子混合疊壓再制造。電機的參數見表1。

表1 電機主要參數
Tab.1 Main parameters of motor

1.3 混合疊壓方法

受到原鐵心材料和結構的限制，再制造的電機鐵心性能較差。利用性能優異的非晶材料替換原鐵心，可以顯著降低鐵心的損耗，但非晶材料飽和磁密較小，且成本較高。通過合理選擇材料比例，將非晶材料與硅鋼材料組合使用，既能降低電機損耗、提升電機綜合性能，又能充分利用零部件，降低再制造成本。定子混合疊壓是將不同材料沿電機軸向間隔疊壓制成定子鐵心，規定相同材料的每段疊片段長度相等。再制造時，不同疊片段除材料不同外，鐵心結構與尺寸均相同，并保持與原電機一致。混合疊壓定子見圖2，其中A和B代表不同的材料。

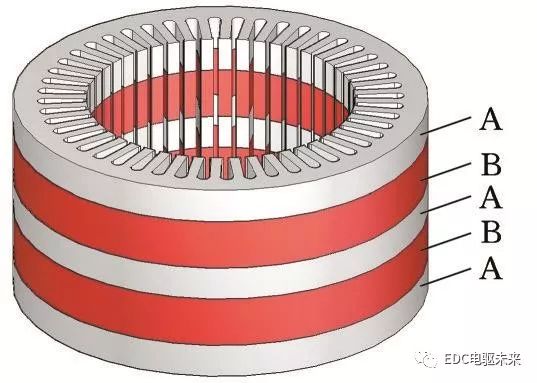
圖2 混合疊壓定子鐵心
Fig.2 Hybrid laminated stator core

2 混合疊壓電機的齒槽轉矩分析

由文獻［13］可知，對于使用同種材料的永磁同步電機，根據能量法，齒槽轉矩可以定義為空載時電機內部磁場能量與定轉子相對位置角的負導數，即

式中，Tcog為齒槽轉矩；W為磁場能量；α為定轉子相對位置角。

在混合疊壓電機中，定子由不同的材料組合而成，材料本身的磁導率不同，對電機內部與氣隙中磁場的分布具有一定影響；同時非晶材料飽和磁密較小，對材料交界面區域處的磁場分布具有一定的影響，但通常而言，其影響范圍與程度不會很大。考慮到定子混合疊壓電機的特征，若不計材料間的相互影響，可通過各材料段對應區域能量的疊加得到電機內部的總能量，進一步便可得到定子混合疊壓電機的齒槽轉矩：

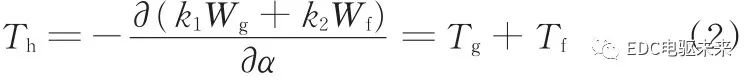
式中，Th為混合電機的齒槽轉矩；Wg為硅鋼段區域對應的磁場能量；Wf為非晶段區域對應的磁場能量；k1、k2分別為硅鋼和非晶的分段數；Tg為硅鋼疊片段的齒槽轉矩之和；Tf為非晶疊片段的齒槽轉矩之和。

由式（2）可知，在忽略材料間相互影響的情況下，混合疊壓電機的齒槽轉矩可以由對應材料各自齒槽轉矩的疊加得到。若引入材料混合比，并以電機軸向長度為基準，則混合電機齒槽轉矩近似計算為

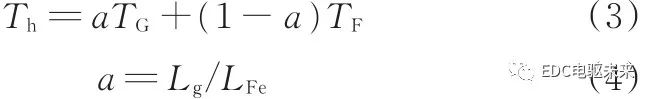
式中，TG、TF分別為純硅鋼定子電機和純非晶定子電機的齒槽轉矩；a為硅鋼材料所占的比例；Lg為硅鋼材料所有疊片分段的軸向長度之和；LFe為定子軸向長度。

由式（2）和式（3）可知，利用對應材料的二維有限元計算結果近似疊加可得到混合電機的齒槽轉矩，可避免復雜的解析推導和三維分析，這為混合電機齒槽轉矩的優化設計和研究提供了便利。

3 再制造電機齒槽轉矩分析

3.1 混合疊壓電機模型的建立

考慮到三維仿真時間長，占用資源多，本文利用Ansoft內部計算軟件Rmxprt生成原電機1/8模型。在此基礎上將定子鐵心刪除，替換為混合疊壓定子鐵心，即得到定子混合疊壓再制造電機的仿真模型。

齒槽轉矩的仿真對網格要求較高，因此將繞組刪除，減少網格數量，采用氣隙分層的方法加密網格，同時電機轉速設置成低轉速，以保證分析結果的準確性。剖分結果見圖3。

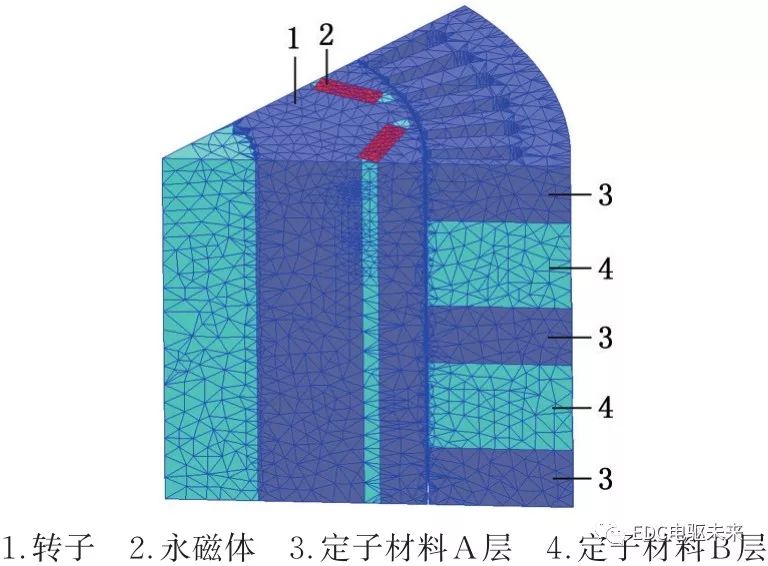
圖3 電機網格剖分
Fig.3 Mesh generation of motor

3.2 材料對齒槽轉矩的影響

定子混合疊壓再制造電機的定子由兩種材料混合疊壓制成。兩種材料的磁性能不同，在研究不同材料的混合比例和疊壓方式對齒槽轉矩的影響規律之前，有必要對不同材料本身對電機齒槽轉矩的影響規律進行研究。再制造電機所用材料為非晶材料和硅鋼材料，對圖3所示模型中定子的所有分層同時賦予硅鋼或非晶材料，得到兩種材料的齒槽轉矩波形圖，見圖4。

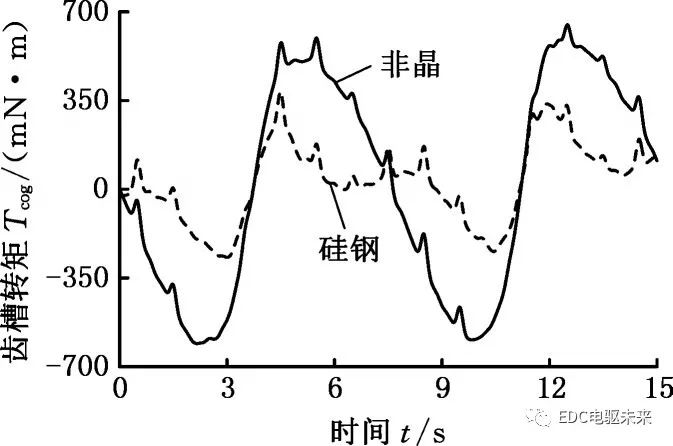
圖4 不同材料的齒槽轉矩
Fig.4 Cogging torque of different materials

由圖4可以看出，兩種材料齒槽轉矩波形不同，幅值相差較大。對其波形進行傅里葉分解，得到諧波幅值圖，見圖5。

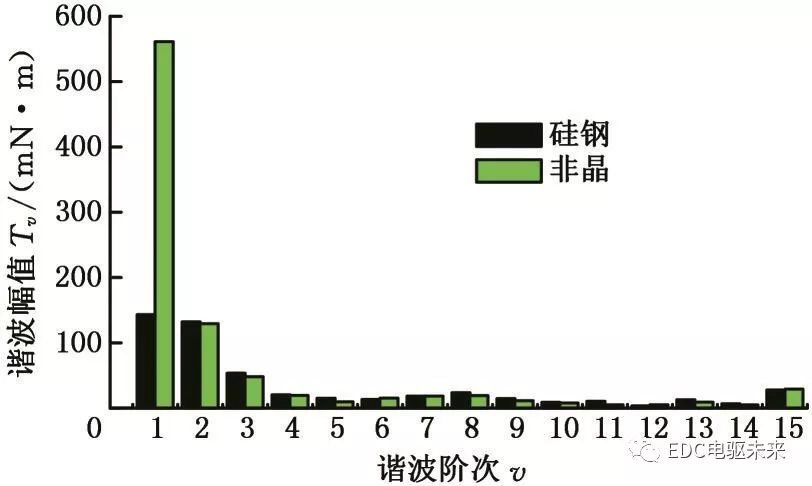
圖5 不同材料齒槽轉矩的諧波分析
Fig.5 Harmonic analysis of the cogging torque of different materials

對比各次諧波的大小可知，非晶電機基波幅值為561 mN·m，硅鋼電機基波幅值為143 mN·m，非晶電機基波幅值大約是硅鋼電機的4倍；其他各次諧波幅值大小基本相同，最大差值為10 mN·m。結果表明，對替換定子而言，硅鋼與非晶兩種材料磁性能的差異對齒槽轉矩的影響主要體現在基波幅值上，對其他各次諧波的影響較小。對于定子由這兩種材料混合疊壓而成的電機，兩種材料混合使用引入的相互間的影響情況以及不同疊壓方式帶來的附加影響情況還有待研究。

3.3 疊壓方式對齒槽轉矩的影響

以50%比例混合為例（硅鋼與非晶材料以1∶1的比例混合疊壓制成再制造電機定子鐵心）研究不同疊壓方式對混合電機齒槽轉矩的影響規律。對圖3所示定子中3、4對應的分段分別以硅鋼-非晶和非晶-硅鋼的順序賦予材料，得到兩種混合疊壓定子；其疊壓順序不同，對應材料的分段數也不同。用這兩種定子替換原電機定子，進行有限元仿真，得到兩種疊壓方式下電機的齒槽轉矩，見圖6。

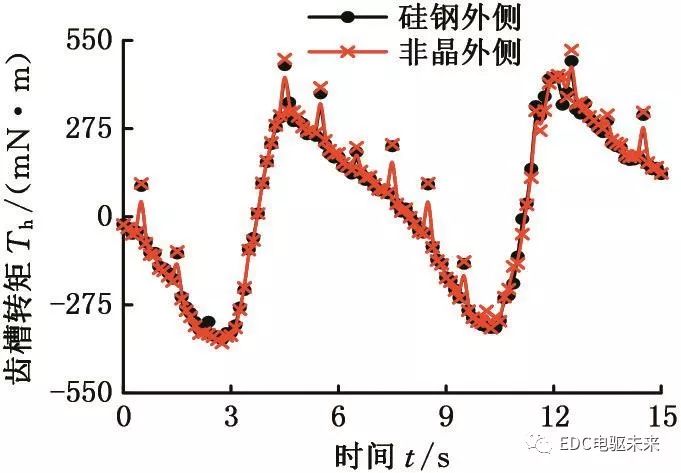
圖6 不同疊壓方式的齒槽轉矩
Fig.6 Cogging torque with different stacking modes

從圖6中可以看出，不同疊壓方式下電機的齒槽轉矩波形基本一致。對這兩種疊壓方式下電機齒槽轉矩波形進行傅里葉分解，得到兩者各次諧波幅值，見圖7，可以看出，不同疊壓方式下，電機的基波與各次諧波幅值相差較小，最大差值為11 mN·m。分析結果表明，隨著材料分段數和疊壓順序的變化，電機齒槽轉矩沒有明顯的變化。可以認為在空載的情況下，當混合比例與總的分段數一定時，各材料的分段數和疊壓順序不會改變電機內部磁場能量的變化規律，因此對齒槽轉矩的影響較小。

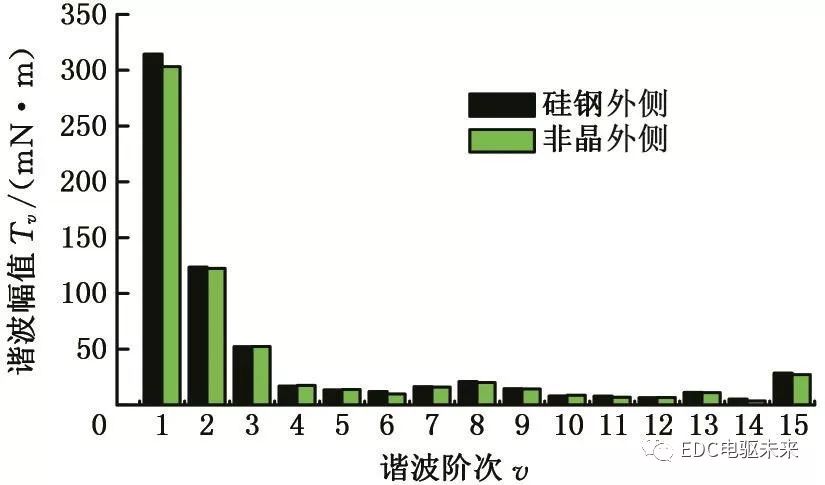
圖7 不同疊壓方式的齒槽轉矩諧波分析
Fig.7 Harmonic analysis of cogging torque with different stacking modes

3.4 齒槽轉矩的分段疊加

由于電機鐵心內部磁場分布較為復雜，混合電機的磁場分布規律尚不明確，故解析計算較為困難。現以硅鋼與非晶材料以1∶1、1∶5、5∶1比例進行混合疊壓為例進行研究。通過二維仿真得到定子由純硅鋼材料和純非晶材料組成的電機的齒槽轉矩，并根據式（3）按照相應的材料混合比例進行疊加近似計算。疊加結果與三維整體仿真所得齒槽轉矩進行對比。結果如圖8～圖10所示。

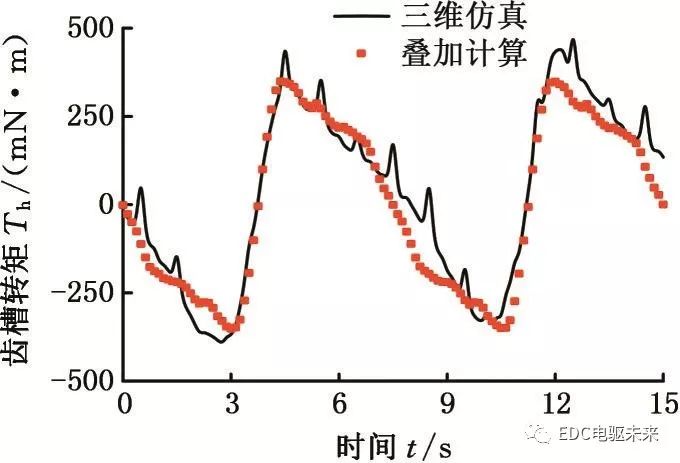
圖8 硅鋼非晶1∶1混合時的齒槽轉矩
Fig.8 Cogging torque of silicon steel and amorphous material when mixed with 1∶1 ratio

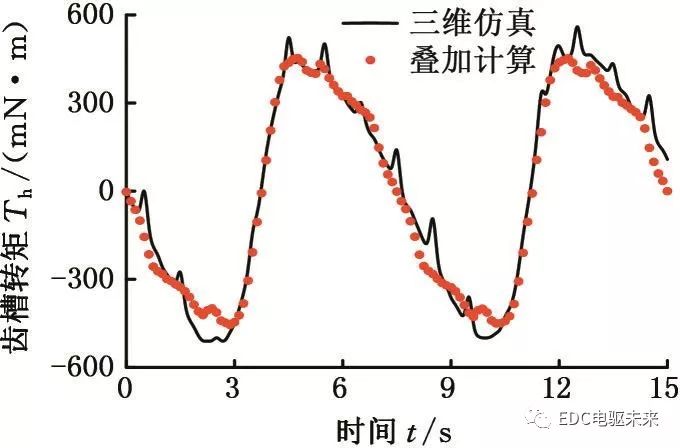
圖9 硅鋼非晶1∶5混合時的齒槽轉矩
Fig.9 Cogging torque of silicon steel and amorphous material when mixed with 1∶5 ratio

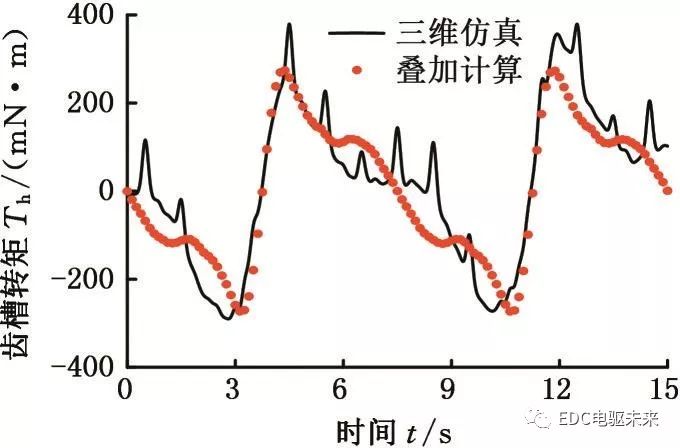
圖10 硅鋼非晶5∶1混合時的齒槽轉矩
Fig.10 Cogging torque of silicon steel and amorphous material when mixed with 5∶1 ratio

分別對比兩者齒槽轉矩波形可知：由于二維計算無法考慮端部效應以及材料之間的相互影響，故疊加所得齒槽轉矩與三維仿真結果存在一定的差異；不同比例下疊加計算所得齒槽轉矩幅值與三維仿真所得齒槽轉矩幅值相差不大，且波形基本一致。對比分析驗證了分段疊加近似計算混合疊壓電機齒槽轉矩的有效性，節約了時間和資源，為齒槽轉矩的優化分析提供便利。

4 混合比例的選取與齒槽轉矩的優化

由非晶合金與硅鋼材料的磁化曲線可知：一方面，同一外磁場作用下，非晶合金的磁密較小，應用于定子鐵心，能顯著降低電機的鐵心損耗，但非晶材料的飽和磁密較小，在同樣磁場激勵下，非晶材料更容易飽和，導致其磁導率下降，對氣隙磁密和電機各項性能造成一定影響；另一方面，通過不同比例下齒槽轉矩的對比可知，混合疊壓之后得到的電機齒槽轉矩大于原硅鋼電機的齒槽轉矩，且會隨著非晶材料比例的增大而增大；此外，由于非晶合金本身脆硬的特性，其加工較為困難，成本也相對較高。結合文獻［8］給出的再制造成本特征，混合疊壓時，應綜合考慮再制造成本與電機性能，選取合適的材料比例。

4.1 不同比例下電機性能分析

不同比例下混合疊壓電機與原硅鋼電機各項性能參數見表2。

對比不同混合比例下電機與原電機的各項參數可知：空載時混合疊壓電機與原硅鋼電機相比，磁鏈與電動勢基本不變，電動勢的諧波畸變率變小，氣隙磁密幅值略有降低，且非晶段的氣隙磁密幅值明顯低于硅鋼段的氣隙磁密幅值，同時隨著非晶材料比例的增多，齒槽轉矩逐漸增大；額定工況下，由于非晶材料優越的低損耗特性，電機損耗明顯下降，電機效率略有提升，但由于非晶材料的飽和磁密較小，因此輸出轉矩略有收縮，且收縮率隨著非晶材料比例的增大而增大。

由對比分析結果可知，混合疊壓電機相比于原電機，空載性能基本不變，電機損耗明顯降低，但也存在齒槽轉矩增大，輸出轉矩減小的問題。為綜合考慮混合疊壓電機損耗降低與轉矩收縮的影響，選擇合適的材料比例，現以定子材料為純非晶合金作為基準，將不同混合比例下電機效率的提升值進行換算，換算公式為

表2 電機性能參數對比
Tab.2 Comparison of motor performance parameter

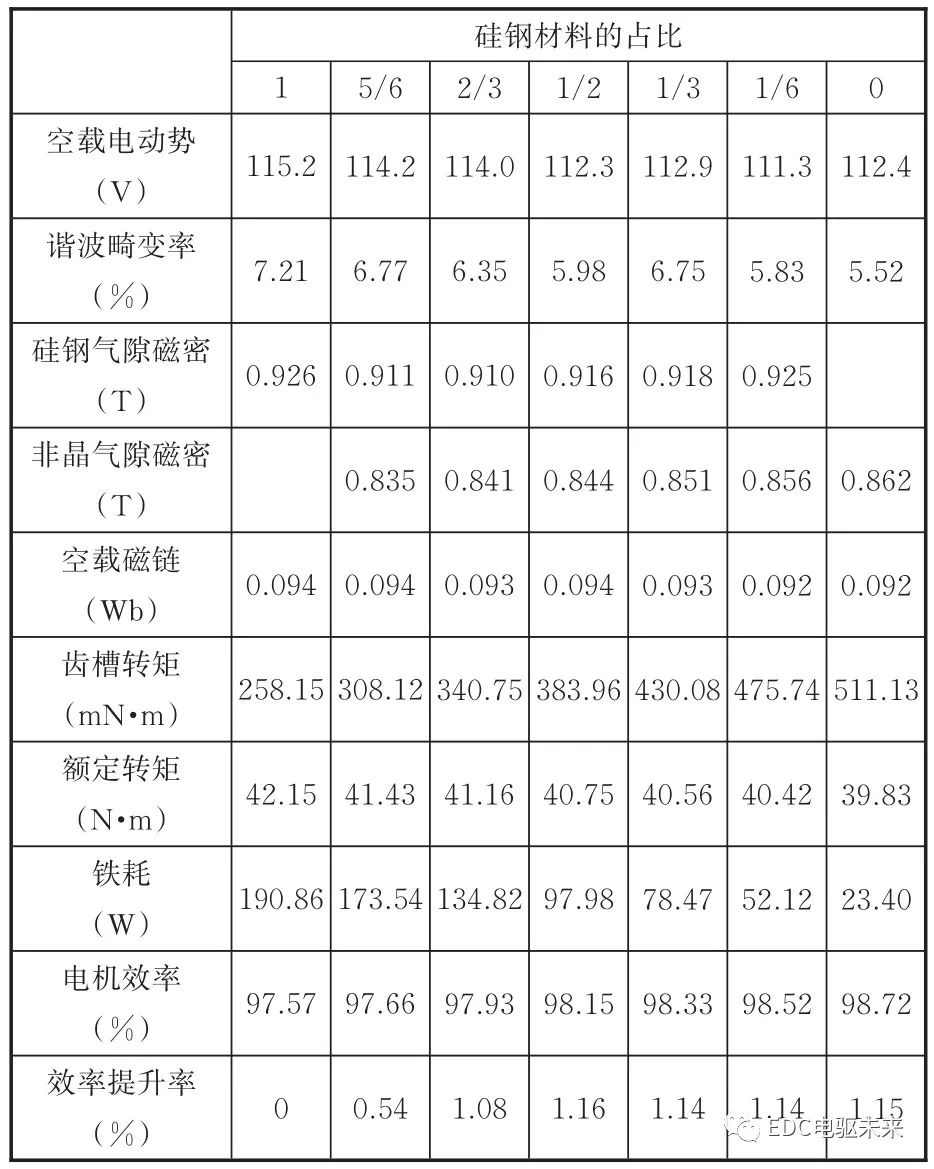
注：除輸出轉矩與鐵耗為平均值外，其余參數均為幅值。其中氣隙磁密為空載時電機氣隙中間位置處的磁密幅值；轉矩與鐵耗為額定工況下仿真所得的數據。

式中，Δη為電機的效率提升率；ηi為不同混合比例時電機的效率；ηn為純硅鋼電機的效率。

由計算結果得到不同比例下非晶合金對電機效率的提升率，見圖11。由圖11可見，隨著非晶合金比例的增大，電機效率的提升率增大，在非晶占比高于50%后，提升率趨于穩定。從再制造成本考慮，對于本款電機，非晶合金與硅鋼材料以1∶1比例混合較為合適。

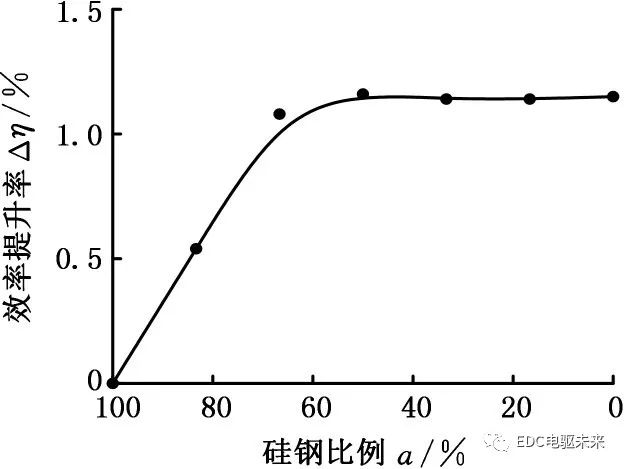
圖11 電機效率提升率
Fig.11 Efficiency improvement rate of motor

4.2 齒槽轉矩的分段斜槽優化

傳統的斜槽工藝中，通過將定子在整個軸向長度上傾斜不同的角度，以減少對應的齒諧波，達到減小齒槽轉矩的目的，但定子的傾斜角度不宜過大。基于分段疊加近似計算方法，本文提出了分段設置反向斜槽的方法，即對每段疊片段進行斜槽處理，通過減小每段疊片段的齒槽轉矩來減小整體的齒槽轉矩。分段反向斜槽示意圖見圖12。圖中豎直方向為電機軸向；粗實線表示沿軸向槽的傾斜方向與傾斜程度的變化；Ns表示每段的斜槽數。

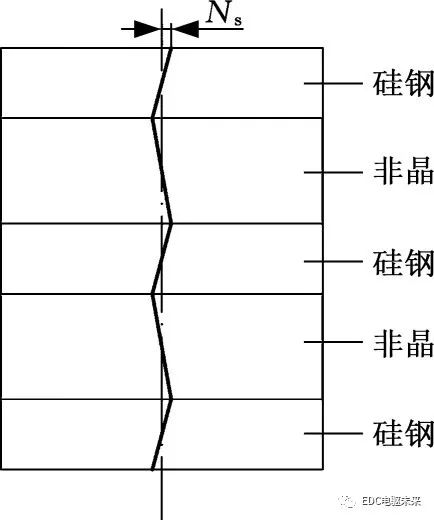
圖12 分段斜槽示意圖
Fig.12 Segmented reverse skewed slots diagram

通過多層分段二維有限元法，將每一段疊片段分為5層，每一層近似為直槽電機，通過設置不同的轉子初始角度模擬三維斜槽結構，并將仿真結果疊加，得到1∶1混合比例下正向斜槽與反向斜槽后電機的齒槽轉矩，見圖13。可以看出，正向斜槽時，當每段斜槽數為0.25與0.75時，齒槽轉矩的幅值較小，分別為25.05 mN·m與10.68 mN·m。這是因為，正向斜槽時，相同材料段間隔布置，其初始角度不同，對于8極48槽電機而言，齒槽轉矩的周期為一個槽距，當斜槽數為0.25的奇數倍時，相同材料段，尤其是非晶材料段的齒槽轉矩波形相差半個周期，出現了正負抵消的情況。反向斜槽時，隨著每段疊片段斜槽數的增大，齒槽轉矩幅值逐漸減小，當斜槽數為0.75時，齒槽轉矩幅值達到最小，為29.12 mN?m。

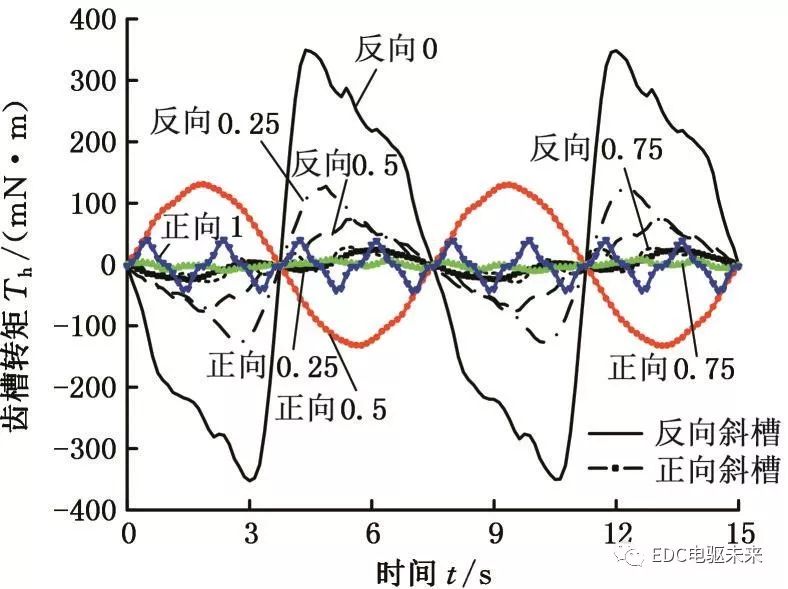
圖13 混合疊壓電機斜槽后的齒槽轉矩
Fig.13 The cogging torque after skewed of the hybrid electric motor

由圖13的分析可知，正向斜槽與反向斜槽都能有效減小電機的齒槽轉矩，在不考慮定子軸向總的傾斜角度時，正向斜槽的效果較好。定子斜槽時，尤其是正向斜槽時，若軸向總的傾斜角度過大，會對電機的電動勢造成較大的影響。選取正向斜槽數為0.25與0.75，反向斜槽數為0.75，通過分段二維有限元法，得到電機的電動勢，見圖14。其中原電機的空載電動勢幅值為115.20 V，諧波畸變率為7.21%。正向斜槽數為0.25和0.75時，電機的空載電動勢幅值分別為108.18 V和99.23 V；反向斜槽數為0.75時，電機的空載電動勢幅值為110.33 V；通過傅里葉分解計算空載電動勢的諧波畸變率，正向斜槽數為0.25、0.75與反向斜槽數為0.75時，電動勢諧波畸變率分別為5.30%、1.28%和4.16%。可見相比于原電機，斜槽后空載電動勢的諧波畸變率均得到一定優化，但當正向斜槽數為0.75時，空載電動勢相比原來明顯減小。反向斜槽數為0.75與正向斜槽數為0.25相比，齒槽轉矩略小，空載電動勢幅值較大，諧波畸變率較小，因此反向斜槽在有效減小電機齒槽轉矩的同時，能保證更好的電機性能。

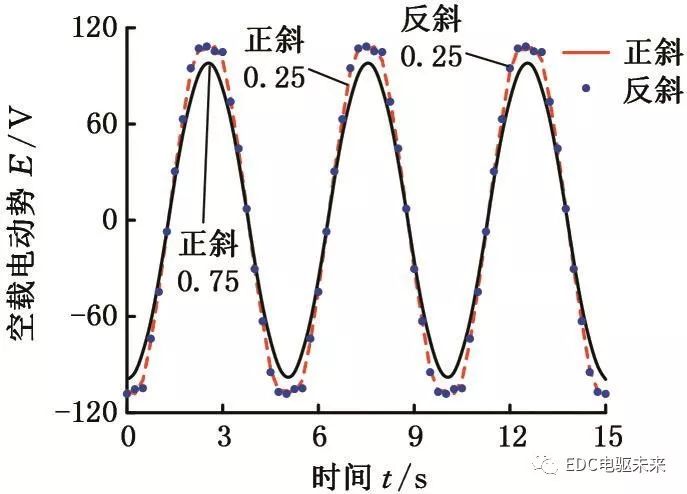
圖14 空載電動勢對比
Fig.14 Comparison of No-load EMF

5 結論

（1）基于能量法提出用二維分段疊加近似替代三維計算的定子混合疊壓電機齒槽轉矩計算方法，并通過仿真分析驗證了二維疊加近似計算混合疊壓電機齒槽轉矩的可行性，簡化了齒槽轉矩的優化分析。

（2）對比分析了不同混合比例下電機的各項性能參數。隨著非晶比例的增大，混合疊壓再制造電機的空載性能基本不變；額定工況下電機損耗降低、效率提高的同時，齒槽轉矩增大，輸出轉矩減小，電機效率提升率逐漸升高，當占比高于50%時趨于穩定；結合成本考慮，對于本款電機，選取再制造定子材料混合比例為1∶1。

（3）對正反斜槽后電機的齒槽轉矩與空載電動勢進行對比分析，正向斜槽對齒槽轉矩的減小效果更好，反向斜槽對空載電動勢幅值的影響較小；在確保空載電動勢幅值的情況下，對于本款電機，正向斜槽數為0.25與反向斜槽數為0.75時，電機的齒槽轉矩最小。

（4）對定子由純硅鋼和純非晶組成的電機齒槽轉矩進行了對比分析，研究了材料對齒槽轉矩的影響。定子采用非晶材料時齒槽轉矩的基波幅值大約是采用硅鋼材料時齒槽轉矩的基波幅值的4倍，其余各次諧波幅值相差不超過10 mN·m。定子材料對齒槽轉矩的影響主要體現在基波幅值上。

（5）仿真分析了不同混合疊壓方式下電機的齒槽轉矩。各次諧波幅值中最大差值約為11 mN·m，在一定的混合比例和總的分段數下，材料的分段數與混合疊壓順序對電機齒槽轉矩，即能量的變化規律影響較小。