摘要:
摘要: 標簽比例學習問題是一項僅使用樣本標簽比例信息去構建分類模型的挖掘任務,由于訓練樣本不充分,現有方法將該問題視為單一任務,在文本分類中的表現并不理想。考慮到遷移學習在一定程度上能解決訓練數據不充分的問題,于是如何利用歷史數據(原任務數據)幫助新產生的數據(目標任務數據)進行分類顯得異常重要。本文提出了一種基于標簽比例信息的遷移學習算法,將知識從原任務遷移到目標任務,幫助目標任務更好構建分類器。為了獲得遷移學習模型,該方法將原始優化問題轉換為凸優化問題,然后解決對偶優化問題為目標任務建立準確的分類器。實驗結果表明,大部分條件下所提算法性能優于傳統方法。
1. 引言
在傳統監督學習的分類問題中,已知所有樣本的標簽,分類器可以通過大量樣本屬性及其標簽學習得到,進而利用學習得到的分類器對未知標簽的樣本進行預測。但在實際應用中,通過人工標注獲取樣本標簽需要較高成本,或者受限于隱私等客觀條件,有時無法獲取所有樣本的標簽,而僅僅已知各類樣本的標簽比例信息,比如在匿名投票中,只能知道反對票和贊成票的比例。因此,在已知樣本標簽比例信息的前提下,以多個樣本組成的包為單位,基于包內樣本和包的標簽比例信息來訓練從而獲取樣本層面的分類器,更加具有實用價值。
近年來,標簽比例學習 [1] [2] (Learning with Label Proportions, LLP)在數據挖掘引起了廣泛的關注,并成功應用于現實生活中的許多領域,如欺詐識別、銀行重要客戶識別、垃圾郵件過濾、視頻事件檢測、收入預測、視覺特征建模等。在標簽比例學習問題中,只知道每個包中屬于不同類別的樣本的比例,但是樣本的標簽是未知的,它基于包層面的標簽比例信息解決了樣本層面的分類問題。
遷移學習(Transfer Learning) [3] [4] 是可以將知識從原任務(Source task)遷移到目標任務(Target task)的一種新的機器學習方法,其運用已存有的知識對不同但相關領域問題進行求解,遷移的知識可以幫助目標任務建立遷移學習分類器以進行預測。然而,大多數現有的方法都沒有考慮實踐中從原任務到目標任務的知識遷移,將標簽比例學習視為單一任務,無法解決遷移學習問題。
綜上所述,本文針對標簽比例學習問題,為了訓練得到更準確的分類器,提出了一種基于標簽比例信息的遷移學習算法(label proportion information-based transfer learning method, LPI-TL),該方法可以利用遷移學習將知識從原任務遷移到目標任務,幫助目標任務構建分類器。首先為了幫助目標任務學習預測模型,本文提出了一種遷移學習模型,然后使用拉格朗日方法將方法的原始問題轉換為凸優化問題并求解,最后獲得目標任務的預測分類器。實驗結果表明,本文方法在標簽比例問題上能取得更好的性能。
本文主要貢獻如下:
1) 結合支持向量回歸算法提出了基于標簽比例信息的遷移學習模型,該模型可以利用遷移學習將知識從原任務遷移到目標任務。
2) 利用拉格朗日方法將原始目標模型轉換為凸優化問題,并獲得原任務和目標任務的預測模型。
3) 在多個數據集上進行廣泛實驗,并與現有算法進行對比,驗證了提出算法的有效性。
2. 問題描述與相關工作
2.1. 問題描述
在標簽比例學習問題中,一個包內含有多個樣本,僅知道包中不同類別樣本的標簽比例信息。本文定義包的標簽比例為包中正樣本的比例。假設給定的原任務數據集為 D={x1,x2,?,xn}D={x1,x2,?,xn},則每個樣本xi所對應的標簽yi未知,數據會被分為t1個互相獨立的包 (BsI,PsI),I=1,2,?,ti(BIs,PIs),I=1,2,?,ti,其中 BsIBIs 和 PsIPIs 分別表示原任務數據集的第I個包和包中正樣本的比例 PsI=∣∣{xi∈BsI:yi=1}∣∣/∣∣BsI∣∣PIs=|{xi∈BIs:yi=1}|/|BIs|,同理,目標任務數據集用 (BtJ,PtJ),J=1,2,?,t2(BJt,PJt),J=1,2,?,t2 表示。
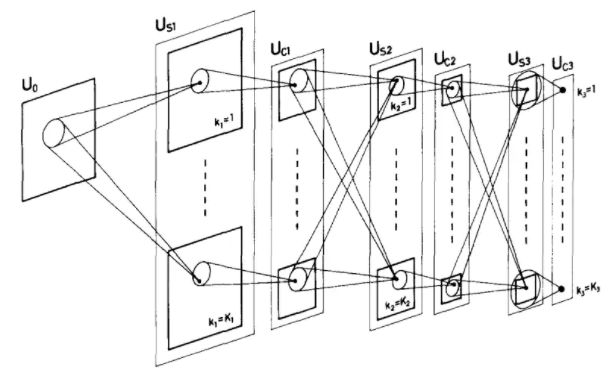
對于二元分類問題,標簽比例學習任務是學習一個分類器將未知標簽樣本分為正類或負類。如圖1所示:圖左邊的黑色橢圓表示包,黑色圓圈表示未標記的樣本。在圖的右邊,加號“+”和減號“?”分別表示分類后的正樣本和負樣本,實線表示由標簽比例和未標記的樣本訓練得到的分類器。
Figure 1. Two-class label proportions learning problem
圖1. 二分類標簽比例學習問題
2.2. 相關工作
本目前,國內外有多種標簽比例學習分類方法的研究,主要分為概率模型和支持向量機模型兩類。
基于概率模型的分類方法。文獻 [5] 假設給定類變量的預測變量之間具有條件獨立性,并采用了三種期望最大化算法來學習樸素貝葉斯模型。文獻 [6] 通過估計條件類密度來估計后驗概率,從貝葉斯角度提出一種新的學習框架,并且利用估計對數概率的網絡模型來求解分類問題的后驗概率。文獻 [7] 構建了一個應用于美國總統大選的概率方法,該方法使用基數勢在學習過程中對潛在變量進行推理,并引入了一種新的消息傳遞算法,將基數勢擴展到多變量概率模型。文獻 [8] 開發模型并使用Twitter數據來估算美國總統大選期間政治情緒與人口統計之間的關系。
基于支持向量機(Support Vector Machine, SVM)的分類方法。文獻 [9] 提出InvCal算法,該方法可以利用樣本的比例信息,反推出分類器,使得分類器預測出的樣本比例與實際比例相近。文獻 [10] 提出了Alter-SVM算法并通過交替優化的方法最小化損失函數。該方法在標準SVM模型的基礎上加入了比例損失的約束項,使得模型得到每個包的比例與實際比例盡可能接近。在文獻 [10] 的基礎上,文獻 [11] 提出了一種基于二支持向量機的分類模型,模型被轉換為兩個更小的二分類問題求解。文獻 [12] 首先分析了比例學習問題中的結構化信息,并利用數據點的幾何信息引入拉普拉斯項并且討論了如何將比例學習框架與拉普拉斯項結合。文獻 [13] 提出了一種基于非平行支持向量機的解決方案并將分類器改進為一對非平行分類超平面。
盡管對標簽比例學習的研究已經比較深入,然而大部分研究僅將該問題視為單一任務,沒有利用歷史數據彌補訓練樣本不充分的不足,不能很好地體現出分類器的效果。不同于大部分已有的工作,本文從遷移學習角度出發,利用遷移學習可以在相似領域中幫助新領域目標任務學習的特性,提出了一種基于標簽比例信息的遷移學習方法,該方法基于支持向量回歸方法并結合樣本組成的包構建模型,并給出了目標方程從而解決了遷移學習方法運用于標簽比例學習分類的問題。
3. 標簽比例學習算法
由于只通過標簽比例信息無法直接訓練分類函數,參考InvCal [9] 中利用標簽比例信息反推出分類器的操作,提出的方法使用Platt尺度函數 [14] 并反解求出y:
3.1. 目標函數
除對于具有相關性的原任務數據集和目標任務數據集,該算法使用f1和f2分別表示原任務和目標任務分類器:
其中 w1=w0+v1w1=w0+v1, w2=w0+v2w2=w0+v2,w0表示分離超平面的權向量公共參數,v1和v2為增量參數,原任務和目標任務越相似,則v1和v2越“小”,b1和b2是偏差。
本文對每個包中所有樣本求平均值得到一個平均數樣本來代表包,并利用支持向量回歸算法對所得到的平均數樣本求回歸方程,于是LLP問題轉換為求解如下目標函數:
其中: ξtiξti 和 ξ?ti(t=1,2)ξti?(t=1,2) 為訓練誤差, ε1iε1i 和 ε2mε2m 為可容忍損失,控制 εε 損失帶的大小;參數 λ1λ1 和 λ2λ2 用來控制原任務和目標任務權重,C1和C2是邊緣與經驗損失的權衡參數。
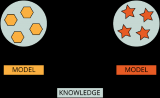
為了更好地理解遷移學習,圖2示意了知識遷移的基本思想。圖2中圓圈表示樣本,圓圈內數字表示樣本所屬包的編號,每個包都有兩個未知標簽的樣本,只知道包中正樣本的比例為50%;實線和虛線則分別表示分類器和間隔邊界。在圖的右邊,紅色圓圈表示目標任務樣本,當僅利用目標任務樣本構建分類。
Figure 2. Transfer knowledge from the source task to the target task
圖2. 原任務遷移知識到目標任務
3.2. 對偶問題
由于目標函數公式5為凸函數,引入拉格朗日乘子,公式5轉換為其對偶問題,等同為最小化下式:
具體算法求解過程如表1所示。
| 算法:LPI-TL |
|
輸入:?(?B?I?s?,?P?I?s?)?,?I?=?1?,?2?,???,?t?1?,?(?B?J?t?,?P?J?t?)?,?J?=?1?,?2?,???,?t?2?, λ?1?,?λ?2?,?C?1?,?C?2?,?ε 輸出:?w?1?,?w?2?,?b?1?,?b?2 方法: a):For i=1:(t1+t2) b):?y?i?=???log?(?1?p?i???1?) c): End d): 調用Matlab的CVX包求解公式6,解得拉格朗日乘子a e): 將a代入公式(7)-(9)求得w1,w2 f): 將w1,w2,yi代入公式3和公式4可解得b1,b2 |
Table 1. LPI-TL Algorithm
表1. LPI-TL算法流程
3.3. 時間復雜度分析
對于提出的LPI-TL算法,假設求解標準SVM的時間復雜度為 O([數據量]2)Ο([數據量]2),則在本文中解決公式6等同于求解一個數據量為M個原任務樣本和N個目標任務樣本的標準SVM問題,則最終的時間復雜度為 O((M+N)2)Ο((M+N)2)。
4. 實驗與分析
為驗證所提出算法的有效性,本文設計了數據實驗來驗證所述方法,并采用Inv-Cal [8],Alter-SVM [9] 和p-NPSVM [12] 作為對比方法。
4.1. 實驗數據
論本文采用SRAA1和20 Newsgroups2數據集,這兩個數據集是用于文本分類、文本挖掘和信息檢索研究的國際標準數據集之一,并被廣泛用于遷移學習實驗。SRAA數據集包含來自四個討論組的7327個UseNet文章,里面包含著模擬賽車,模擬航空,真實汽車,真實航空四個主題的數據。20 Newsgroups數據集收集了大約20,000左右的新聞組文檔,每個頂級類別下都有20個子類別,每個子類別都有1000個樣本。有一些新聞之間是相關的,比如Sci.elec vs. Sci.med;有一些新聞是不相關的,比如Sci.cryptvs.Alt.atheism。
由于上述兩個數據集不是專門為LLP問題設置,需要將文本數據集重新組織為適用于標簽比例學習問題的數據集。采用文獻 [15] [16] 處理上述數據集的方法,我們根據數據集的頂級類別重新組織LLP數據集。首先,我們從頂級類別(A)中選擇一個子類別a(1)作為正類別,因此將該子類別a(1)中的每個樣本視為正類樣本,其他頂級類別作為負類別。其次,對于原任務,我們從正子類別a(1)中隨機選擇多個樣本作為正樣本,并從其他類別中隨機選取相同數目的樣本作為負樣本,并將它們組成為原任務數據集。對目標任務執行相同的操作以形成正類樣本和負類樣本。為了使兩個任務相關,我們讓原任務和目標任務的正類具有相同的頂級類別,例如原任務為a(1),則目標任務為a(2)。在不損失有效性的情況下,我們僅保留具有較高文檔頻率的單詞以減少維數,并且每個樣本均由特征表示。最后隨機選取同等比例的正樣本和負樣本生成5個數據集,如表2所示。
| 編號 | 原任務 | 樣本個數 | 目標任務 | 樣本個數 |
| 1 | Simauto | 3000 | Realauto | 800 |
| 2 | Auto | 3000 | Aviation | 800 |
| 3 | Sci-elec | 5000 | Sci-med | 1500 |
| 4 | Rec.autos | 5000 | Rec.motor | 1500 |
| 5 | Spo.baseball | 5000 | Spo.hockey | 1500 |
Table 2. The list of data sets
表2. 數據集列表
4.2. 實驗設置
為減少包中樣本數量對實驗結果的影響,本實驗從每個數據集中分別隨機選擇20,40和60個樣本組成包,并分別對大小不同的包依次進行實驗,其中對四個算法的參數設置如下:
其中本文方法使用線性核函數 K(x1,x2)=x1?x2K(x1,x2)=x1?x2,采用五折交叉驗證法進行實驗。由于Inv-Cal,Alter-SVM和p-NPSVM為單一任務算法,對其只在目標數據集上進行實驗,對提出的算法則使用原任務數據集和目標任務數據集進行實驗。
4.3. 實驗結果分析
首先,利用本文提出的基于標簽比例信息的遷移學習算法遷移原任務數據知識來對目標任務數據集進行實驗,并采用準確率、精度、召回率和F1值等評價指標與Inv-Cal,Alter-SVM和p-NPSVM對比。
五個數據集具體的平均測試準確率和標準差實驗結果如表3所示。表3表明,在數據集3包的大小為20以及數據集4包的大小為40和60中,本文提出算法比其他方法略低外,在其他實驗結果中均能取得最高準確率和較低的標準差。圖3展示了這四個算法的平均準確率的柱狀圖,其中四個算法的平均準確率分別為:62.44%、63.09%、63.38%和67.77%,可見提出的算法LPI-TL的平均準確率高于Inv-Cal,Alter-SVM和p-NPSVM三個算法。這表明提出的方法在通過遷移原任務數據知識在分類準確率上能取得較高且穩定的性能。
另外,為了將其他算法與提出的LPI-TL方法進一步比較,將對上面實驗得到的準確率做Wilcoxon符號秩和檢驗 [17] [18]。通常,如果測試值p值低于置信度0.05,則LPI-TL與所比較的方法之間存在顯著差異。對于每種方法,其與LPI-TL之間的測試結果列在表4中。從表中可以看出,每種方法對LPI-TL的p值均小于置信度0.05,這意味著在統計視角中,本文提出的算法LPI-TL比其他三個方法在準確率上取得顯著性提高。
為了進一步驗證本文提出算法的性能,對5個數據集在包為20的情況下分別計算準確率、召回率和F1值等指標的平均值。實驗結果如表5所示。從表中可以看出,LPI-TL算法平均召回率比Alter-SVM算
| 數據集 | 算法 | 20 | 40 | 60 |
| 1 | Inv-Cal | 64.87 ± 1.60 | 60.42 ± 1.04 | 56.31 ± 2.00 |
| Alter-SVM | 62.53 ± 1.31 | 60.13 ± 1.20 | 60.72 ± 1.45 | |
| p-NPSVM | 66.72 ± 0.47 | 63.23 ± 0.96 | 60.02 ± 1.52 | |
| LPI-TL | 70.97 ± 0.37 | 68.60 ± 0.75 | 65.87 ± 1.22 | |
| 2 | Inv-Cal | 71.47 ± 0.70 | 68.37 ± 1.26 | 63.62 ± 1.06 |
| Alter-SVM | 70.03 ± 0.95 | 66.47 ± 0.97 | 63.03 ± 0.98 | |
| p-NPSVM | 71.30 ± 1.02 | 65.50 ± 1.11 | 65.31 ± 1.00 | |
| LPI-TL | 72.65 ± 0.41 | 72.57 ± 0.95 | 69.79 ± 0.82 | |
| 3 | Inv-Cal | 62.23 ± 0.73 | 59.52 ± 2.31 | 55.91 ± 1.79 |
| Alter-SVM | 60.52 ± 1.28 | 58.68 ± 1.45 | 56.76 ± 1.21 | |
| p-NPSVM | 63.22 ± 1.52 | 62.07 ± 1.35 | 57.82 ± 0.48 | |
| LPI-TL | 63.00 ± 0.73 | 64.32 ± 1.02 | 63.02 ± 0.75 | |
| 4 | Inv-Cal | 60.81 ± 1.47 | 62.02 ± 1.72 | 59.91 ± 1.79 |
| Alter-SVM | 64.07 ± 1.08 | 62.59 ± 0.93 | 60.06 ± 1.41 | |
| p-NPSVM | 61.19 ± 1.11 | 58.65 ± 1.03 | 56.02 ± 0.88 | |
| LPI-TL | 64.25 ± 0.92 | 62.03 ± 0.87 | 59.82 ± 0.75 | |
| 5 | Inv-Cal | 65.28 ± 1.32 | 63.56 ± 0.52 | 62.24 ± 1.24 |
| Alter-SVM | 70.32 ± 0.96 | 65.27 ± 0.76 | 65.21 ± 0.91 | |
| p-NPSVM | 68.02 ± 1.23 | 65.42 ± 1.04 | 66.13 ± 1.08 | |
| LPI-TL | 75.33 ± 0.62 | 73.56 ± 0.52 | 70.82 ± 0.53 |
Table 3. Experimental accuracy and standard deviation Statistics
表3. 實驗準確率和標準差結果統計
Figure 3. The mean accuracy
圖3. 平均準確率
| LPI-TL | R+ | R- | p-value |
| vs. Inv-Cal | 118 | 2 | 0.0062 |
| vs. Alter-SVM | 115 | 5 | 0.0144 |
| vs. p-NPSVM | 119 | 1 | 0.0380 |
Table 4. Wilcoxon signed ranks test.
表4. Wilcoxon符號秩和檢驗
| 算法 | 平均精度 | 平均召回率 | 平均F1值 |
| InvCal | 0.501 | 0.648 | 0.565 |
| Alter-SVM | 0.462 | 0.672 | 0.548 |
| p-NPSVM | 0.499 | 0.662 | 0.569 |
| LPI-TL | 0.554 | 0.667 | 0.606 |
Table 5. Performance comparison of each algorithm
表5. 各個算法性能對比
法低,這是由于Alter-SVM算法找出更多的負樣本,所以召回率更高;相比之下,LPI-TL算法取得更大的精度和F1值。總體來看,本文提出的LPI-TL算法的結果比對比方法更佳。
5. 結束語
本文對基于標簽比例信息的遷移學習進行了研究,為了目標任務能更有效的學習預測模型,本文提出了一種遷移學習的模型用于從標簽比例信息中學習分類器,該方法能將知識從原任務遷移到目標任務,并可以幫助目標任務構建分類器。本文實施了大量的實驗去研究該方法的性能,實驗表明該方法優于現有的LLP方法。該方法的不足之處在于僅能處理二分類問題還無法處理多分類數據,將來希望將該方法應用于多分類問題,這個問題值得后續進一步研究。
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App




























評論