人類的智能主要包括歸納主義和邏輯演繹,這兩大方面分別對應著人工智能中的聯結主義和符號主義。人類對大量低級信號的處理(如視覺信號以及聽覺信號)的感知處理都是下意識的,這便是基于大腦皮層神經網絡的學習方法;而大量數學公式的建立與推導,定理的證明具有強烈的主觀意識,是基于公里體系的符號演繹方法。
“1931年,天才數學家圖靈提出了著名的圖靈機模型,它奠定了人工智能的的基礎。1942年,麥克洛克和皮茨提出了著名的人工神經網絡模型,該模型一直沿用至今,它奠定了所有深度學習模型的基礎。神經網絡代表了一大類擅長并行計算的復雜系統,而圖靈機則代表了另一類以穿行方式計算的復雜系統。計算機之父馮諾伊曼已經指出,圖靈機和神經元本質上彼此等價,我們可以用圖靈機模擬神經元,亦可使用神經元模擬圖靈機。二者皆是圖靈完備的。
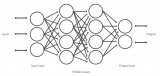
聯結主義的代表——神經網絡
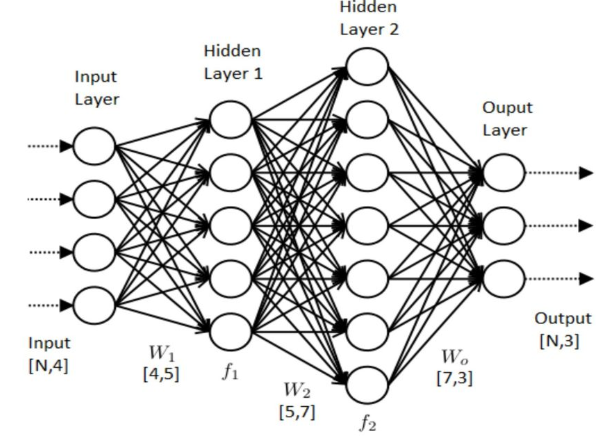
(帶有兩個隱層的人工神經網絡)人工神經網絡是一種借鑒了生物神經系統 神經網絡系統的計算模型,神經網絡由大量的人工神經元與神經元之間的突觸組成。神經網絡對輸入的信號進行層級加工,將最初的輸入信號進行特征提煉之后對特征進行組合學習。近幾年來,隨著算力和海量數據的積累,基于神經網絡的人工智能技術已經取得了前所未有的突破:在圖像識別領域最為先進的深度學習模型在某些模式識別領域取得的成果已然超過人類水平,使用深度對抗網絡的模型可以生成及其仿真的圖片。而在自然語言處理中,基于自注意力的transfomer模型更是將機器翻譯[1],文本生成等任務帶上了新的高度。另一方面,神經網絡的生物學基礎也得到了越來越多的支持,已有研究指出,基于卷機的神經網絡工作原理與視神經系統具有高度相似性,而另一些對于腦科學的研究已經揭示出了大腦對視覺和聽覺等信號的計算方式是通用的。這充分說明了以神經網絡為框架的人工智能的可行性。
雖然基于深度學習的人工智能取得了巨大的進步,但當前神經網絡面臨著巨大的問題,這些問題已然導致神經網絡即將走到其發展的瓶頸期。至今,還沒有準確且統一的數學模型可以完全解釋神經網絡的工作原理。缺乏理論框架導致對神經網絡研究缺乏目標性,神經網絡的研究進展逐漸放緩。以至于當今對神經網絡的研究大部分都集中在尋找更合適的超參數,或通過不同類型的神經網絡之間的組合來換取微小的精確度提高。今年,何凱明團隊實驗并發表了論文[2]:使用隨機連接構成的神經網絡依然可以有效的工作,這些隨機連接的神經網絡取得的結果甚至可以超過一些經過人工精心設計的網絡結構。不約而同的,谷歌大腦也在今年提出了不需要學習權重的神經網絡[3]。這兩篇論文都說明了必須尋找可解釋的神經網絡理論。
自動機理論
自動機是一種可以表示為數學模型的抽象計算機器,廣義上,不管是人工神經網絡還是圖靈機這類的計算模型都屬于自動機理論范疇。自動機可以用嚴格的數學語言描述:一般的有限狀態定向自動機被定義為一個五元組 (Q, A, G, S, F)。 其中符號Q被稱為自動機狀態的集合,A表示可以被自動機接受的符號集合,G是一組狀態轉換函數,其中的函數定義了自動機在接受特定的符號時,自動機會由當前狀態跳轉到下一個狀態。S被定義為自動機初始狀態的集合,而F被定義為自動機最終狀態的集合。給定輸入之后,自動機會根據當前狀態與狀態轉移函數進行自動計算。通過設計不同的狀態和狀態轉換函數,可實現對不同的系統的模擬。
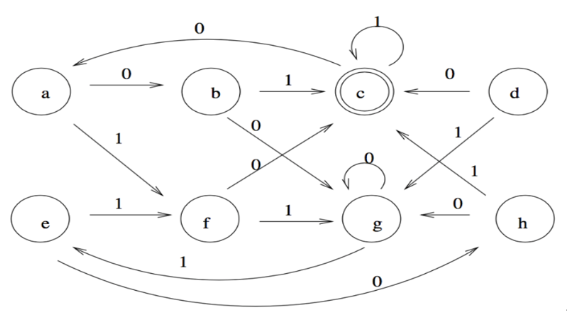
(具有8個狀態的有限自動機)自動機的背后有著嚴格的數學以及邏輯理論作為依靠。早在上世紀,學者們便開始嘗試設計各種不同的自動機模型來模擬智能,這些嘗試取得了非常令人驚訝的結果。計算機之父馮諾伊曼于40年代左右設計了被稱為元胞自動機的模型。元胞自動機是由一群簡單的小型自動機構成,這些小型自動機具有非常少的狀態以及簡單的狀態轉換函數,其特點是小型自動機的狀態轉換函數的輸入包括鄰居自動機的狀態,也就是說每一個小型自動機更新狀態的時候會受到來自其鄰居的影響。只要定義了自動機們的更新規則,元胞自動機便可不依靠外部力量自行完成演化。
元胞自動機系統的動力學演化背后隱藏的信息極其巨大。基于不同規則的元胞自動機展現出來的行為多種多樣,在馮諾伊曼之后對元胞自動機的研究揭示出了元胞自動機所能表示的系統遠遠超過我們的想象。Langton設計了一種可以通過改變一個全局參數來影響系統行為的元胞自動機。該全局參數如果過小,元胞自動機的行為便會非常簡單。參數值過大,元胞自動機的演化便會進入混沌[4]。Langton發現,在該參數位于某個值附近的時候,元胞自動機的動力學演化會位于一種所謂的“混沌邊緣”,此時系統展現出高度復雜但有序可循的模式。呈現出一種奇妙的自組織臨界狀態,無獨有偶,今年來自巴西的物理學家通過分析多種動物的大腦,也找到了大腦處于這種臨界狀態的新證據。這也從從另外一個角度間接證明了元胞自動機可以模擬復雜的智力系統。
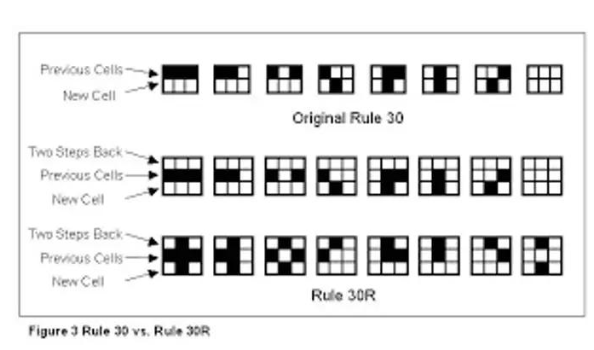
(元胞自動機狀態轉換規則示例)

(基于不同狀態轉換函數的元胞自動機演化結果)

(處在“混沌邊緣”的元胞自動機)上世紀50年代,前蘇聯數學家Tsetlin提出了可進行學習的自動機[5],此種類型的自動機可以通過從學習數據中改變自身的狀態轉換函數的概率來對數據進行學習。并可以使用自身的狀態來編碼信息,不同于神經網絡,這種自動機天然的具有對數據進行時序編碼的特性,且其具有良好的可解釋性。
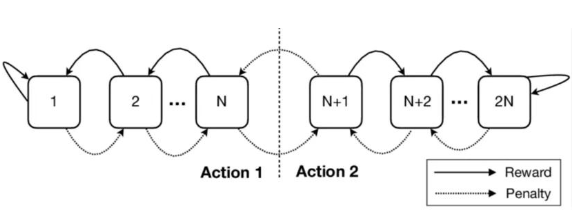
(Tsetlin學習自動機,其包含2N個狀態與兩個動作:懲罰與獎勵,通過設計狀態轉移函數調節兩個動作的行動概率,以此實現自Tsetlin提出學習自動機之后,人們逐漸意識到傳統自動機與概率論結合組成的學習自動機亦可對智能系統進行模擬。目前人工智能領域的專業雜志上出現了越來越多的使用可學習的自動機進行智能任務的論文,并取得了令人驚訝的結果。來自挪威阿格德爾大學的學者提出了一種基于Tsetlin學習自動機,并結合布爾邏輯的新型智能模型[6],該模型由簡單的Tsetlin學習自動機集群組成,使用布爾函數進行特征表達。該模型的訓練速度以及內存占用率是當前的神經網絡的數百分之一。
自動機在人工智能的潛力
自動機與傳統神經網絡的結合也可能是未來智能的趨勢。自動機是形式語言的數學模型,任何計算定理的證明或邏輯推理都可用自動機描述。而當下神經網絡在邏輯推理任務上的表現并不是很好,邏輯推理任務往往需要構建清晰的邏輯規則以及邏輯鏈,這恰恰是自動機語言所擅長的。今年,有團隊實驗了使用自動機來指導強化學習,將強化學習的子任務建模為自動機的狀態,并結合時序邏輯來建模子任務的相關性以及完成的先后順序,并以此規則來指導強化學習。不僅如此,來自馬里博爾大學的研究者在今年12月(2019年)發表了最新論文[7]:通過使用元胞自動機可以將不同種類的分類器組合成多重分類器(MCS),經過適當規則設計的元胞自動機可以自主的將各種機器學習方法得出的不同分類器組合到MCS中。并通過元胞自動機強大的自組織能力將特定的分類問題分配到對應的可以解決該問題的分類器上。
綜上,自動機與神經網路的結合展現出了巨大的潛力,一方面,自動機的背后有著嚴格的數學以及邏輯理論作為依靠,使其擁有良好的可解釋性。另一方面,自動機對于邏輯推理的建模是天然的,而神經網絡擅長對數據特征的提取,結合二者優勢的模型便可看作聯結主義與符號主義的結合。
未來的工作
1. 使用已發展的自動機理論來解釋指導當前人工神經網絡與強化學習的模型搭建,自動機理論已非常成熟,尋找當前神經網絡理論與自動機理論的結合點可使神經網絡的黑箱更加白化。極光無限正在研究將自動機與強化學習,滲透測試相結合,利用自動機的邏輯推斷,自動學習頂級滲透測試工程師們的攻擊路徑和攻擊模式,以達到全天候自動化滲透測試的目的。
2. 發掘并設計更多的自動機架構,融合到人工神經網絡結構中。各發揮所長:如使用神經網絡進行特征提取,使用自動機完成特征的組合與推斷。亦如利用自動機的內部狀態等信息進行輔助編碼,賦予神經網絡更強大的時序與記憶功能。
3. 設計專門的自動機網絡,以達到甚至取代當前神經網絡的目的。當前神經網絡有很多弊端,比如可解釋行,執行效率等,這些都可以通過自動機網絡得到解決。但是自動機網絡本身也有很多問題亟待解決,比如底層理論,訓練方式等等,我們相信未來的人工智能有自動機網絡的一席之地。
 電子發燒友App
電子發燒友App




















評論