在當(dāng)今世界中許多重要的數(shù)據(jù)集都以圖或網(wǎng)絡(luò)的形式出現(xiàn):社交網(wǎng)絡(luò)、知識圖表、蛋白質(zhì)交互網(wǎng)絡(luò)、萬維網(wǎng)等。然而直到最近,人們才開始關(guān)注將神經(jīng)網(wǎng)絡(luò)模型泛化以處理這種結(jié)構(gòu)化數(shù)據(jù)集的可能性。
目前其中有一些在專業(yè)領(lǐng)域中都得到了非常好的結(jié)果,在這之前的最佳結(jié)果都是由基于核的方法、基于圖論的正則化方法或是其他方法得到的。
大綱
神經(jīng)網(wǎng)絡(luò)圖模型的簡要介紹
譜圖卷積和圖卷積網(wǎng)絡(luò)(GCNs)
演示:用一個簡單的一階 GCN 模型進(jìn)行圖嵌入
將 GCNs 視為 Weisfeiler-Lehman 算法的可微泛化
如果你已經(jīng)對 GCNs 及其相關(guān)方法很熟悉了的話,你可以直接跳至「GCNs 第 Ⅲ 部分:嵌入空手道俱樂部網(wǎng)絡(luò)」部分。
圖卷積網(wǎng)絡(luò)到底有多強(qiáng)大
近期文獻(xiàn)
將成熟的神經(jīng)模型(如 RNN 或 CNN)泛化以處理任意結(jié)構(gòu)圖是一個極具挑戰(zhàn)性的問題。最近的一些論文介紹了特定問題的專用體系結(jié)構(gòu)。還有一些根據(jù)已知的譜圖理論構(gòu)建的卷積圖。
來定義在多層神經(jīng)網(wǎng)絡(luò)模型中使用的參數(shù)化濾波器,類似于我們所知且常用的「經(jīng)典」CNN。
還有更多最近的研究聚焦于縮小快速啟發(fā)式和慢速啟發(fā)式之間的差距,但還有理論更扎實(shí)的頻譜方法。Defferrard 等人(NIPS 2016,https://arxiv.org/abs/1606.09375)使用在類神經(jīng)網(wǎng)絡(luò)模型中學(xué)習(xí)得到的具有自由參數(shù)的切比雪夫多項(xiàng)式,在譜域中得到了近似平滑濾波器。他們在常規(guī)領(lǐng)域(如 MNIST)也取得了令人信服的結(jié)果,接近由簡單二維 CNN 模型得到的結(jié)果。
在 Kipf & Welling的文章中,我們采取了一種類似的方法,從光譜圖卷積框架開始,但是做了一些簡化(我們將在后面討論具體細(xì)節(jié)),這種簡化在很多情況下都顯著加快了訓(xùn)練時間并得到了更高的準(zhǔn)確性,在許多基準(zhǔn)圖數(shù)據(jù)集的測試中都得到了當(dāng)前最佳的分類結(jié)果。
GCNs 第 Ⅰ 部分:定義
目前,大多數(shù)圖神經(jīng)網(wǎng)絡(luò)模型都有一個通用的架構(gòu)。在此將這些模型統(tǒng)稱為圖卷積網(wǎng)絡(luò)(Graph Convolutional Networks,GCNs)。之所以稱之為卷積,是因?yàn)闉V波器參數(shù)通常在圖中所有位置(或其子集,參閱 Duvenaud 等人 2015 年發(fā)表于 NIPS 的文章共享。
這些模型的目標(biāo)是通過圖上的信號或特征學(xué)習(xí)到一個函數(shù)
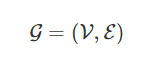
,并將其作為輸入:
每個節(jié)點(diǎn) i 的特征描述 x_i,總結(jié)為一個 N * D 的特征矩陣 X(N:節(jié)點(diǎn)數(shù)量,D:輸入特征數(shù)量)
圖結(jié)構(gòu)在矩陣形式中的一個代表性描述,通常以鄰接矩陣 A(或一些其他相關(guān)函數(shù))表示
之后會生成節(jié)點(diǎn)級輸出 Z(N * F 特征矩陣,其中 F 是每個節(jié)點(diǎn)的輸出特征的數(shù)量)。圖級輸出可以通過引入某種形式的池化操作建模。
然后每一個神經(jīng)網(wǎng)絡(luò)層都可以被寫成一個非線性函數(shù):

其中 H^(0)= X,H^(L)= Z(或?qū)?z 作為圖級輸出),L 是層數(shù)。模型的特異性僅表現(xiàn)在函數(shù) f( , ) 的選擇和參數(shù)化的不同。
GCNs 第 Ⅱ 部分:一個簡單示例
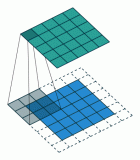
我們先以下述簡單的層級傳播規(guī)則為例:

式中 W(l) 是第 l 個神經(jīng)網(wǎng)絡(luò)層的權(quán)重矩陣,σ() 是一個非線性激活函數(shù)如 ReLU。盡管這個模型很簡單,但其功能卻相當(dāng)強(qiáng)大(我們稍后會談到)。
但是首先我們要明確該模型的兩個局限性:與 A 相乘意味著,對每個節(jié)點(diǎn)都是將所有相鄰節(jié)點(diǎn)的特征向量的加和而不包括節(jié)點(diǎn)本身(除非圖中存在自循環(huán))。我們可以通過在圖中強(qiáng)制執(zhí)行自我循環(huán)來「解決」這個問題——只需要將恒等矩陣添加到 A 上。
第二個局限性主要是 A 通常不是歸一化的,因此與 A 相乘將完全改變特征向量的分布范圍(我們可以通過查看 A 的特征值來理解)。歸一化 A 使得所有行總和為 1,即 D^-1 A,其中 D 是對角節(jié)點(diǎn)度矩陣,這樣即可避免這個問題。歸一化后,乘以 D^-1 A 相當(dāng)于取相鄰節(jié)點(diǎn)特征的平均值。在實(shí)際應(yīng)用中可使用對稱歸一化,如 D^-1/2 A D^-1/2(不僅僅是相鄰節(jié)點(diǎn)的平均),模型動態(tài)會變得更有趣。結(jié)合這兩個技巧,我們基本上獲得了 Kipf&Welling 文章中介紹的傳播規(guī)則:
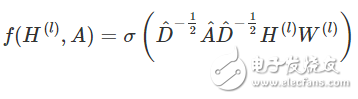
式中 A =A+I,I 是單位矩陣,D 是 A 的對角節(jié)點(diǎn)度矩陣。
在下一節(jié)中,我們將在一個非常簡單的示例圖上進(jìn)一步研究這種模型是如何工作的:Zachary 的空手道俱樂部網(wǎng)絡(luò)。
GCNs 第 Ⅲ 部分:嵌入空手道俱樂部網(wǎng)絡(luò)
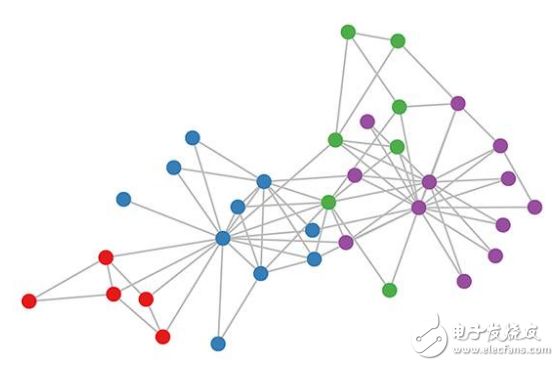
空手道俱樂部圖的顏色表示通過基于模塊化的聚類而獲得的共同體(詳情參閱 Brandes 等人發(fā)表于 2008 年的文章。
讓我們看一下我們的 GCN 模型是如何在著名的圖數(shù)據(jù)集上工作的:Zachary 的空手道俱樂部網(wǎng)絡(luò)(見上圖)。
我們采用了隨機(jī)初始化權(quán)重的 3 層 GCN。現(xiàn)在,即使在訓(xùn)練權(quán)重之前,我們只需將圖的鄰接矩陣和 X = I(即單位矩陣,因?yàn)槲覀儧]有任何節(jié)點(diǎn)特征)插入到模型中。三層 GCN 在正向傳遞期間執(zhí)行了三個傳播步驟,并有效地卷積每個節(jié)點(diǎn)的三階鄰域(所有節(jié)點(diǎn)都達(dá)到了三級「跳躍」)。值得注意的是,該模型為這些節(jié)點(diǎn)生成了一個與圖的共同體結(jié)構(gòu)非常相似的嵌入(見下圖)。到目前為止,我們已經(jīng)完全隨機(jī)地初始化了權(quán)重,并且還沒有做任何訓(xùn)練。
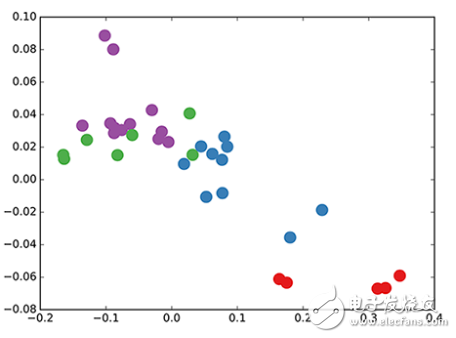
GCN 節(jié)點(diǎn)在空手道俱樂部網(wǎng)絡(luò)中的嵌入(權(quán)重隨機(jī))。
這似乎有點(diǎn)令人驚訝。最近一篇名為 DeepWalk 的模型(Perozzi 等人 2014 年發(fā)表于 KDD https://arxiv.org/abs/1403.6652)表明,他們可以在復(fù)雜的無監(jiān)督訓(xùn)練過程中得到相似的嵌入。那怎么可能僅僅使用我們未經(jīng)訓(xùn)練的簡單 GCN 模型,就得到這樣的嵌入呢?
我們可以通過將 GCN 模型視為圖論中著名的 Weisfeiler-Lehman 算法的廣義可微版本,并從中得到一些啟發(fā)。Weisfeiler-Lehman 算法是一維的,其工作原理如下 :
對所有的節(jié)點(diǎn)

求解鄰近節(jié)點(diǎn) {vj} 的特征 {h_vj}
通過 h_vi←hash(Σj h_vj) 更新節(jié)點(diǎn)特征,該式中 hash(理想情況下)是一個單射散列函數(shù)
重復(fù) k 步或直到函數(shù)收斂。
在實(shí)際應(yīng)用中,Weisfeiler-Lehman 算法可以為大多數(shù)圖賦予一組獨(dú)特的特征。這意味著每個節(jié)點(diǎn)都被分配了一個獨(dú)一無二的特征,該特征描述了該節(jié)點(diǎn)在圖中的作用。但這對于像網(wǎng)格、鏈等高度規(guī)則的圖是不適用的。對大多數(shù)不規(guī)則的圖而言,特征分配可用于檢查圖的同構(gòu)(即從節(jié)點(diǎn)排列,看兩個圖是否相同)。
回到我們圖卷積的層傳播規(guī)則(以向量形式表示):
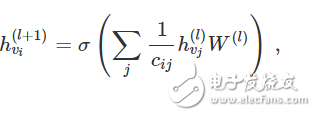
式中,j 表示 v_i 的相鄰節(jié)點(diǎn)。c_ij 是使用我們的 GCN 模型中的對稱歸一化鄰接矩陣 D-1/2 A D-1/2 生成的邊 (v_i,v_j) 的歸一化常數(shù)。我們可以將該傳播規(guī)則解釋為在原始的 Weisfeiler-Lehman 算法中使用的 hash 函數(shù)的可微和參數(shù)化(對 W(l))變體。如果我們現(xiàn)在選擇一個適當(dāng)?shù)摹⒎蔷€性的的矩陣,并且初始化其隨機(jī)權(quán)重,使它是正交的,那么這個更新規(guī)則在實(shí)際應(yīng)用中會變得穩(wěn)定(這也歸功于歸一化中的 c_ij 的使用)。我們得出了很有見地的結(jié)論,即我們得到了一個很有意義的平滑嵌入,其中可以用距離遠(yuǎn)近表示局部圖結(jié)構(gòu)的(不)相似性!
GCNs 的第 Ⅳ 部分:半監(jiān)督學(xué)習(xí)
由于我們模型中的所有內(nèi)容都是可微分且參數(shù)化的,因此可以添加一些標(biāo)簽,使用這些標(biāo)簽訓(xùn)練模型并觀察嵌入如何反應(yīng)。我們可以使用 Kipf&Welling文章中介紹的 GCN 的半監(jiān)督學(xué)習(xí)算法。我們只需對每類/共同體(下面視頻中突出顯示的節(jié)點(diǎn))的一個節(jié)點(diǎn)進(jìn)行標(biāo)記,然后開始進(jìn)行幾次迭代訓(xùn)練:
用 GCNs 進(jìn)行半監(jiān)督分類:用每類的一個單獨(dú)的標(biāo)簽進(jìn)行 300 次迭代訓(xùn)練得到隱空間的動態(tài)。突出顯示標(biāo)記節(jié)點(diǎn)。
請注意,該模型會直接生成一個二維的即時可視化的隱空間。我們觀察到,三層 GCN 模型試圖線性分離這些(只有一個標(biāo)簽實(shí)例的)類。這一結(jié)果是引人注目的,因?yàn)槟P筒]有接收節(jié)點(diǎn)的任何特征描述。與此同時,模型還可以提供初始的節(jié)點(diǎn)特征,因此在大量數(shù)據(jù)集上都可以得到當(dāng)前最佳的分類結(jié)果,而這也正是我們在文章中描述的實(shí)驗(yàn)所得到的結(jié)果。
結(jié)論
有關(guān)這個領(lǐng)域的研究才剛剛起步。在過去的幾個月中,該領(lǐng)域已經(jīng)獲得了振奮人心的發(fā)展,但是迄今為止,我們可能只是抓住了這些模型的表象。而神經(jīng)網(wǎng)絡(luò)如何在圖論上針對特定類型的問題進(jìn)行研究,如在定向圖或關(guān)系圖上進(jìn)行學(xué)習(xí),以及如何使用學(xué)習(xí)的圖嵌入來完成下一步的任務(wù)等問題,還有待進(jìn)一步探索。本文涉及的內(nèi)容絕非詳盡無遺的,而我希望在不久的將來會有更多有趣的應(yīng)用和擴(kuò)展。
 電子發(fā)燒友App
電子發(fā)燒友App











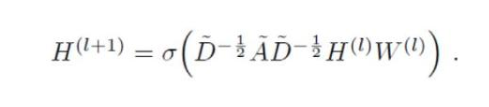
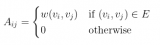













評論