最近,有一篇入門文章引發了不少關注。文章中詳細介紹了循環神經網絡(RNN),及其變體長短期記憶(LSTM)背后的原理。
具體內容,從前饋網絡(Feedforward Networks)開始講起,先后講述了循環神經網絡、時序反向傳播算法(BPTT)、LSTM等模型的原理與運作方式。
這篇文章來自Skymind,一家推動數據項目從原型到落地的公司。獲得了YCombinator、騰訊等的投資。
循環網絡,是一種人工神經網絡(ANN),用來識別數據序列中的模式。
比如文本、基因組、筆記、口語或來自傳感器、股票市場和政府機構的時間序列數據。
它的算法考慮了時間和順序,具有時間維度。
研究表明,RNN是最強大和最有用的神經網絡之一,它甚至能夠適用于圖像處理。
把圖像分割成一系列的補丁,可以視為一個序列。
但是,想要理解循環網絡,首先要必須了解前饋網絡的基本知識。
前饋網絡回顧
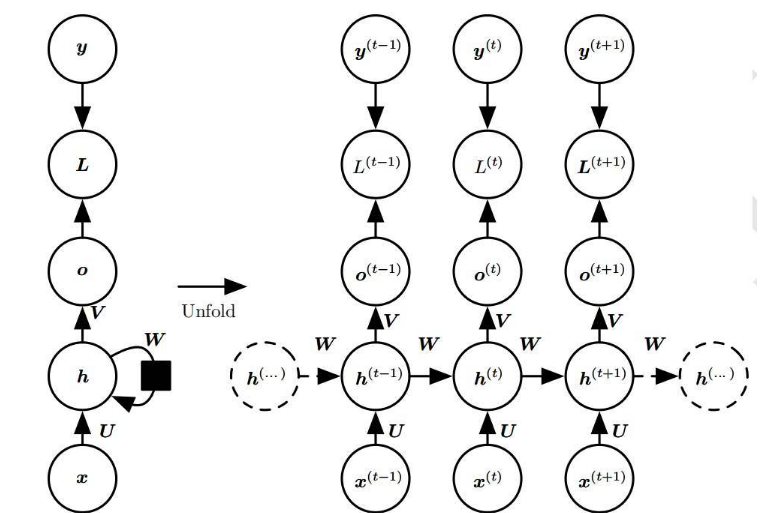
前饋網絡和循環網絡的命名,來自于它們在傳遞信息時,在網絡節點上執行的一系列數學運算的方式。
前饋網絡直接向前遞送信息(不會再次接觸已經經過的節點),而循環網絡則是通過循環傳遞信息。
前饋網絡中的樣例,輸入網絡后被轉換成輸出;在監督學習中,輸出將是一個標簽,一個應用于輸入的名稱。
也就是說,前饋網絡將原始數據映射到類別,識別出信號的模式。例如,輸入圖像應該被標記為“貓”還是“大象”。
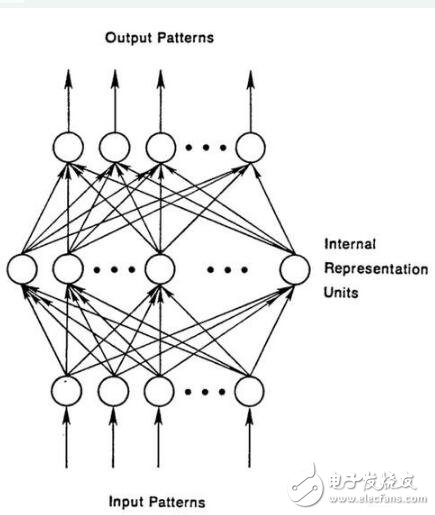
前饋網絡根據標記的圖像進行訓練,直到猜測圖像類別時產生的錯誤最小化。 通過一組經過訓練的參數(或者稱為權重,統稱為模型) ,網絡就可以對它從未見過的數據進行分類了。
一個訓練好的前饋網絡可以應用在任何隨機的照片數據集中,它識別的第一張照片,并不會影響它對第二張照片的預測。
看到一只貓的照片之后,不會導致網絡預下一張圖是大象。
也就是說,前饋網絡沒有時間順序的概念,它考慮的唯一輸入就是它所接觸到的當前的輸入樣例。
循環網絡
與前饋網絡相比,循環網絡的輸入不僅包括當前的輸入樣例,還包括之前的輸入信息。
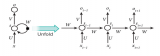
下面是美國加州大學圣地亞哥分校教授Jeffrey Elman提出的一個早期的簡單循環網絡的示意圖。
圖底部的BTSXPE代表當前時刻的輸入樣例,而CONTEXT UNIT代表前一時刻的輸出。
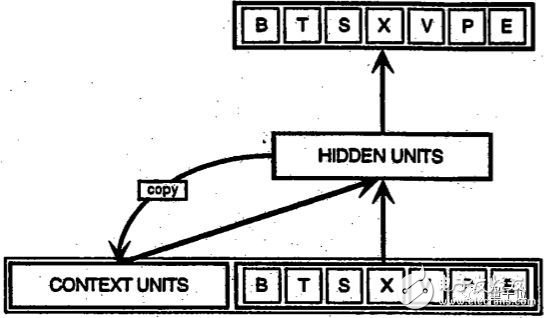
循環網絡在t-1個時間步的判定,會影響隨后在t時間步的判定。所以,循環網絡有兩個輸入源,現在和最近的過去,它們結合起來決定對新數據的反應,就像我們在生活中一樣。
循環網絡與前饋網絡的區別在于,循環網絡的反饋循環會連接到它們過去的判定,將自己的輸出作為輸入。
循環網絡是有記憶的。給神經網絡增加記憶的目的在于:序列本身帶有信息,循環網絡用它來執行前饋網絡不能執行的任務。
這些連續的信息被保存在循環網絡的隱藏狀態中,這種隱藏狀態管理跨越多個時間步,并一層一層地向前傳遞,影響網絡對每一個新樣例的處理。
循環網絡,需要尋找被許多時刻分開的各種事件之間的相關性,這些相關性被稱為“長距離依賴”,因為時間下游的事件依賴于之前的一個或多個事件,并且是這些事件的函數。
因此,你可以將RNN理解為是一種跨時間分享權重的方式。
正如人類的記憶在身體內無形地循環,影響我們的行為但不暴露全貌一樣,信息也在循環網絡的隱藏狀態中循環。
用數學的方式來描述記憶傳遞的過程是這樣的:
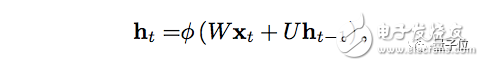
t代表時間步,ht代表第t個時間步的隱藏狀態,是同一個時間步xt的輸入函數。W是權重函數,用于修正xt。
U是隱藏狀態矩陣,也被稱為轉移矩陣,類似于馬爾可夫鏈。ht-1代表t的上一個時間步t-1的隱藏狀態。
權重矩陣,是決定當前輸入和過去隱藏狀態的重要程度的過濾器。 它們產生的誤差會通過反向傳播返回,并用于調整相應的權重,直到誤差不再降低。
權重輸入(Wxt)和隱藏狀態(Uht-1)的總和被函數φ壓縮,可能是邏輯S形函數或者是雙曲正切(tanh)函數,視情況而定。
這是一個標準工具,用于將非常大或非常小的值壓縮到邏輯空間中,并使梯度可用于反向傳播。
因為這個反饋循環發生在序列中的每個時間步中,每個隱藏狀態不僅跟蹤前一個隱藏狀態,只要記憶能夠持續存在,它會還包含h_t-1之前的所有的隱藏狀態。
給定一系列字母,循環網絡將使用第一個字符來幫助確定它對第二個字符的感知,比如,首字母是q,可能會導致它推斷下一個字母是u,而首字母是t,可能會導致它推斷下一個字母是h。
由于循環網絡跨越時間,用動畫來說明可能會更好。(可以將第一個垂直節點看作是一個前饋網絡,隨著時間的推移,它會變成循環網絡)。

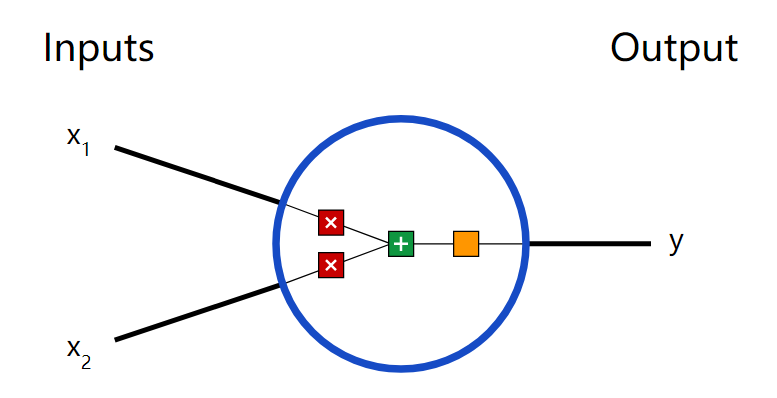
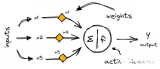
在上圖中,每個x是一個輸入樣例,w是過濾輸入的權重,a是隱藏層的激活(加權輸入和先前隱藏狀態的和),b是隱藏層使用修正線性或sigmoid單元轉換或壓縮后的輸出。
時序反向傳播算法(BPTT)
循環網絡的目的是準確地對序列輸入進行分類。主要依靠誤差的反向傳播和梯度下降法來做到這一點。
前饋網絡中的反向傳播從最后的誤差開始,經過每個隱藏層的輸出、權重和輸入反向移動,將一定比例的誤差分配給每個權重,方法是計算它們的偏導數?e/?w,或它們之間的變化率之間的關系。
隨后,這些偏導數會被用到梯度下降算法中,來調整權重減少誤差。
而循環網絡依賴于反向傳播的一種擴展,稱為時序反向傳播算法,即BPTT。
在這種情況下,時間通過一系列定義明確、有序的計算來表達,這些計算將一個時間步與下一個時間步聯系起來。
神經網絡,無論是循環的還是非循環的,都是簡單的嵌套復合函數,比如f(g(h(x))。添加時間元素,只是擴展了我們用鏈式法則計算導數的函數序列。
截斷式BPTT
截斷式BPTT(Truncated BPTT)是完整BPTT的近似方法,是處理是長序列的首選。
在時間步較多的序列中,完整BPTT的每個參數更新的正向/反向運算成本變得非常高。
截斷式BPTT的缺點是,由于截斷,梯度反向移動的距離有限,因此網絡無法學習與完整BPTT一樣長的依賴。
梯度消失和梯度爆炸
和大多數神經網絡一樣,循環網絡也有了一定的歷史。 到1990年代初,梯度消失問題成為影響網絡性能的主要障礙。
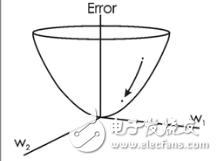
就像直線表示x的變化和y的變化一樣,梯度表示所有權重隨誤差變化的變化。如果我們不知道梯度,我們就不能在減少誤差的方向上調整權重,網絡也就會停止學習。
循環網絡,在最終的輸入和之前許多時間步之間建立聯系時,也遇到了問題。因為很難知道一個遠距離的輸入有多么重要。
就像向前追溯曾曾曾曾曾……祖父母兄弟的數量一樣,會越來越多,越來越多。
這在一定程度上是因為,通過神經網絡傳遞的信息要經過多個乘法階段。
每個研究過復利的人都知道,任何數量循環乘以略大于一的量,都會變得不可估量的大(實際上,簡單的數學真理支撐著網絡效應和社會不平等)。
反過來,乘以小于1的量,也會變得非常非常小。如果賭徒們每投入一美元,只能贏得97美分,那么他們很快就會破產。
由于深度神經網絡的層和時間步通過乘法相互關聯,導數很容易消失或爆炸。
梯度爆炸時,每一個權重就像諺語中的蝴蝶一樣,它拍打的翅膀會引起遠處的颶風。
但是梯度爆炸解決起來相對容易,因為它們可以被截斷或壓縮。
梯度消失正好相反,是導數變得非常小,使計算機無法工作,網絡也無法學習。這是一個更難解決的問題。
下面你可以看到一遍又一遍應用S形函數的效果。 數據曲線越來越平緩,直至在較長的距離上無法檢測到斜率。 這類似于通過許多層的梯度消失。
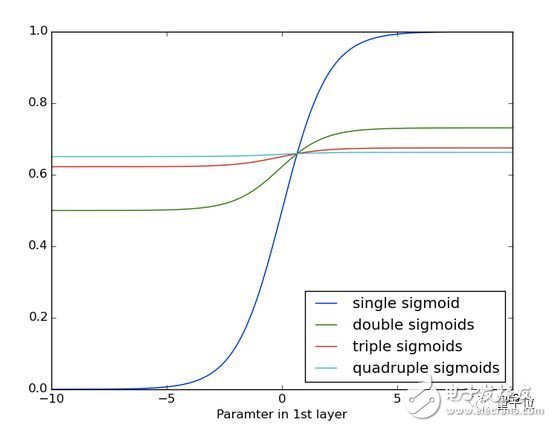
長短期記憶(LSTM)
在90年代中期,德國研究人員Sepp Hochreiter和Juergen Schmidhuber提出了一種具有長短期記憶單元( LSTM )的循環網絡變體,作為梯度消失問題的解決方案。
LSTM有助于保留可以通過時間和層進行反向傳播的誤差。
通過保留一個更為恒定的誤差,它們使循環網絡能夠在有許多時間步(超過1000步)的情況下繼續學習,從而打開一個遠程鏈接因果關系的通道。
這是機器學習和人工智能面臨的主要挑戰之一,因為算法經常遇到獎勵信號稀疏和延遲的環境。
LSTM將信息存放在循環網絡正常信息流之外的門控單元中。信息可以像計算機內存中的數據一樣存儲、寫入單元,或者從單元中讀取。
單元通過打開和關閉的門來決定存儲什么,以及何時允許讀取、寫入和忘記。
但與計算機上的數字存儲器不同,這些門是模擬的,通過范圍在0~1之間的sigmoid函數的逐元素相乘來實現。
與數字信號相比,模擬信號的優勢是可微分,因此適用于反向傳播。
這些門類似于神經網絡的節點,會根據它們接收到的信號決定開關,它們根據信息的強度和重要性來阻止或傳遞信息,然后用它們自己的權重過濾這些信息。
這些權重,就像調整輸入和隱藏狀態的權重一樣,可以在循環網絡學習過程中進行調整。
也就是說,記憶單元學習會通過猜測、反向傳播誤差和梯度下降法調整權重的迭代過程,來決定何時允許數據進入、離開或刪除。
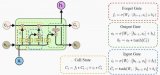
下圖說明了數據如何通過記憶單元,以及門如何控制數據流動。
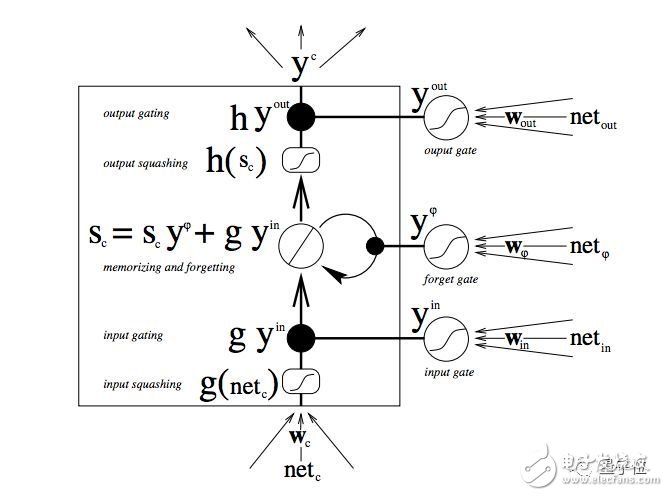
如果你剛剛接觸LSTM,不要著急,仔細研究一下。只需要幾分鐘,就能揭開其中的秘密。
從底部開始,三個箭頭顯示,信息由多個點流入記憶單元。 當前輸入和過去單元狀態的組合不僅反饋到單元本身,而且反饋到它的三個門中的每一個,這將決定它們如何處理輸入。
黑點是門本身,決定是否讓新的輸入進入、遺忘當前的狀態,還是讓這一狀態在當前時間步影響網絡的輸出。
Sc是記憶單元的當前狀態,g_y_in是記憶單元的當前輸入。
請記住,每個門都可以打開或關閉,它們會在每一步重新組合它們的打開和關閉狀態。記憶單元,在每個時間步都可以決定,是否遺忘、寫入、讀取它的狀態,這些流都表示出來了。
大的、加粗的字母,給出了每個操作的結果。
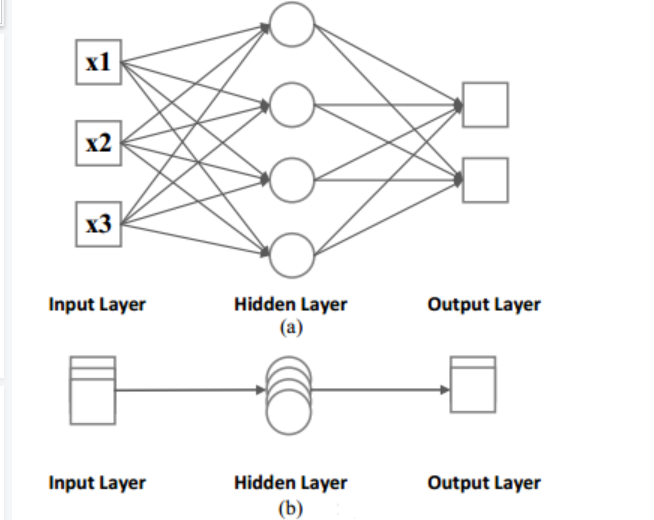
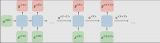
下面是另一個示意圖,對比了簡單的循環網絡(左)和 LSTM 單元(右)。
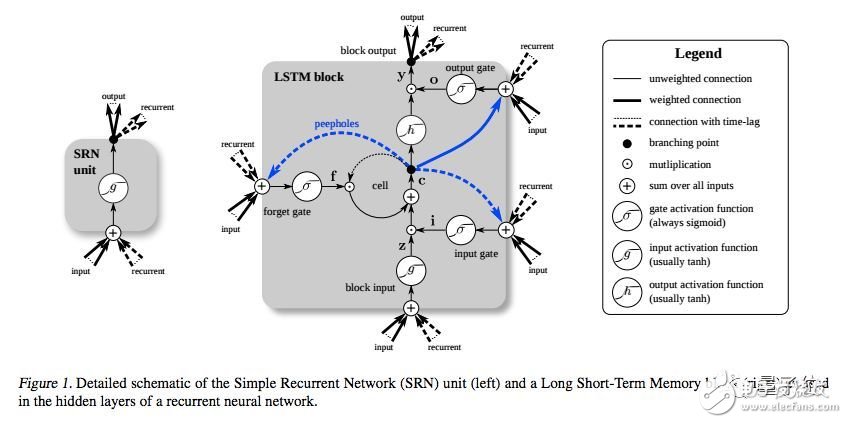
值得注意的是,LSTM的記憶單元在輸入轉換中賦予加法和乘法不同的角色。
兩個圖中的中心加號,本質上就是 LSTM 的秘密。
雖然這看起來非常非常簡單,但當必須在深度上反向傳播時,這種變化有助于保持恒定的誤差。
LSTM不是將當前狀態乘以新的輸入來確定后續的單元狀態,而是將兩者相加,這就產生了差異。 (用于遺忘的門仍然依賴于乘法。)
不同的權重集對輸入信息進行篩選,決定是否輸入、輸出或遺忘。
不同的權重集對輸入信息進行過濾,決定是否輸出或遺忘。遺忘門被表示為一個線性恒等式函數,因為如果門是打開的,那么記憶單元的當前狀態就會被簡單地乘以1,從而向前傳播一個時間步。
此外,有一個簡單的竅門。將每個LSTM記憶單元遺忘門的偏差設定為1,可以提升網絡性能。(但另一方面,Sutskever建議將偏差設定為5。)
你可能會問,LSTM的目的是將遠距離事件與最終的輸出聯系起來,為什么它們會有一個遺忘門?
好吧,有時候遺忘是件好事。
如果分析一個文本語料庫,在到達一個文檔的末尾時,下一個文檔基本上跟它沒有關系,因此,在網絡攝取下一個文檔的第一個元素之前,應該將記憶單元設置為零。
以分析一個文本語料庫為例,在到達文檔的末尾時,你可能會認為下一個文檔與這個文檔肯定沒有任何聯系,所以記憶單元在開始吸收下一個文檔的第一項元素前應當先歸零。
在下圖中,你可以看到在工作的門,直線表示關閉的門,空白圓圈代表打開的門。沿著隱藏層水平延伸的線條和圓圈是表示遺忘門。

需要注意的是,前饋網絡只是一對一,即將一個輸入映射到一個輸出。但循環網絡可以一對多,多對多,多對一。
涵蓋不同時間尺度和遠距離依賴
你可能還想知道,保護記憶單元不受新數據進入的輸入門和防止它影響 RNN 的某些輸出的輸出門的精確值是多少。你可以把 LSTM 看作是,允許一個神經網絡同時在不同的時間尺度上運行。
讓我們以一個人的生命為例,想象一下我們在一個時間序列中收到了關于那個生命的各種數據流。
每個時間步的地理位置,對于下一個時間步來說都非常重要,因此時間尺度總是對最新信息開放的。
也許這個人是一個勤奮的公民,每兩年投票一次。在民主時代,我們會特別關注他們在選舉前后的所作所為。我們不想讓地理位置持續產生噪音影響我們的政治分析。
如果這個人也是一個勤奮的女兒,那么也許我們可以構建一個家庭時間,學習每周日定期打電話的模式,每年假期前后,打電話的數量都會激增。這與政治周期或地理位置無關。
其他的數據也是這樣。音樂是多節奏的。文本中包含不同時間間隔的重復主題。股票市場和經濟會有更長的波動周期。它們在不同的時間尺度上同時運行,LSTM可以捕捉到這些時間尺度。
門控循環單元(GRU)
門控循環單元( GRU )基本上是沒有輸出門的LSTM,因此在每個時間步,它都將內容從其記憶單元完全寫入到較大的網絡中。
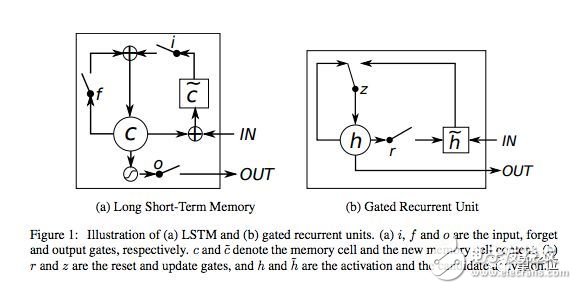
代碼示例
這里示例,是一個LSTM如何學習復制莎士比亞戲劇的評論,使用Deeplearning4j實現。在難以理解的地方,都有相應的注釋。
傳送門:
https://github.com/deeplearning4j/dl4j-examples/blob/master/dl4j-examples/src/main/java/org/deeplearning4j/examples/recurrent/character/LSTMCharModellingExample.java
LSTM超參數調整
以下是手動優化RNN超參數時需要注意的一些情況:
小心過擬合,神經網絡基本在“記憶”訓練數據時,就會發生過擬合。過擬合意味著你在訓練數據上有很好的表現,在其他數據集上基本無用。
正則化有好處:方法包括 l1、 l2和dropout等。
要有一個單獨的測試集,不要在這個測試集上訓練網絡。
網絡越大,功能就越強,但也更容易過擬合。 不要試圖從10000個示例中學習一百萬個參數,參數》樣例=麻煩。
數據越多越好,因為它有助于防止過度擬合。
訓練要經過多個epoch(算法遍歷訓練數據集)。
每個epoch之后,評估測試集表現,以了解何時停止(要提前停止)。
學習速率是最重要的超參數。
總體而言,堆疊層會有幫助。
對于LSTM,可以使用softsign(而不是softmax)函數替代雙曲正切函數,它更快,更不容易飽和( 梯度大概為0 )。
更新器:RMSProp、AdaGrad或Nesterovs通常是不錯的選擇。AdaGrad也會降低學習率,這有時會有所幫助。
記住,要將數據標準化、MSE損失函數+恒等激活函數用于回歸、Xavier權重初始化。
 電子發燒友App
電子發燒友App











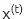

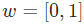














評論